Volume Benda Putar [Aplikasi Integral]

Aplikasi Integral: Volume Benda Putar

Pembahasan soal-soal Ujian Nasional (UN) bidang studi Matematika SMA-IPA dengan materi pembahasan Volume Benda Putar (aplikasi integral) yang meliputi volume benda putar terhadap sumbu x dan sumbu y.

Soal tentang Volume Benda Putar UN 2012

Pembahasan

Batas integrasi daerah putar tersebut adalah titik potong antara kurva y₁ = x² dan garis y₂ = 2x. Titik potong dapat dicari dengan menyamakan kedua fungsi tersebut.

         y₁ = y₂
         x² = 2x
 x² − 2x = 0
x(x − 2) = 0
x₁ = 0 dan x₂ = 2

Perhatikan gambar berikut ini!

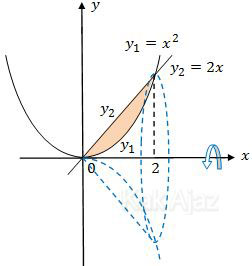
Pada daerah yang diarsir, y₂ > y₁ sehingga fungsi yang diintegral adalah:

y₂² − y₁²

Dengan demikian, volume benda putar tersebut adalah:

Kita hanya perlu memasukkan batas x=2 saja. batas x=0 tidak perlu dimasukkan karena akan menghasilkan nol.

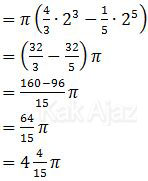
Jadi, volume benda putar tersebut adalah 4 4/15 π satuan volume (C).

Soal tentang Volume Benda Putar UN 2013

Pembahasan

Kita tentukan dulu batas-batasnya.

y₁ = y₂
x² + 1 = x + 3
x² − x − 2 = 0
(x + 1)(x − 2 ) = 0
x₁ = −1 dan x₂ = 2

Parabola y₁ = x² + 1 terbuka ke atas (karena koefisien x²-nya positif). Oleh karena itu dapat dipastikan parabola tersebut terletak di bawah garis y₂ = x + 3.

Sehingga fungsi yang diintegral adalah:

y₂² − y₁² = (x + 3)² − (x² + 1)²
               = x² + 6x + 9 − (x⁴ + 2x² + 1)
               = −x⁴ − x² + 6x + 8

Dengan demikian, volume benda putar tersebut adalah:

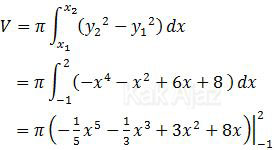
Batas-batasnya kita masukkan per suku seperti berikut ini:

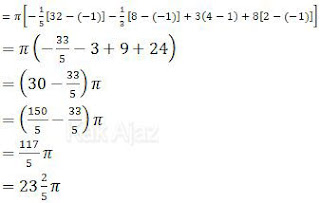
Jadi, volume benda putar tersebut adalah 23 2/5 π satuan volume (D).

Soal tentang Volume Benda Putar UN 2015

Pembahasan

Titik potong kurva y = 4 − x² pada sumbu x adalah:

                   y = 0
           4 − x² = 0
(2 − x)(2 + x) = 0
x = −2 dan x = 2

Perhatikan gambar berikut ini!

Daerah yang diarsir berada pada kuadran I, dibatasi oleh kurva, sumbu x, dan sumbu y. Daerah tersebut kemudian diputar 360° terhadap sumbu x. Volume yang terjadi adalah:

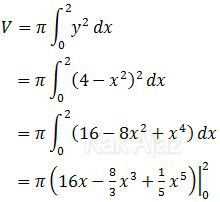
Masukkan batas x = 2 saja.

Jadi, volume benda putar tersebut adalah 256/15 π satuan volume (B).

Soal tentang Volume Benda Putar UN 2011

Pembahasan

Titik potong antara kurva y₁ = x² dan garis y₂ = 2x adalah:

y₁ = y₂
x² = 2x
x² − 2x = 0
x(x − 2) = 0
x₁ = 0 dan x₂ = 2

Karena kurva y₁ terbuka ke atas maka posisinya berada di bawah garis y₂. Sehingga volume benda putar yang terjadi adalah:

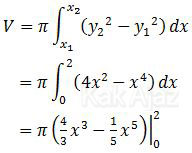
Dengan memasukkan batas x = 2 diperoleh:

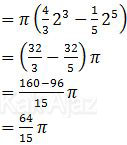
Jadi, volume benda putar yang terjadi adalah 64/15 π satuan volume (D).

Soal tentang Volume Benda Putar UN 2014

Pembahasan

Soal ini agak berbeda dengan soal sebelumnya. Hal ini karena benda tersebut diputar terhadap sumbu y (soal sebelumnya diputar terhadap sumbu x).

Karena diputar terhadap sumbu y maka batas integrasi adalah batas y, yaitu y₁ dan y₁.

Ok, kita substitusikan persamaan kurva x = 2√3 y² pada lingkaran x² + y² = 1 untuk mendapatkan batas-batas integrasinya.

                 x² + y² = 1
     (2√3 y² )² + y² = 1
             12y⁴ + y² = 1
       12y⁴ + y² − 1 = 0
(4y² − 1)(3y² + 1) = 0
y² = 1/4 dan y² = −1/3 (TM)
y = ±1/2

TM artinya tidak memenuhi karena hasil pengkuadratan tidak mungkin bernilai negatif.
Perhatikan gambar berikut ini!

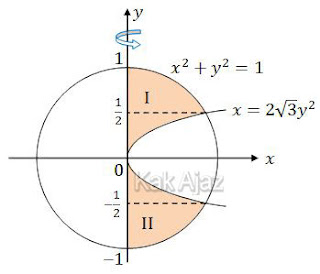
Daerah yang diarsir dibatasi oleh kurva, lingkaran, dan sumbu y. Daerah inilah yang akan diputar 360° terhadap sumbu y.

Daerah I dan II pada arsiran di atas luasnya sama besar. Sehingga kita cukup mengintegralkan daerah I saja kemudian kita kalikan 2.

Sementara itu, daerah I tidak bisa kita integralkan langsung dari y = 0 ke y = 1. Melainkan harus dipecah menjadi dua.

Dalam interval 0 ≤ y ≤ 1/2 yang berperan adalah kurva parabola. Sedangkan dalam interval 1/2 ≤ y ≤ 1 yang berperan adalah lingkaran.

Yang perlu ditekankan lagi adalah bahwa fungsi yang diintegral adalah fungsi x² sehingga:

Parabola:    x = 2√3 y²
                 x² = 12y⁴

Lingkaran :  x² + y² = 1
                           x² = 1 − y²

Dengan demikian, Volume benda putar tersebut adalah:

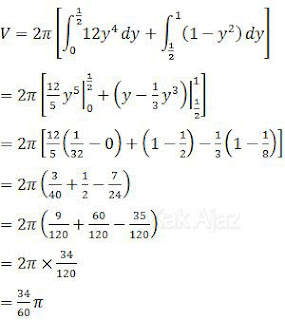
Jadi, volume benda putar tersebut adalah 34/60 π satuan volume (C).

Pembahasan soal Volume Benda Putar yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 35
Pembahasan Matematika IPA UN 2014 No. 35
Pembahasan Matematika IPA UN 2015 No. 37

Simak juga:
Pembahasan Matematika IPA UN: Luas Daerah [Aplikasi Integral]
Pembahasan Matematika IPA UN: Integral Fungsi Aljabar.
Pembahasan Matematika IPA UN: Integral Fungsi Trigonometri

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih