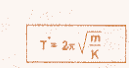Pembahasan Selanjutnya
GERAK HARMONIK SEDERHANA dan GETARAN
Fisika sekolah madrasah blog
⧪ Getaran Pegas

T = periode getaran pegas
M = massa beban
K = konstanta pegas
K = ω2. m
ω
= 2 π f
f = frekuensi getaran
⧪ Bandul
Sederhana

T = periode getaran bandul
l = panjang bandul
g = percepatan gravitasi
⧪ Getaran
Selaras Rotasi pada katrol

k = koefisien momen
inersia katrol
⧪ Persamaan umum Simpangan

y = simpangan
ω = 2 π f
f = frekuensi getaran

v = kecepatan
ω = 2 π f
f = frekuensi getaran
Getaran Selaras
a = percepatan (m/s)
⧪ Energi getaran Selaras
:
–
Energi Kinetik
Ek = 1/2 mv2
Ek = 1/2 KA2 cos2wt
Ek =
enenrgi kinetik
–
Energi Potensial
Ep = 1/2 ky2
Ep = 1/2 KA2 sin2wt
Ep = energi potensial
–
Energi Mekanik
Em = Ek + Ep
Em = 1/2 KA2
⧪ Rumus dan konsep tambahan (aplikasi dalam soal)
–
Mencari Ep, Ek, a, y dan v
bandul saat berada di titik kesetimabangan dan saat simpangan maksimum:

–
Mencari v (kecepatan) jika
diketahui y (simpangan
⧪ Contoh soal dan pembahasan pilihan ganda:
1.
Benda
yang massanya 400 gram melakukan gerakan harmonik dengan persamaan simpangan y
= 0,05 sin 100t. Jika y dan t dalam meter dan sekon, maka energi getaran dari
gerak harmonik tersebut adalah …
A. 50 Joule D. 10 Joule
B. 40 Joule E. 5 Joule
C. 20 Joule
Pembahasan:
Energi getaran sama dengan energi mekanik:
EM = ½ k A2 = ½ ω2
. m . A2
EM = ½ . 1002 . 0,4 . 0,052 = 20 joule
Jadi, jawabanya C
2.
Sebuah
ayunan sederhana, panjang tali 100 cm massa benda 100 gram, percepatan
gravitasi 10 m/s2. Kedudukan tertinggi 20 cm dari titik terendah.
Maka kecepatan berayunnya pada titik terendah adalah ……
A. 40 m/s
B. 20 m/s
C. 4 m/s
D. 2 m/s
E. 0,2 m/s
Jawab:
Pembahasan:
Soal seperti ini dapat diselesaikan dengan energi mekanik atau dengan
pendekatan gerak jatuh bebas, karena yang mempengaruhi gerak bandul kebawah
hanya percepatan gravitasi.
– Cara 1 (gerak jatuh bebas)
V2 = 2gh = 2 . 10 . 0,2
V2 = 4
V = 2 m/s
3.
Sebuah
partikel bergerak harmonik dengan amplitudo 13 cm dan periodenya 0,1 π sekon.
Kecepatan partikel pada saat simpangannya 5 cm adalah ……
A. 2,4 m/s
B. 2,4 π m/s
C. 2,4 π2
m/s
D. 24 m/s
E. 240 m/s
Pembahasan:
4.
Jika
sebuah gerak harmonik memiliki persamaan gerak y = 0,10 sin 20 πt, maka
besarnya frekuensi benda tersebut adalah……
A. 0,1 Hz D. 20 Hz
B.
1,0
Hz E. 20,1
Hz
C.
l0
Hz
pembahasan:
y = 0,10 sin 20 πt

ω = 2 π f
20π = 2 π f
f = 10 Hz
5. Sebuah benda bergetar harmonik sederhana dengan frekwensi 10 Hz. Setelah 25 s, benda bergetar….
A. 250 kali
B. 25 kali
C. 2/5 kali
D. ¼ kali
E. 1/8 kali
jawab:
pembahasan:
f = n/t
n = f.t
n = 10 . 25 = 250 kali
6. Sebuah pegas dengan konstanta 400 N/m digantung pada statis dimana ujung bebas digantungkan beban sebesar 4 kg. Besar frekwensi getaran pegas tersebut adalah….
A. 5π Hz
C. 5 Hz
D. 10π Hz
E. 10/π Hz
jawab:
pembahasan:
rumus frekuensi pegas
k = 𝜔2.m
400 = (2πf)2 . 4
100 = (2πf)2
10 = 2πf
5 = πf
f = 5/π
7. Sebuah partikel bergerak harmonic dengan periode 0,1 s dan amplitude 1 cm. Pada saat berada jarak patikel 0,6 cm dari titik kesetimbangan, Kelajuan partikel tesebut adalah…
A. 4π cm/s
B. 8π cm/s
C. 16π cm/s
D. 8 cm/s
E. 16 cm/s
jawab:
pembahsan:
f = 1/T
f = 1/0,1
f = 10 Hz
v2 = (2πf)2 . (A2 – y2)
v2 = (2π10)2 . (12 – 0,62)
v2 = (20π)2 . (1 – 0,36)
v2 = (20π)2 . (0,64)
v = (20π) . (0,8)
v = 16π
8. Sebuah benda melakukan getaran harmonic sederhan dengan persamaan simpangan y =(10 sin (πt)) cm. Besar kecepatan getaran benda setelah ¼ detik adalah…
A. -10π√(2 ) cm/s
B. -10π cm/s
C. -5π√(2 ) cm/s
D. 5π√(2 ) cm/s
E. 10π√(2 ) cm/s
jawab:
pembahasan:
v = 𝜔A cos 𝜔t
v = π.10 cos (π.¼)
v = 10π cos (180 . ¼)
v = 10π cos (45)
v = 10π . ½√2
v = 5π√2
9. Sebuah benda bermassa 0,15 kg bergerak harmonic sederhana pada sebuah ujung pegas yang memiliki konstanta pegas 200 N/m. kelajuan benda menjadi 0,2 m/s Ketika benda berada 1 cm dari posisi setimbangnya. Energi total benda ketika posisinya 5 mm dari posisi setimbangnya adalah…
A. 0,003 J
B. 0,013 J
C. 0,030 J
D. 0,053 J
E. 0,073 J
jawab: B
pembahasan:
Rumus energi toatal atau energi mekanik pegas elastisitas dan gerak harmonis sederhana:
EM = Ep + Ek
EM = ½ . k . y 2 + ½ . m . v 2
enegi mekanik saat y = 1 cm
EM = ½ . 200 . 0,01 2 + ½ . 0,15 . 0,2 2
EM = 0,01 + 0,003
EM = 0,013
kaena EM tetap maka saat posisi 5 mm EM juga benilai 0,013
selanjutnya berikut adalah 20 soal latihan gerak harmonik sederhana lengkap dengan pembahasannya:
Semogaa bermanfaat