pembahasan selanjutnya adalah
Soal tentang Jarak Titik ke Garis UN 2014
A. 4/3 √2 cm
B. 8/3 √2 cm
C. 4/3 √3 cm
D. 8/3 √3 cm
E. 8/3 √6 cm
Pembahasan
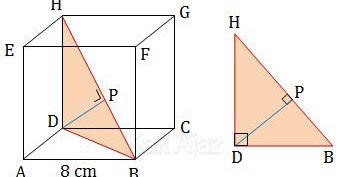
Perhatikan gambar ilustrasi untuk soal di atas!

Pandanglah segitiga BDH yang terdapat dalam kubus. Segitiga BDH adalah segitiga siku-siku di D.
DH adalah salah satu rusuk kubus.
DH = 8 cm
BD adalah diagonal bidang atau diagonal sisi.
BD = a√2
= 8√2 cm
Sedangkan HB adalah diagonal ruang kubus.
HB = a√3
= 8√3 cm
Jarak titik D ke garis HB adalah garis DP. Garis DP merupakan tinggi segitiga tersebut dengan alas HB. Sehingga dapat dirumuskan (rumus SMP):

Jika ketemu akar pecahan, gunakan rumus ini:

Sehingga diperoleh:
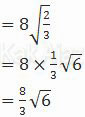
Jadi, jarak titik D ke garis HB adalah 8/3 √6 cm (E).
Soal tentang Jarak Titik ke Garis UN 2013
A. 3√6 cm
B. 6√6 cm
C. 9√6 cm
D. 3√10 cm
E. 9√10 cm

Pembahasan
Perhatikan gambar ilustrasi berikut ini!
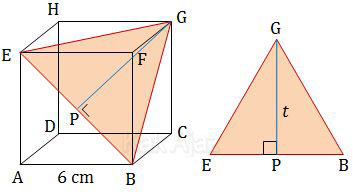
Pandanglah segitiga BEH yang terdapat dalam kubus. BE, EG, dan BG adalah diagonal bidang kubus.
BE = EG = BG = a√2
= 6√2
Dengan demikian, segitiga BEH adalah segitiga sama sisi dengan sisi s = 6√2.
Jarak titik G ke diagonal BE merupakan tinggi segitiga BEH. Tinggi segitiga sama sisi dirumuskan (sekali lagi rumus SMP):
t = ½ s √3
GP = ½ × 6√2 × √3
= 3√6
Jadi, jarak titik G ke diagonal BE adalah 3√6 cm (A).
Soal tentang Jarak Titik ke Garis UN 2011
A. 4√6 cm
B. 4√5 cm
C. 4√3 cm
D. 4√2 cm
E. 4 cm
Pembahasan
Berikut ini gambar ilustrasi dari soal di atas.
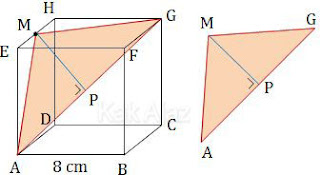
Perhatikan segitiga AGM! Segitiga tersebut sama kaki sehingga titik P terletak tepat di tengah AG.
Sekarang kita tentukan sisi-sisi segitiga AGM.
AG adalah diagonal ruang kubus.
AG = a√3
= 8√3 cm
AP adalah setengah AG.
AP = ½ AG
= ½ × 8√3 cm
= 4√3 cm
Panjang AM = GM. Garis AM merupakan sisi miring segitiga siku-siku AEM sehingga panjangnya dapat ditentukan dengan teorema Pythagoras.
AM = √(AE2 + EM2)
= √(82 + 42)
= 4√(22 + 12)
= 4√5
Nah, sekarang masuk ke pertanyaan. Jarak M ke AG adalah garis MP.
MP = √(AM2 − AP2 )
= √[(4√5)2 − (4√3)2]
= 4√[(√5)2 − (√3)2]
= 4√(5 − 3)
= 4√2
Jadi, jarak M ke AG adalah 4√2 cm (D).
Soal tentang Jarak Titik ke Garis UN 2015
A. √30 cm
B. 5√2 cm
C. 5√3 cm
D. 2√30 cm
E. 5√5 cm
Pembahasan
Soal di atas dapat diilustrasikan dengan gambar sebagai berikut:

Pandanglah segitiga MCE dalam kubus ABCD.EFGH.
CE adalah diagonal ruang kubus.
CE = a√3
= 10√3 cm
Panjang EM = CM. Garis CM adalah sisi miring segitiga siku-siku BCM sehingga dapat dicari dengan rumus Pythagoras.
CM = √(BC2 + BM2)
= √(102 + 52)
= 5√(22 + 12)
= 5√5
Sementara itu, QM merupakan garis tinggi segitiga MCE dengan alas CE. QM juga merupakan sisi segitiga siku-siku MQC sehingga juga dapat ditentukan rumus Pythagoras.
QM = √(CM2 − QC2 )
= √[(5√5)2 − (5√3)2]
= 5√[(√5)2 − (√3)2]
= 5√(5 − 3)
= 5√2
Jarak E ke CM adalah garis EP. Sedangkan EP merupakan garis tinggi segitiga MCE dengan alas CM. Dengan demikian, berlaku:
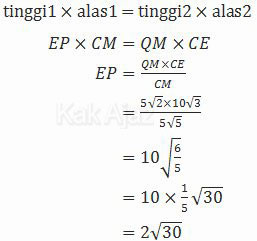
Jadi, Jika titik M tengah-tengah AB, jarak titik E ke CM adalah 2√30 cm (D).
Soal tentang Jarak Titik ke Bidang UN 2012
A. 1/3 √3 cm
B. 2/3 √3 cm
C. 4/3 √3 cm
D. 8/3 √3 cm
E. 16/3 √3 cm
Pembahasan
Perhatikan kubus ABCD.EFGH berikut ini!
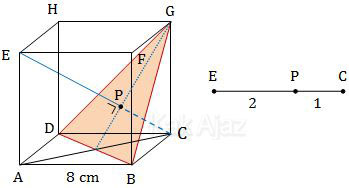
Titik E akan tegak lurus dengan bidang BDG apabila dihubungkan dengan titik C. EC merupakan diagonal ruang kubus.
EC = a√3
= 8√3 cm
Jarak titik E ke bidang BDG adalah garis EP. Sedangkan panjang EP adalah 2/3 diagonal ruang.
EP = 2/3 EC
= 2/3 × 8√3
=16/3 √3
Jadi, Jarak titik E ke bidang BGD adalah 16/3 √3 cm (E).
Pembahasan soal tentang Jarak Titik, Garis, dan Bidang yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 23
Pembahasan Matematika IPA UN 2014 No. 22
Pembahasan Matematika IPA UN 2015 No. 24
Pembahasan Matematika IPA UN 2016 No. 22
Pembahasan Matematika IPA UN 2017 No. 30
Pembahasan Matematika IPA UN 2017 No. 31
Pembahasan Matematika IPA UN 2018 No. 25
Pembahasan Matematika IPA UN 2019 No. 22 dan 23
Pembahasan Matematika IPA UN 2019 (2) No. 25
Pembahasan Matematika IPA UN 2019 (2) No. 26
Simak juga, Pembahasan Matematika IPA UN: Sudut antara Garis dan Bidang {Dimensi Tiga].
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat