pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 21 sampai dengan nomor 25 tentang:
- integral fungsi aljabar,
- dimensi tiga (jarak titik ke garis),
- dimensi tiga (jarak titik ke bidang),
- trigonometri, dan
- grafik fungsi trigonometri.
Soal No. 21 tentang Integral Fungsi Aljabar
A. x3 − 5/2 x2 + 4x + C
B. x3 − 5x2 + 4x + C
C. 3x3 − 5x2 + 4x + C
D. 6x3 − 5x2 + 4x + C
E. 6x3 − 5/2 x2 + 4x + C
Pembahasan
Ini termasuk soal penggembira, soal integral yang paling dasar. Tapi ingat, harus tetap cermat dan hati-hati. Ok, kita selesaikan sekarang.
∫(3x2 − 5x + 4) dx
= 3 ∙ 1/3 x3 − 5 ∙ 1/2 x2 + 4x + C
= x3 − 5/2 x2 + 4x + C
Jadi, hasil dari integral di atas adalah opsi (A).
Perdalam materi ini di Pembahasan Matematika UN: Integral Fungsi Aljabar.
Soal No. 22 tentang Dimensi Tiga (jarak titik ke garis)
A. 3/2 √6 cm
B. 3√2 cm
C. 3√6 cm
D. 6 cm
E. 9 cm

Pembahasan
Perhatikan gambar berikut ini!

Pandang segitiga PQR, mari kita tentukan panjang sisi-sisinya!

Jika diperhatikan sisi-sisi segitiga PQR, ternyata berlaku hukum Pythagoras.
QR2 = PQ2 + PR2
72 = 18 + 54
Sehingga segitiga PQR adalah segitiga siku-siku di titik P.

Jarak titik P ke garis QR merupakan tinggi segitiga siku-siku (PP’). Rumus tinggi segitiga siku-siku adalah perkalian sisi tegak dibagi sisi miring.

Jadi, jarak dari titik P ke garis QR adalah 3/2 √6 cm (A).
Perdalam materi ini di Pembahasan Matematika UN: Jarak Titik, Garis, dan Bidang.
Soal No. 23 tentang Dimensi Tiga (jarak titik ke bidang)
A. 10/3 √3 cm
B. 8/3 √3 cm
C. 7/3 √3 cm
D. 5/3 √3 cm
E. 4/3 √3 cm
Pembahasan
Perhatikan gambar di bawah ini!
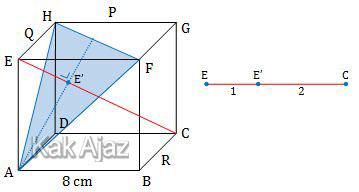
Titik E akan tegak lurus dengan bidang AFH apabila dihubungkan dengan titik C. Jarak EC merupakan diagonal ruang. Sedangkan jarak E ke bidang AFH adalah 1/3 diagonal ruang.
EE’ = 1/3 EC
= 1/3 ∙ 8√3
= 8/3 √3
Jadi, Jarak titik E ke bidang AFH adalah 8/3 √3 cm (B).
Perdalam materi ini di Pembahasan Matematika UN: Jarak Titik, Garis, dan Bidang.
Soal No. 24 tentang Trigonometri
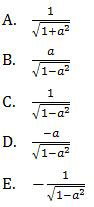
Pembahasan
Perhatikan gambar berikut ini!

Karena x sudut tumpul (kuadran II) maka cos x dan sec x bernilai negatif.

Jadi, nilai dari sec x adalah opsi (E).
Perdalam materi ini di Pembahasan Matematika UN: Perbandingan Trigonometri.
Soal No. 25 tentang Grafik Fungsi Trigonometri



Pembahasan
Kita tentukan pembuat nol-nya dulu.
y = 0
sin 2x = 0
2x = 0°, 180°, 360°, …
x = 0°, 90°, 180°, …
Grafik fungsi sinus dengan pembuat nol di atas adalah:

Jadi, grafik fungsi y=sin2x adalah grafik pada opsi (C).
Perdalam materi ini di Fungsi Trigonometri dan Grafknya [Soal UN dan Pembahasan]..
Simak Pembahasan Soal Matematika IPA UN 2019 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
