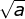Rangkuman Materi, Contoh Soal & Pembahasan Pangkat Dan Akar SD

Pangkat

Bilangan berpangkat secara umum dapat ditulis sebagai berikut:
aⁿ  , yang memiliki arti bahwa perkalian antarbilangan a sebanyak n kali.
aⁿ  = a x a x a x … x a → sebanyak n kali

Pangkat dua

Bilangan pangkat dua disebut juga dengan bilangan kuadrat. Secara umum ditulis a² .
a²  = a x a , dibaca a pangkat dua atau a kuadrat. Bilangan pangkat dua dapat dihitung dengan melakukan perkalian berulang dari bilangan tersebut.

Contoh:
4² = 4 x 4 , dibaca empat pangkat dua atau empat kuadrat

Perlu diingat!

1² = 1

2² = 4

3² = 9

4² = 16

5² = 25

6² = 36

7² = 49

8² = 64

9² = 81

10² = 100

Pangkat tiga

Bilangan pangkat tiga disebut juga dengan kubik. Secara umum ditulis a³ .
a³  = a x a x a  , dibaca a pangkat tiga atau a kubik.

Contoh:
8³ = 8 x 8 x 8 , dibaca delapan pangkat tiga atau delapan kubik.

Perlu diingat!

1 x 1 x 1 = 1³ = 1

2 x 2 x 2 = 2³ = 8

3 x 3 x 3 = 3³ = 27

4 x 4 x 4 = 4³ = 64

5 x 5 x 5 = 5³ = 125

6 x 6 x 6 = 6³ = 216

7 x 7 x 7 = 7³ = 343

8 x 8 x 8 = 8³ = 512

9 x 9 x 9 = 9³ = 729

10 x 10 x 10 = 10³ = 1000

Akar

Akar pangkat dua

Akar pangkat dua atau akar kuadrat dilambangkan dengan √, merupakan kebalikan dari pangkat dua. Bentuk umum akar pangkat dua dapat ditulis sebagai berikut:

= b atau a = b²

Contoh:

Perlu diingat!

1² = 1 x 1 = 1 maka akar pangkat dua dari 1 = 1

2² = 2 x 2 = 4 maka akar pangkat dua dari 4 = 2

3² = 3 x 3 = 9 maka akar pangkat dua dari 9 = 3

4² = 4 x 4 = 16 maka akar pangkat dua dari 16 = 4

5² = 5 x 5 = 25 maka akar pangkat dua dari 25 = 5

6² = 6 x 6 = 36 maka akar pangkat dua dari 36 = 6

7² = 7 x 7 = 49 maka akar pangkat dua dari 49 = 7

8² = 8 x 8 = 64 maka akar pangkat dua dari 64 = 8

9² = 9 x 9 = 81 maka akar pangkat dua dari 81 = 9

10² = 10 x 10 = 100 maka akar pangkat dua dari 100 = 10

Bilangan hasil perpangkatan pangkat dua adalah bilangan kuadrat sempurna, yaitu: 1,4,9,16,25,36,49,64,81,100,…

Atau

1² = 1  berarti = 1

2² = 4 berarti = 2

3² = 9 berarti = 3

4² = 16 berarti = 4

5² = 25 berarti = 5

6² = 36 berarti = 6

7² = 49 berarti = 7

8² = 64 berarti = 8

9² = 81 berarti = 9

10² = 100 berarti = 10

Akar pangkat tiga

Akar pangkat tiga dilambangkan dengan  , merupakan kebalikan dari pangkat tiga. Bentuk umum akar pangkat tiga dapat ditulis sebagai berikut:

= b atau a = b³

Contoh:

1³ = 1 x 1 x 1 = 1 maka akar pangkat tiga dari 1 = 1

2³ = 2 x 2 x 2 = 8 maka akar pangkat tiga dari 8 = 2

3³ = 3 x 3 x 3 = 27 maka akar pangkat tiga dari 27 = 3

4³ = 4 x 4 x 4 = 64 maka akar pangkat tiga dari 64 = 4

5³ = 5 x 5 x 5 = 125 maka akar pangkat tiga dari 125 = 5

6³ = 6 x 6 x 6 = 216 maka akar pangkat tiga dari 216 = 6

7³ = 7 x 7 x 7 = 343 maka akar pangkat tiga dari 343 = 7

8³ = 8 x 8 x 8 = 512 maka akar pangkat tiga dari 512 = 8

9³ = 9 x 9 x 9 = 729 maka akar pangkat tiga dari 729 = 9

10³ = 10 x 10 x 10 = 1000 maka akar pangkat tiga dari 1000 = 10

Bilangan hasil perpangkatan pangkat tiga disebut dengan bilangan kubik, yaitu:1,8,27,64,125,216,343,512,729,1000,…

Atau

1³ = 1  berarti  = 1

2³ = 8 berarti  = 2

3³ = 27 berarti  = 3

4³ = 64 berarti  = 4

5³ = 125 berarti  = 5

6³ = 216 berarti  = 6

7³ = 343 berarti  = 7

8³ = 512 berarti  = 8

9³ = 729 berarti  = 9

10³ = 1000 berarti  = 10

Soal No.1

42² = …

1. 42 x 2
2. 42 x 42
3. 42 x 2 x 45
4. 42 + 42

PEMBAHASAN :
Bilangan pangkat dua dapat dihitung dengan melakukan perkalian berulang dari bilangan tersebut.
42² = 42 x 42
Jawaban B

Soal No.2

Hasil perhitungan dari 5² – 3² + 2² = …

1. 20
2. 12
3. 24
4. 30

PEMBAHASAN :
5² – 3² + 2² = (5 x 5) – (3 x 3) + (2 x 2)
.                     = 25 – 9 + 4
.                     = 16 + 4
.                     = 20

Jawaban A

Soal No.3

Hasil perhitungan dari 15³ = …

1. 225
2. 375
3. 225
4. 1.125

PEMBAHASAN :
15³ = 15 x 15 x 15
.      = 225 x 15
.      = 3.375
Jawaban B

Soal No.4

Hasil perhitungan dari 20² – 12² = …

1. 32
2. 8
3. 544
4. 256

PEMBAHASAN :
20² – 12² = (20 x 20) – (12 x 12)
.                 = 400 – 144
.                 = 256
Jawaban D

Soal No.5

Hasil perhitungan dari 8² + 2³ = …

1. 10
2. 36
3. 72
4. 84

PEMBAHASAN :
8² + 2³ = (8 x 8) + (2 x 2 x 2)
.             = 64 + 8
.             = 72
Jawaban C

Soal No.6

Hasil perhitungan dari 56² – 48² = …

1. 104
2. 832
3. 583
4. 768

PEMBAHASAN :
56² – 48² = (56 x 56) – (48 x 48)
.                 = 3.136 – 2.304
.                 = 832
Jawaban B

Soal No.7

Hasil perhitungan dari 12³ : 8² = …

1. 32
2. 27
3. 42
4. 36

PEMBAHASAN :
12³ : 8² = (12 x 12 x 12) : (8 x 8)
.             = 1.728 : 64
.             = 27
Jawaban B

Soal No.8

Hasil perhitungan dari  = …

PEMBAHASAN :
Hitung setiap pilihan untuk mengetahui hasilnya, sebagai berikut:

1. 16 → 16³ = 16 x 16 x 16 = 4.096
2. 17 → 17³ = 17 x 17 x 17 = 4.913
3. 18 → 18³ = 18 x 18 x 18 = 5.832
4. 19 → 19³ = 19 x 19 x 19 = 6.859

Maka = 19
Jawaban D

Soal No.9

Hasil perhitungan dari  – 3² = …

PEMBAHASAN 
 – 3² = 17 – 9 = 8
Jawaban A

Soal No.10

Hasil perhitungan dari (42 – 32)² + 5³ = …

1. 125
2. 135
3. 175
4. 115

PEMBAHASAN :
(42 – 32)² + 5³ = 10² + 5³
.                = (10 x 10) + (5 x 5 x 5)
.                = 100 + 75
.                = 175
Jawaban C

Soal No.11

Hasil perhitungan dari (2 x 3)³ – (24 + 36) = …

1. 156
2. 144
3. 216
4. 269

PEMBAHASAN :
(2 x 3)³ – (24 + 36) = 6³ – 60
.                                   = 216 – 60
.                                   = 156
Jawaban A

Soal No.12

Hasil perhitungan dari 4³ + (27 : 9)² = …

1. 64
2. 56
3. 68
4. 73

PEMBAHASAN :
4³ + (27 : 9)² = (4 x 4 x 4) + 3²
.                        = (4 x 4 x 4) + (3 x 3)
.                        = 64 + 9
.                        = 73
Jawaban D

Soal No.13

Hasil perhitungan dari (7 – 2)² : (3 + 2) = …

1. 6
2. 3
3. 5
4. 7

PEMBAHASAN :
(7 – 2)² : (3 + 2) = 5² : 5 = 25 : 5 = 5
Jawaban C

Soal No.14

Hasil perhitungan dari 7² – (14 – 8)² = …

1. 12
2. 13
3. 14
4. 15

PEMBAHASAN :
7² – (14 – 8)² = (7 x 7) – 6²
.                = (7 x 7) – (6 x 6)
.                = 49 – 36
.                = 13
Jawaban B

Soal No.15

Hasil perhitungan dari  – 2³ = …

1. 4
2. 5
3. 6
4. 7

PEMBAHASAN :
 – 2³ = 14 – (2 x 2 x 2)
⇔ 14 – 8
⇔ 6
Jawaban C

Soal No.16

Hasil perhitungan dari 9² + 4² –  = …

1. 68
2. 72
3. 81
4. 78

PEMBAHASAN :
9² + 4² –  = (9 x 9) + (4 x 4) – 25
.                = 81 + 16 – 25
.                = 72
Jawaban B

Soal No.17

Luas suatu persegi adalah 225 cm² . Maka panjang sisinya adalah … cm.

1. 25
2. 35
3. 5
4. 15

PEMBAHASAN :
Luas persegi = 225 cm²
Rumus luas persegi = s x s = s²
225 = s²
s =
s = 15 cm
Jawaban D

Soal No.18

Bangun persegi memiliki panjang sisi 24 cm. Maka luas persegi tersebut adalah … cm² .

1. 196
2. 256
3. 436
4. 576

PEMBAHASAN :
Panjang sisi = s = 24 cm
Rumus luas persegi = s² = s x s
Maka luas persegi = 24 cm x 24 cm
.                                 = 576 cm²
Jawaban D

Soal No.19

Sebuah ember berbentuk kubus memiliki panjang sisi 20 cm. Ember tersebut akan penuh terisi air sebanyak … liter.

1. 8
2. 10
3. 12
4. 14

PEMBAHASAN :
Panjang sisi kubus = 20 cm
1 liter  = 1.000 cm³
Rumus volume kubus = s x s x s = s^{3</sup
Maka Volume kubus = 20 cm x 20 cm x 20 cm
.                                     = 8.000 cm3}
.                                     = 8.000 : 1000
.                                     = 8 liter
Jawaban A

Soal No.20

Sebuah bak mandi berbentuk kubus memiliki volume  sebesar 1.728 liter sehingga panjang sisi bak mandi tersebut adalah …

1. 12 dm
2. 14 dm
3. 16 dm
4. 18 dm

PEMBAHASAN :
Volume kubus = 1.728 liter
1 liter = 1 dm³
Rumus volume kubus = s x s x s = s³
Maka panjang sisi bak mandi dapat dihitung sebagai berikut:
Volume kubus = s³
1.728 = s³
s =
s = 12 dm
Jawaban A