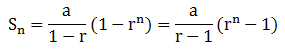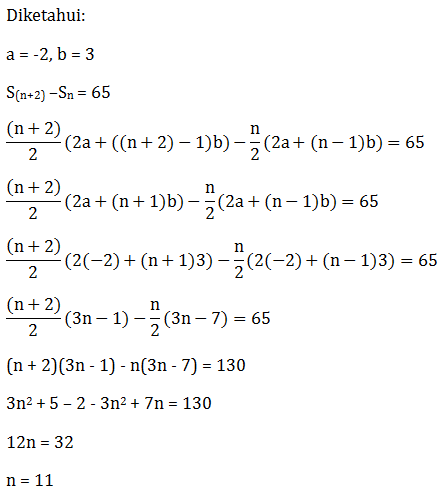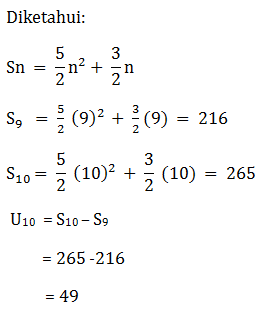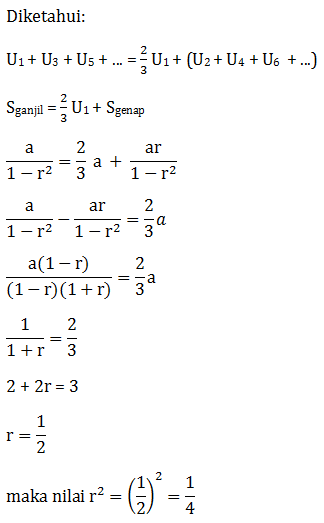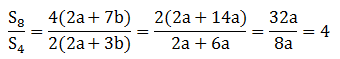Rangkuman, Contoh Soal & Pembahasan Barisan & Deret

Barisan dan Deret Aritmetika

1. Barisan Aritmetika
   Barisan aritmetika adalah suatu barisan dengan selisih (beda) antara dua suku yang berurutan selalu tetap. Berlaku:
   U_n – U_{n – 1} = b atau U_n = U_{n – 1} + b
   U_n = a + (n – 1)b
   Keterangan:
   U_n = suku ke-n
   a = suku pertama
   b = beda
   n = banyaknya suku
2. Deret Aritmetika
   Merupakan jumlah suku-suku dari barisan aritmetika. Rumus jumlah n suku pertama deret aritmatika adalah:
   Keterangan :
   S_n = jumlah suku ke-n
   U_n = suku ke-n
   a = suku pertama
   b = beda
   n = banyaknya suku

Barisan dan Deret Geometri

2. Barisan geometri
   Merupakan barisan bilangan dengan perbandingan setiap suku dengan suku sebelumnya selalu sama. Perbandingan setiap dua suku berurutannya disebut rasio (r). Bentuk umum suku ke–n barisan geometri yaitu sebagai berikut.
   U_n = ar^n-1
   Keterangan :
   Un =suku ke-n
   a = suku pertama
   r = rasio
   n = banyaknya suku
3. Deret Geometri
   Merupakan penjumlahan dari suku-suku suatu barisan geometri. Bentuk umum jumlah n suku pertama deret geometri dituliskan sebagai berikut.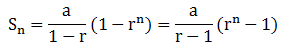
   
   Dengan :
   S_n = jumlah n suku pertama
   a = suku pertama
   r = rasio
   n = banyaknya suhu

Deret Tak Hingga

Terdiri dari dua jenis:

• Deret geometri konvergen (nilainya memusat) jika :
  -1 < r < 1 s dengan S­_∞ =
• Deret geometri konvergen (nilainya memusat) jika :
  r < -1 atau r > 1, maka S­_∞ = ± ∞

Versi 1

Versi 2

Soal No.3 (SBMPTN 2013)

Diketahui a, b, dan c berturut-turut adalah suku ke-2, ke-4, dan ke-6 barisan aritmatika. Jika maka nilai b adalah…

1. -2
2. -1
3. 1
4. 2
5. 4

PEMBAHASAN :

Jawaban : A

Soal No.4 (UN 2010)

Diketahui barisan aritmatika dengan U_n adalah suku ke-n. Jika U₂ + U₁₅ + U₄₀ = 165 maka U₁₉ =…

1. 10
2. 19
3. 28,5
4. 55
5. 82,5

PEMBAHASAN :
U_n = a + (n-1)b
U₂ + U₁₅ + U₄₀ = 165
(a+b) + (a+14b) + (a+39b) = 165
3a + 54b = 165
3(a+18b)= 165
a + 18b = 55
U₁₉ = 55
Jawaban : D

Soal No.5 (SNMPTN 2009)

Misalkan U_n menyatakan suku ke-n suatu barisan geometri. Jika diketahui U₅ = 12 dan log U₄ + log U₅ – log U₆ = log 3, maka nilai U₄ adalah …

1. 12
2. 10
3. 8
4. 6
5. 4

PEMBAHASAN :
Diketahui:
U₅ = 12
ar⁴ = 12 …..pers 1
log U₄+ log U₅ – log U₆ = log 3
log
ar² = 3… pers 2
Dari pers 1 dan 2 didapat:
r =2, a= 3/4
Sehingga U₄ = ar³ = 3/4(2)³ = 3/4.8 = 6
Jawaban : D

Soal No.6 (UN 2013)

Diketahui suku ke-3 dan suku ke-8 suatu barisan aritmetika berturut-turut adalah 2 dan -13. Jumlah 20 suku pertama deret tersebut adalah …

1. -580
2. -490
3. -440
4. -410
5. -380

PEMBAHASAN :
U_n = a + (n-1)b
Diketahui:
U₃ = a + 2b = 2
U₈ = a + 7b = -13
-5b = 15
b = -3, maka a = 8
S_n = n/2 (2a + (n-1)b)
S₂₀ = 20/2 (2(8) + 19(-3)) = 10 (16 – 57) = -410
Jawaban : E

Soal No.7 (SNMPTN 2012)

Jika suku pertama barisan aritmetika adalah -2 dengan beda 3, S_n adalah jumlah n suku pertama deret aritmetika tersebut, dan S_(n+2) – S_n = 65 maka nilai n adalah …

1. 11
2. 12
3. 13
4. 14
5. 15

PEMBAHASAN :

Jawaban : A

Soal No.8 (UN 2012)

Jumlah n suku pertama suatu deret aritmatika dinyatakan dengan S_n = n² + n. Suku ke-10 deret aritmetika tersebut adalah …

1. 49
2. 47
3. 35
4. 33
5. 28

PEMBAHASAN :

Jawaban : A

Soal No.9 (SBMPTN 2010)

Jumlah 50 suku pertama log 5 + log 55 + log 605 + log 6655 + … adalah …

1. log (55¹¹⁵⁰)
2. log (5²⁵ 11¹²²⁵)
3. log (25²⁵ 11¹²²⁵)
4. log (275¹¹²⁵)
5. 1150 log (5)

PEMBAHASAN :
Diketahui
Deret aritmetika dengan a = log 5, b = log 11
Menentukan jumlah 50 suku pertama (S₅₀)
S₅₀ = (2 log 5 + 49 log 11)
S₅₀ = 25 (2 log 5 + 49 log 11)
S₅₀ = 50 log 5 + 1225 log 11
S₅₀ = log 5⁵⁰ . 11¹²²⁵
S₅₀ = log 25²⁵ 11¹²²⁵
Jawaban : C

Soal No.10 (UN 2012)

Seorang penjual daging pada bulan Januari dapat menjual 120 kg, bulan Februari 130 kg, Maret dan seterusnya selama 10 bulan selalu bertambah 10 kg dari bulan sebelumnya. Jumlah daging yang terjual selama 10 bulan adalah…

PEMBAHASAN :
Diketahui:
a = 120
b = (130-120) = 10
Menentukan jumlah daging selama 10 bulan (S₁₀)
S₁₀ = (2(120)+9(10)) = 1650
Jawaban : D

Soal No.11 (SBMPTN 2013)

Diketahui deret geometri tak hingga U₁ + U₂ +U₃ + … Jika rasio deret tersebut adalah r dengan – 1 ₁ + U₃ + U₅ + … = U₁ + (U₂ + U₄ + U₆ + …) maka nilai r²=…

1. 
2. 
3. 
4. 
5. 1

PEMBAHASAN :

Jawaban : B

Soal No.12 (UN 2000)

Dari deret aritmetika diketahui suku tengah 32. Jika jumlah n suku pertama deret itu 672, banyak suku deret itu adalah..

1. 17
2. 19
3. 21
4. 23
5. 25

PEMBAHASAN :

Jawaban : C

Soal No.13 (SNMPTM 2012)

Jika a adalah suku pertama, r adalah rasio, dan Sn = 5⁽ⁿ⁺²⁾ – 25 adalah jumlah n suku pertama deret geometri maka nilai a + r =…..

1. 95
2. 105
3. 125
4. 225
5. 500

PEMBAHASAN :
Diketahui:
S_n = 5⁽ⁿ⁺²⁾ – 25
S_n = 52 . 5ⁿ – 5²
S_n = 25.5ⁿ – 25

Menentukan a dan r
Rumus S_n deret geometri

maka :
r = 5

a = 100
Sehingga, a + r = 100 + 5 = 105
Jawaban : B

Soal No.14 (UN 2007)

Suku ke-5 sebuah deret aritmetika adalah 11 dan jumlah nilai suku ke-8 dengan suku ke-12 sama dengan 52. Jumlah 8 suku pertama deret itu adalah…

1. 68
2. 72
3. 76
4. 80
5. 84

PEMBAHASAN :
Diketahui:
U₅ = a + 4b = 11 … pers 1
U_a + U₁₂ = 52
(a+7b)+(a+11b) = 52
2a + 18b = 52
a + 9b = 26 … pers 2

Menentukan jumlah 8 suku pertama (S₈)
Dari persamaan 1 dan 2
a + 9b = 26
a + 4b = 11 –
5b = 15
b = 3
maka a = -1
S₈ = 8/2 (2(-1)+7.3)
S₈ = 4 (-2+21)
S₈ = 76
Jawaban : C

Soal No.15 (SBMPTN 2014)

Jika suku pertama, ke-3 dan ke-6 suatu barisan aritmetika masing-masing adalah b-a, a, 36 serta jumlah 9 suku pertama barisan tersebut adalah 180, maka beda barisan tersebut adalah …

1. 18
2. 16
3. 12
4. 9
5. 6

PEMBAHASAN :

Jawaban : B

Soal No.16 (UN 1995)

Diketahui deret bilangan 10 + 11 + 12 + 13 + … + 99. Dari deret bilangan itu, jumlah bilangan yang habis dibagi 2 tetapi tidak habis dibagi 5 adalah…

1. 950
2. 1480
3. 1930
4. 1980
5. 2430

PEMBAHASAN :

Jawaban : D

Soal No.17 (SBMPTN 2014)

Diketahui a, a + b, dan 4a+b merupakan 3 suku berurutan suatu barisan aritmetika. Jika a, a+b, 4a+b+9 merupakan suatu barisan geometri maka a+b =…

1. 2
2. 3
3. 4
4. 5
5. 6

PEMBAHASAN :

• a, a+b, 4a+b (barisan aritmatika)
  U₁, U₂, U₃
  2U₂ = U₁ + U₃
  2(a+b) = a + 4a + b
  2a+2b = 5a+b
  b = 3a…pers 1

• a, a+b, 4a+b+9 (barisan geometri)
  U₁, U₂, U₃
  U₂² = U₁ . U₃
  (a+b)² = a(4a+b+9)
  (a+3a)² = a(4a+3a+9)
  16a² = 7a²+9a
  9a² – 9a = 0
  9a(a – 1) = 0
  a = 0 ∨ a=1

Jika a = 1 maka b = 3(1) = 3
maka a+b = 1+3 = 4
Jawaban : C

Soal No.18 (UN 2012)

Suku ke-3 dan suku ke-7 suatu deret geometri berturut-turut adalah 16 dan 256. Jumlah suku 7 suku pertama deret tersebut adalah …

1. 500
2. 504
3. 508
4. 512
5. 516

PEMBAHASAN :

Jawaban : C

Soal No.19 (UM UGM 2013)

Jumlah n suku pertama suatu deret aritmetika dinotasikan dengan S_n. Jika suku pertama deret tersebut tak nol dan S_4,S_8, S₁₆ membentuk barisan geometri maka = …

1. 2
2. 4
3. 6
4. 8
5. 10

PEMBAHASAN :
S_n termasuk deret aritmatika
S₄,S₈,S₁₆ termasuk barisan geometri

Menentukan beda (b)
S₄ = 2(2a+3b)
S₈ = 4(2a+7b)
S₁₆ = 8(2a+15b)
S₈² = S₄ S₁₆
16(2a+7b)² = 16(2a + 3b)(2a + 15b)
4a² + 28ab + 49b² = 4a² + 36ab + 45b²
4b² = 8ab
4b = 8a
b = 2a

Menentukan

Jawaban : B

Soal No.20 (UN 1993)

Suku pertama dan rasio barisan geometri berturut-turut 2 dan 3. Jika jumlah n suku pertama deret tersebut adalah 80, banyak suku barisan tersebut adalah

PEMBAHASAN :

Jawaban : B

Soal No.21 (SBMPTN 2014)

Diketahui a, a+b, a+5b merupakan 3 suku pertama suatu barisan geometri. Jika a, a+b, x, y dan z merupakan 5 suku pertama barisan aritmetika dan x + y + x = -15, maka suku ke 10 barisan aritmetika tersebut adalah…

1. 
2. -14
3. 
4. -15
5. 

PEMBAHASAN :

Jawaban : B

Soal No.22 (UN 2014)

Jumlah konsumsi gula pasir oleh penduduk suatu kelurahan pada tahun 2013 sebesar 1.000 kg dan selalu meningkat dua kali lipat setiap tahun. Total konsumsi gula penduduk tersebut tersebut pada tahun 2013 sampai dengan tahun 2018 adalah …

1. 62.000 kg
2. 63.000 kg
3. 64.000 kg
4. 65.000 kg
5. 66.000 kg

PEMBAHASAN :

Jawaban : B

Soal No.23 (SBMPTN 2014)

Jika S = 1 + sin2x + sin²2x + sin³ 2x+…

1. < S < 2
2. < S < 2
3. < S <
4. < S <
5. < S <

PEMBAHASAN :

Jawaban : A

Soal No.24 (UN 2014)

Seutas tali dipotong menjadi 5 bagian sehingga panjang potongan-potongan tali tersebut membentuk barisan geometri. Jika panjang potongan tali terpendek 6 cm dan tali terpanjang 96 cm maka panjang tali semula adalah ..

1. 96 cm
2. 185 cm
3. 186 cm
4. 191 cm
5. 192 cm

PEMBAHASAN :
Diketahui:
n = 5
a = 6
Menentukan rasio (r)
U₅ = ar⁴
96 = 6r⁴
r⁴ = 16
r = 2

Menentukan panjang tali semula

Jawaban : C

Soal No.25 (UN 2010)

Tiga buah bilangan membentuk barisan aritmatika dengan beda tiga. Jika suku kedua dikurangi 1,maka terbentuklah barisan geometri dengan jumlah 14. Rasio barisan tersebut adalah …

1. 4
2. 2
3. 
4. 
5. -2

PEMBAHASAN :
Misal tiga buah bilangan tersebut adalah:
x – 3, x, x + 3
Diketahui jumlah barisan geometri = 14, jika suku kedua dikurangi 1, Maka:
(x – 3) + (x – 1) + (x + 3) = 14
x = 5
deret aritmatika : 2, 4, 8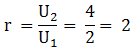

Jawaban : B

Soal No.26 (UN 2007)

Bakteri jenis A berkembang biak menjadi dua kali lipat setiap lima menit. Pada waktu lima belas menit pertama banyaknya bakteri ada 400. Banyak bakteri pada waktu tiga puluh menit pertama adalah …

1. 640 bakteri
2. 3.200 bakteri
3. 6.400 bakteri
4. 12.800 bakteri
5. 32.000 bakteri

PEMBAHASAN :
Diketahui U₃ = 400 (lima belas menit pertama)
Menentukan jumlah bakteri awal (a)
U₃ = 400
ar³ = 400
a.2³ = 400
a = 50
Menentukan jumlah bakteri tiga puluh menit pertama (U₇)
U₇ = ar⁷= 50(2)⁶ = 64.000 bakteri
Jawaban : C

Soal No.27 (UN 2009)

Sebuah ayunan mencapai lintasan pertama sejauh 90 cm dan lintasan berikutnya hanya mencapai dari lintasan sebelumnya. Panjang lintasan seluruhnya hingga ayunan berhenti adalah….

1. 120 cm
2. 144 cm
3. 240 cm
4. 250 cm
5. 260 cm

PEMBAHASAN :

Jawaban : C

Soal No.28 (UN 2013)

Sebuah bola tenis di jatuhkan dari ketinggian 2 m dan memantul menjadi tinggi sebelumnya. Panjang lintasan bola tenis tersebut sampai berhenti adalah…

1. 8 m
2. 16 m
3. 18 m
4. 24 m
5. 32 m

PEMBAHASAN :

Jawaban : C