pembahasan selanjutnya adalah
- bentuk akar,
- bilangan berpangkat,
- menyederhanakan bentuk akar,
- pola bilangan, dan
- barisan geometri.
Soal No. 6 tentang Bentuk Akar
A. √6
B. 5√6
C. 9√6
D. 10√6
Pembahasan
Perhatikan opsi jawabannya, semua mengandung √6. Artinya, angka dalam akar pada soal di atas harus dipecah menjadi 6x. Sehingga diperoleh:
√54 − √24 = √(6×9) − √(6×4)
= 3√6 − 2√6
= √6
Jadi, Hasil dari √54 − √24 adalah √6 (A).
Perdalam materi ini di Operasi Bilangan Bentuk Akar [Soal UN dan Pembahasan].
Soal No. 7 tentang Bilangan Berpangkat
A. 1/9
B. 1/3
C. 3
D. 9

Pembahasan
Langkah pertama, pangkatnya kita kalikan terlebih dahulu.
(271/2)2/3 = 271/3
Selanjutnya, bilangan pokok 27 kita ubah menjadi bentuk pangkat, yaitu 33. Setelah itu pangkatnya kita kalikan.
= (33)1/3
= 31
= 3
Jadi, hasil dari (271/2)2/3 adalah 3 (C).
Perdalam materi ini di Operasi Bilangan Berpangkat [Soal UN dan Pembahasan].
Soal No. 8 Menyederhanakan Bentuk Akar
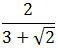
adalah ….
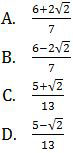
Pembahasan
Untuk menyelesaikan pecahan bentuk akar, cara yang paling umum adalah dengan mengalikan bilangan sekawan dari penyebutnya.
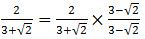
Perhatikan bentuk penyebutnya, bentuk tersebut dapat diselesaikan dengan rumus aljabar:
(a + b)(a − b) = a2 − b2
(3 + √2)(3 − √2) = 32 − (√2)2
Sehingga diperoleh:

Jadi, bilangan yang senilai dengan bentuk akar tersebut adalah opsi (B).
Soal No. 9 tentang Pola Bilangan
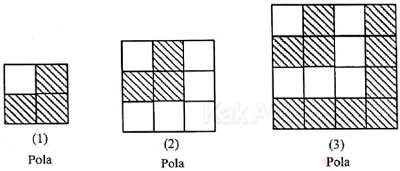
Selisih antara banyak persegi yang diarsir dengan yang tidak diarsir pada pola ke delapan adalah ….
A. 6
B. 7
C. 8
D. 9
Pembahasan
Yang dimaksud selisih pada soal di atas adalah selisih positif sehingga:
Pola 1 : |3 − 1| = 2
Pola 2 : |3 − 6| = 3
Pola 3 : |10 − 6| = 4
Perhatikan hasilnya: 2, 3, 4 adalah bilangan urut yang dimulai dari 2. Bisa diramalkan pola berikutnya adalah 5, 6, 7, dan seterusnya. Pola tersebut dapat dirumuskan:
Pola n = n + 1
Pola 8 = 8 + 1
= 9
Jadi, pola ke delapan pada pola tersebut adalah 9 (D).
Soal No. 10 tentang Barisan Geometri
A. 1.535
B. 1,536
C. 3.071
D. 3,072
Pembahasan
Diketahui:
U2 = 6
U4 = 24
Rasio barisan geometri tersebut adalah:
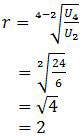
Suku ke-n barisan geometri dirumuskan:
Un = Uk rn−k
U10 = U4r10−4
= 24 × 26
= 24 × 64
= 1536
Jadi, suku ke sepuluh barisan geometri tersebut adalah 1.536 (B).
Simak Pembahasan Soal Matematika SMP UN 2016 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
