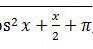Pembahasan Matematika No. 11 – 15 TKD Saintek SBMPTN 2015 Kode Naskah 502

• aplikasi turunan, 
• integral, 
• permutasi dan kombinasi, 
• peluang kejadian, serta 
• deret geometri tak hingga.

Soal No. 11 tentang Aplikasi Turunan

Fungsi

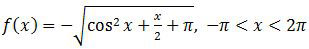
turun pada interval ….

A.   0 < x < 5π/12
B.   0 < x < π/12
C.   π/6 < x < π/3
D.   5π/12 < x < 7π/12
E.   −7π/12 < x < π/12 

Pembahasan

Untuk mempermudah menurunkan fungsi f(x), bentuk akar dalam fungsi tersebut kita ubah terlebih dahulu menjadi bentuk pangkat. Diperoleh: 

f(x) = −(cos²x + ½x + π)^½
 
Suatu fungsi akan turun jika turunan fungsi tersebut kurang dari nol. 

f’(x) < 0
−½(cos²x + ½x + π)^−½ (2cos x (−sin x) + ½) < 0
−½(cos²x + ½x + π)^−½ (−2sin x cos x + ½) < 0
−½(cos²x + ½x + π)^−½ (−sin 2x + ½) < 0
½(cos²x + ½x + π)^−½ (sin 2x − ½) < 0

Bentuk tersebut dapat dikembalikan ke bentuk akar sebagai berikut:

Perhatikan penyebutnya! Penyebut pecahan tersebut berbentuk akar. Bentuk akar selalu menghasilkan nilai positif atau definit positif sehingga dapat diabaikan. Dengan demikian, pertidaksamaan tersebut menjadi lebih sederhana.

sin 2x − ½ < 0
sin 2x < ½

Pembuat nol dari pertidaksamaan tersebut adalah:

sin 2x = ½

  x = 15° + k.180°
     = …, −165°, 15°, 195°, …
     = …, −11π/12, π/12, 13π/12, …

• 2x = (180° − 30°) + k.360°

     = 150° + k.360°
  x = 75° + k.180°
     = …, −105°, 75°, 255°, …
     = …, −7π/12, 5π/12, 17π/12, …

Berdasarkan opsi jawaban yang tersedia, opsi A dan B salah karena dalam penghitungan tidak diperoleh sudut 0. Opsi C salah karena tidak diperoleh sudut π/6 maupun π/3. Opsi D salah karena tidak diperoleh sudut 7π/12. Sehingga jawabannya adalah opsi E.

Jadi, fungsi f(x) turun pada interval −7π/12 < x < π/12 (E).

Soal No. 12 tentang Integral

Pada interval 0 ≤ x ≤ c, luas daerah di bawah kurva y = −x² dan di atas garis y = −3x sama dengan luas daerah di atas y = −x² dan di bawah y = −3x.

Nilai c = ….

A.   4½
B.   4¾
C.   5
D.   5⅕
E.   5⅓

Pembahasan

Kita tentukan dulu titik potong antara kurva dan garis. Titik potong ini akan kita gunakan sebagai batas integrasi.

         y₁ = y₂
       −x² = −3x
          x² = 3x
 x² − 3x = 0 
x(x − 3) = 0 
x = 0 dan x = 3

Dengan demikian, kurva dan garis tersebut berpotongan di x = 0 dan x = 3. Perhatikan gambar berikut ini!

L₁ menyatakan luas daerah di bawah kurva dan di atas garis sedangkan L₂ menyatakan luas daerah di atas kurva dan di bawah garis. Disebutkan pada soal bahwa L₁ = L₂ sehingga:

                          L₁ = L_{2
         0}∫³ (y₁ − y₂) dx = ₃∫^c (y₂ − y₁) dx 
     ₀∫³ (−x² + 3x) dx = ₃∫^c (−3x + x²) dx
−1/3 x³ + 3/2 x² ]³ = −3/2 x² + 1/3 x³ ]₃^c
  −1/3 . 27 + 3/2 . 9 = −3/2 c² + 1/3 c³ − (−3/2 . 9 + 1/3 . 27)
                          9/2 = −3/2 c² + 1/3 c³ + 9/2
                      3/2 c² = 1/3 c³
                          3/2 = 1/3 c
                             c = 3/2 × 3
                                = 9/2

Jadi, nilai c adalah 4½ (A)

Soal No. 13 tentang Permutasi dan Kombinasi

Pembahasan

Kurva Ax² − (By/2)² = 0 tidak akan terjadi apabila nilai A atau B sama dengan 0 sehingga tinggal 4 pilihan yang harus diambil untuk nilai A dan B. Karena A dan B adalah dua bilangan yang berbeda serta AB ≠ BA maka soal di atas harus diselesaikan dengan permutasi (4 permutasi 2). 

₄P₂ = 4!/(4 − 2)!
       = 4!/2!
       = 4 × 3
       = 12

Jadi, banyaknya kurva yang terjadi adalah 12 (E).

Catatan:

Karena nilai B pada kurva di atas dikuadratkan, maka untuk B = 1 dan B = −1 akan menghasilkan harga yang sama. Sehingga untuk A dan B: (3, 1) dan (3, −1) akan menghasilkan kurva yang sama. Demikian juga untuk A dan B: (6, 1) dan (6, −1).

Dengan demikian, banyaknya kurva seharusnya:

12 − 2 = 10

Soal No. 14 tentang Peluang Kejadian

Pembahasan

Kita misalkan terlebih dahulu: 

S₁ : siswa kelas pertama 
S₂ : siswa kelas kedua 
P₁ : siswa perempuan kelas pertama 
P₂ : siswa perempuan kelas kedua 
L₁ : siswa laki-laki kelas pertama 
L₂ : siswa laki-laki kelas kedua

Dua kelas masing-masing terdiri atas 30 siswa. 

n(S₁) = 30 
n(S₂) = 30

Peluang terpilih keduanya perempuan adalah 23/180. 

P(P₁) . P(P₂) = 23/180

 
n(P₁) . n(P₂) = 115

Faktor dari 115 yang kurang dari 30 (karena jumlah siswa 30) adalah 5 dan 23. Dapat dikatakan bahwa n(P₁) = 5 dan n(P₂) = 23 atau sebaliknya, sehingga: 

n(L₁) = n(S₁) − n(P₁)
          = 30 − 5
          = 25 

n(L₂) = n(S₂) − n(P₂)
          = 30 − 23
          = 7

Dengan demikian, peluang terpilih keduanya laki-laki adalah:

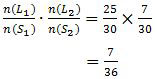
Jadi, peluang terpilih keduanya laki-laki adalah 7/36 (C).

Soal No. 15 tentang Deret Geometri Tak Hingga

Pembahasan

Nilai maksimum atau minimum suatu fungsi terjadi saat turunan fungsi tersebut sama dengan nol. 

     f(x) = −⅓ x³ + x + c
     f’(x) = 0
−x² + 1 = 0
         x² = 1
           x = ±1

Karena terdapat dua nilai x, yaitu x = 1 dan x = −1 maka fungsi f(x) mempunyai nilai maksimum dan minimum. Untuk mengetahui mana yang maksimum dan minimum kita uji dengan turunan kedua. 

f”(x) = −2x
f”(1) = −2×1 = −2      (maksimum) 
f”(−1) = −2×(−1) = 2  (minimum)
 
Dengan demikian, f(x) mencapai maksimum saat x = 1. Nilai maksimumnya adalah: 

f(1) = −⅓ 1³ + 1 + c
       = ⅔ + c

Nilai maksimum ini sama dengan jumlah suatu deret geometri tak hingga. 

S_∞ = ⅔ + c

Selisih suku kedua dan suku pertama deret geometri tersebut adalah −2f’(0). 

U₂ − U₁ = −2f’(0)    (f’(x) = −x² + 1)
   ar − a = −2(−0² + 1) 
a(r − 1) = −2

Sedangkan rasio deret geometri tersebut adalah r = 1 − 1/√2 sehingga: 

a(1 − 1/√2 − 1) = −2
             −1/√2 a = −2
                        a = 2√2

Sekarang kita gunakan rumus jumlah deret geometri tak hingga untuk mendapatkan nilai c.

          c = 4 − 2/3
             = 12/3 − 2/3
             = 10/3

Jadi, nilai c pada fungsi f(x) tersebut adalah 10/3 (A).

Simak Pembahasan Soal TKD Saintek SBMPTN 2015 selengkapnya.

Simak juga:
Pembahasan Matematika SBMPTN 2014
Pembahasan Matematika SBMPTN 2016
Pembahasan Matematika SBMPTN 2017
Pembahasan Matematika SBMPTN 2018
Pembahasan Matematika UTBK SBMPTN 2019

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih