Pembahasan Matematika IPS UN 2019 No. 31

Pembahasan soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPS nomor 31 sampai dengan nomor 36 tentang:

• median data, 
• varians data, 
• kaidah pencacahan [permutasi], 
• kaidah pencacahan [kombinasi], 
• teori peluang, dan 
• frekuensi harapan.

Soal No. 31 tentang Median Data

Histogram berikut menyatakan data nilai tes peserta didik kelas XI.

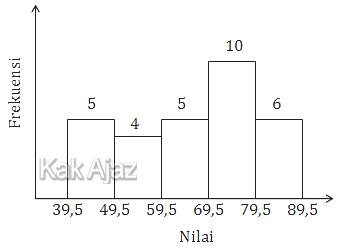
Median dari data tersebut adalah ….

A.   70,5
B.   71,2
C.   71,5
D.   75,5
E.   79,5

Pembahasan

Jumlah data di atas ada 30, berarti median terletak pada data ke-15.

   N = 5 + 4 + 5 + 10 + 6
       = 30
½ N = 15

Perhatikan cara menentukan besaran median!

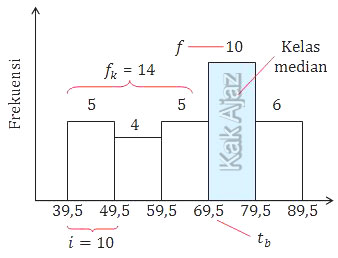
Median dapat ditentukan dengan rumus sebagai berikut:

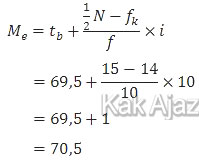
Jadi, median dari data tersebut adalah70,5 (A).

Soal No. 32 tentang Varians Data

Pembahasan

Rata-rata data tersebut adalah:

Varians adalah kuadrat dari simpangan baku sehingga perumusannya adalah:

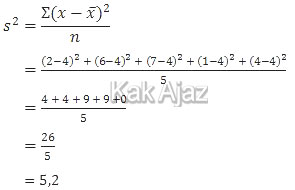
Jadi, varians data tersebut adalah 5,2 (-).

Soal No. 33 tentang Kaidah Pencacahan [permutasi]

Pembahasan

Ada dua kemungkinan memilih ketua, yaitu ketua dari kelas XI atau ketua dari kelas XII.

◇ Ketua dari kelas XI (4 siswa dipilih 1) sedangkan wakil dan sekretaris dari kelas X (3 siswa dipilih 2).

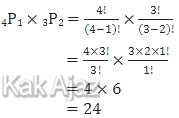
◇ Ketua dari kelas XII (5 siswa dipilih 1) sedangkan wakil dan sekretaris dari kelas XI dan X (7 siswa dari kelas X dan XI dipilih 2).

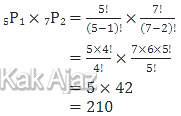
Total banyak cara adalah:

24 + 210 = 234

Jadi, banyak cara untuk memilih pengurus OSIS adalah 234 cara (D).

Soal No. 34 tentang Kaidah Pencacahan [kombinasi]

Pembahasan

Sebenarnya tinggal mengalikan saja, 4 × 3 = 12. Cuma karena Kak Ajaz terlanjur memberi judul ‘kombinasi’ maka Kak Ajaz bahas lebih lanjut.

4 putri dan 3 putra tersebut mempunyai kedudukan yang setara, tidak ada peringkat, sehingga bisa diselesaikan dengan rumus kombinasi. Dari 4 putri dipilih 1 dan dari 3 putra dipilih 1 maka banyak cara adalah:

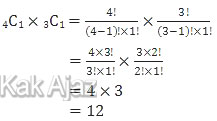
Jadi, banyak cara memilih pasangan ada sebanyak 12 cara (B).

Soal No. 35 tentang Teori Peluang

Pembahasan

Banyak semua kejadian terambilnya 6 bola dari 11 bola (kuning dan hijau) adalah:

Misal kejadian A adalah terambilnya 4 bola kuning dan 2 bola hijau, maka:

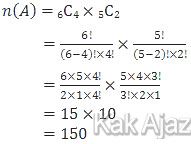
Peluang kejadian A adalah:

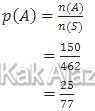
Jadi, peluang terambilnya 4 bola kuning dan 2 bola hijau adalah 25/77 (B).

Soal No. 36 tentang Frekuensi Harapan

Pembahasan

Banyak semua kejadian dua dadu dilempar bersama adalah:

n(S) = 6²
        = 36

Misal A adalah kejadian muncul mata dadu berjumlah 5 atau 10, maka:

A : (1, 4), (2, 3), (3, 2), (4, 1)
      (4, 6), (5, 5), (6, 4)

n(A) = 7

Peluang kejadian A adalah:

p(A) = n(A)/n(S)
        = 7/36

Frekuensi harapan kejadian A:

f_h(A) = p(A) × N
         = 7/36 × 180
         = 35

Jadi, frekuensi harapan muncul mata dadu berjumlah 5 atau 10 adalah 35 kali (E).

Simak Pembahasan Soal Matematika IPS UN 2019 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih