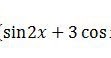pembahasan selanjutnya adalah
Integral Fungsi Trigonometri UN 2012
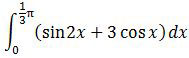
adalah ….
A. 3/4 + 2√3
B. 3/4 + 3√3
C. 1/4 (1 + 2√3)
D. 2/4 (1 + 2√3)
E. 3/4 (1 + 2√3)
Pembahasan
Berikut ini rumus dasar untuk menyelesaikan soal di atas.
∫ sin x dx = −cos x + C
∫ cos x dx = sin x + C
∫ sin ax dx = −1/a cos ax + C
∫ cos ax dx = 1/a sin ax + C
Dengan berpedoman pada rumus dasar di atas, diperoleh:
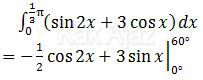
Kita ubah 1/3 π menjadi 60° agar lebih ramah di otak kita.
Ok, sekarang kita masukkan batas-batasnya.
= (−1/2 cos 120° + 3 sin 60°) − (−1/2 cos 0° + 3 sin 0°)
= [−1/2 (−1/2) + 3 ∙ 1/2 √3] − (−1/2 ∙ 1 + 3 ∙ 0)
= 1/4 + 3/2 √3 + 1/2
= 3/4 + 3/2 √3
= 3/4 + 6/4 √3
= 3/4 (1 + 2√3)
Jadi, hasil dari integral fungsi trigonometri di atas adalah opsi (E).
Integral Fungsi Trigonometri UN 2015
A. −1/2 cos 4x − cos 2x + C
B. −1/2 cos 4x + cos 2x + C
C. −1/4 cos 4x + 1/2 cos 2x + C
D. 1/4 cos 4x − 1/2 cos 2x + C
E. 1/4 cos 4x + 1/2 cos 2x + C

Pembahasan
Untuk menyelesaikan integral di atas, kita wajib mengingat kembali rumus jumlah dan selisih sinus dan kosinus berikut ini.
2 cos A sin B = sin (A + B) – sin (A – B)
Berdasarkan rumus di atas, diperoleh:
∫ 2 cos 3x sin x dx
= ∫ [sin (3x + x) – sin (3x – x)] dx
= ∫ (sin 4x – sin 2x) dx
Selanjutnya kita gunakan rumus pada pembahasan sebelumnya untuk menyelesaikan integral tersebut.
= –1/4 cos 4x + 1/2 cos 2x + C
Jadi, hasil dari integral di atas adalah opsi (C).
Integral Fungsi Trigonometri UN 2011
A. –1/10 sin52x + C
B. –1/10 cos52x + C
C. –1/5 cos52x + C
D. 1/5 cos52x + C
E. 1/10 sin52x + C
Pembahasan
Integral di atas adalah integral substitusi. Cirinya, terdiri dari dua fungsi yang bila salah satu fungsi diturunkan akan membagi habis fungsi yang lain.
Langkah pertama, mengganti dx dengan d(cos 2x), kemudian dibagi dengan turunan cos 2x. Dipilih d(cos 2x) karena cos 2x berpangkat lebih tinggi.
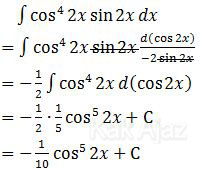
Jadi, hasil dari integral substitusi fungsi trigonometri tersebut adalah opsi (B).
Integral Fungsi Trigonometri UN 2014
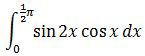
adalah ….
A. –4/3
B. –2/3
C. 1/3
D. 2/3
E. 4/3
Pembahasan
Langkah pertama adalah mengubah bentuk sin 2x.
sin 2x = 2 sin x cos x
Sehingga diperoleh:
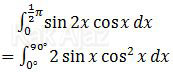
Bentuk terakhir ini adalah bentuk integral substitusi.
Mari kita kerjakan seperti soal sebelumnya.
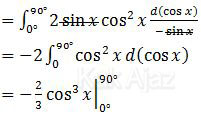
Sekarang tinggal memasukkan batas-batasnya.
= –2/3 cos3 90° – (–2/3 cos3 0°)
= 0 – (–2/3 ∙ 13 )
= 2/3
Jadi, hasil dari integral tersebut adalah 2/3 (D).
Integral Fungsi Trigonometri UN 2013
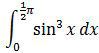
adalah ….
A. –1/3
B. –1/2
C. 0
D. 1/3
E. 2/3
Pembahasan
Rumus integral sin3 x memang ada. Tetapi, hanya menambah beban memori jika semua rumus integral kita hafalkan. Sekadar tahu saja, ada lebih dari 400 rumus integral.
Lebih baik sin3 x kita jabarkan sebagai berikut:
sin3 x = sin x sin2 x
= sin x (1 – cos2 x )
= sin x – sin x cos2 x
Dengan demikian, integral di atas menjadi:

Coba perhatikan, integral di atas terdiri dari dua suku. Suku pertama langsung bisa kita integralkan sedangkan suku yang kedua harus diintegralkan dengan substitusi.
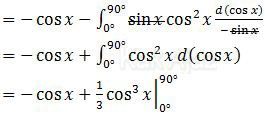
Ok, proses pengintegralan sudah selesai. Sekarang kita masukkan batas-batasnya.
= (–cos 90° + 1/3 cos3 x 90°) – (–cos 0° + 1/3 cos3 x 0°)
= 0 – (–1 + 1/3 ∙ 13)
= 1 – 1/3
= 2/3
Jadi, hasil dari integral tersebut adalah 2/3 (E).
Pembahasan soal Integral Fungsi Trigonometri yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 32
Pembahasan Matematika IPA UN 2014 No. 32 dan 33
Pembahasan Matematika IPA UN 2015 No. 34 dan 35
Pembahasan Matematika IPA UN 2016 No. 33
Simak juga, Pembahasan Matematika IPA UN: Luas Daerah [Aplikasi Integral].
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat