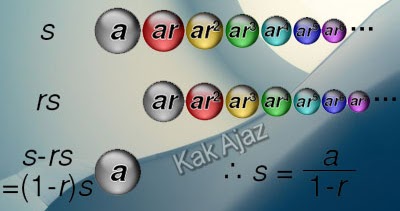
pembahasan selanjutnya adalah

Pembahasan soal-soal Ujian Nasional (UN) tahun 2019 bidang studi Matematika SMA-IPA nomor 11 sampai dengan nomor 15 tentang:
- barisan dan deret aritmetika,
- barisan dan deret geometri,
- deret geometri tak hingga,
- limit fungsi, dan
- limit fungsi mendekati tak hingga.
Soal No. 11 tentang Barisan dan Deret Aritmetika
| Minggu ke- | Lama Jogging (dalam menit) |
| 1 | 10 |
| 2 | 15 |
| 3 | 20 |
| … | … |
Jika lama jogging setiap minggunya mengalami peningkatan dengan jumlah yang tetap, total lama jogging yang dilakukan selama 8 minggu adalah ….
A. 210 menit
B. 220 menit
C. 255 menit
D. 315 menit
E. 440 menit
Pembahasan
Peningkatan lama waktu jogging pada soal d atas membentuk deret aritmetika dengan:
a = 10 menit
b = 5 menit
Total lama jogging selama 8 minggu memenuhi rumus:
Sn = ½ n [2a + (n − 1)b]
S8 = ½ × 8 [2 × 10 + (8 − 1)5]
= 4 (20 + 35)
= 220
Jadi, total lama jogging yang dilakukan selama 8 minggu adalah 220 menit (B).
Catatan: mestinya harus dikalikan 7 hari karena jogging dilakukan setiap hari.
Perdalam materi ini di Pembahasan Matematika UN: Barisan dan Deret.
Soal No. 12 tentang Barisan dan Deret Geometri
A. 48 bakteri
B. 64 bakteri
C. 96 bakteri
D. 128 bakteri
E. 192 bakteri

Pembahasan
Ini adalah soal deret geometri dengan:
a = 2
r = 2
Yang perlu diperhatikan adalah pernyataan: setiap 2 hari, 1/4 dari jumlah bakteri mati.
Agak repot juga jika kita kerjakan dengan rumus deret geometri. Lebih baik kita kerjakan secara manual seperti tabel berikut ini.
| Hari | Jumlah Bakteri | Mati | Hidup |
| awal | 2 | 2 | |
| 1/2 hari | 4 | 4 | |
| 1 hari | 8 | 8 | |
| 1,5 hari | 16 | 16 | |
| 2 hari | 32 | ¼×32=8 | 24 |
| 2,5 hari | 48 | 48 | |
| 3 hari | 96 | 96 |
Jadi, banyaknya bakteri setelah 3 hari adalah 96 bakteri (C).
Perdalam materi ini di Pembahasan Matematika UN: Barisan dan Deret.
Soal No. 13 tentang Deret Geometri Tak Hingga
A. 12 m
B. 14 m
C. 16 m
D. 18 m
E. 20 m
Pembahasan
Perhatikan gambar ilustrasi berikut ini!
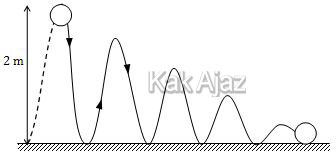
Lintasan bola tersebut membentuk deret geometri tak hingga dengan:
a = 2 m
r = 3/4
Bola mengalami dua lintasan, yaitu lintasan naik dan lintasan turun, kecuali saat pertama kali jatuh (hanya lintasan turun). Sehingga panjang total lintasan sama dengan 2 kali deret tak hingga dikurangi ketinggian awal.

Jadi, jumlah seluruh lintasan bola adalah 14 m (B).
Perdalam materi ini di Pembahasan Matematika UN: Barisan dan Deret.
Soal No. 14 tentang Limit Fungsi

adalah ….
A. 6√2
B. 3√2
C. 0
D. −3√2
E. −6√2
Pembahasan
Limit fungsi di atas lebih mudah dikerjakan dengan menggunakan dalil L’Hopital, caranya hanya dengan menurunkan pembilang dan penyebutnya. Misalkan pembilangnya adalah f(x) dan penyebutnya g(x).
f(x) = 2 + x − x2
f‘(x) = 1 − 2x
g(x) = √x − √2
g’(x) = 1/(2√x)
Dengan demikian,
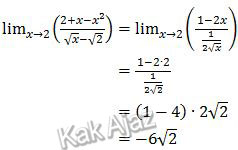
Jadi, nilai dari limit di atas adalah -6√2 (E).
Perdalam materi ini di Pembahasan Matematika UN: Limit Fungsi.
Soal No. 15 tentang Limit Fungsi

adalah ….
A. −4/3 √3
B. −2
C. 0
D. 2
E. 4/3 √3
Pembahasan
Limit di atas bisa kita bawa ke bentuk seperti ini:
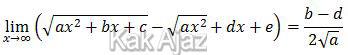
Mari kita selesaikan!
Ini kelihatannya rumit. Padahal sebenarnya cuma perkalian suku seperti (a − b)c = ac − bc.
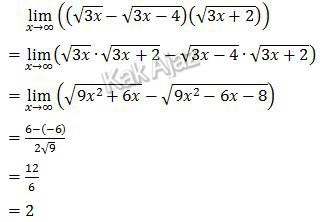
Jadi, nilai dari limit fungsi di atas adalah 2 (D).
Perdalam materi ini di Pembahasan Matematika UN: Limit Fungsi.
Simak Pembahasan Soal Matematika IPA UN 2019 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat