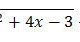pembahasan selanjutnya adalah
- limit fungsi aljabar,
- limit fungsi trigonometri,
- turunan fungsi trigonometri,
- aplikasi turunan, serta
- titik stasioner dan nilai ekstrem.
Soal No. 26 tentang Limit Fungsi Aljabar
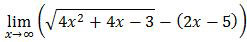
adalah ….
A. −6
B. −4
C. −1
D. 4
E. 6
Pembahasan
Bentuk umum dari limit tersebut adalah:
Limit fungsi pada soal di atas harus diupayakan agar mempunyai bentuk yang sama dengan bentuk umum. Caranya dengan mengubah (2x − 5) menjadi bentuk akar.

Dengan demikian bentuk limit fungsi tersebut menjadi:
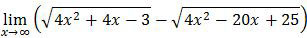
Berdasarkan bentuk umum ini diperoleh:
a = 4
b = 4
c = −3
d = −20
e = 25
Sehingga hasil dari limit tersebut adalah:
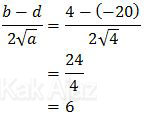
Jadi, nilai dari limit fungsi aljabar tersebut adalah 6 (E).
Perdalam materi ini di Pembahasan Matematika IPA UN: Limit Fungsi.
Soal No. 27 tentang Limit Fungsi Trigonometri
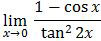
adalah ….
A. 1/8
B. 1/4
C. 1/2
D. 1
E. 2

Pembahasan
Prinsip utama menyelesaikan limit fungsi trigonometri adalah menerapkan bahwa:
sin x = tan x = x
Dengan prinsip tersebut, bentuk kosinus harus diubah menjadi bentuk sinus. Perhatikan rumus cos 2x berikut ini.
cos 2x = 1 − 2 sin2x
Analogi bentuk tersebut diperoleh:
cos x = 1 − 2 sin2 ½x
Sehingga diperoleh:
1 − cos x = 2 sin2 ½x
Dengan demikian, limit fungsi trigonometri di atas dapat diubah menjadi:
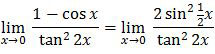
Sekarang bentuknya sudah dalam sinus dan tangens. Kita tinggal menggantinya dengan x saja.
sin2 ½x = (½x)2
tan2 2x = (2x)2
Sehingga diperoleh:
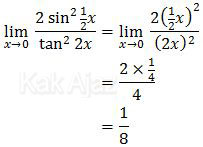
Jadi, nilai dari limit fungsi trigonometri tersebut adalah 1/8 (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Limit Fungsi.
Soal No. 28 tentang Turunan Fungsi Trigonometri
A. f’(x) = 5 cos3 (π − 2x) sin (2π − 4x)
B. f’(x) = 5 cos3 (π − 2x) sin (π − 2x)
C. f’(x) = 5 cos3 (π − 2x) cos (2π − 4x)
D. f’(x) = −5 cos3 (π − 2x) sin (2π − 4x)
E. f’(x) = −5 cos3 (π − 2x) sin (π − 2x)
Pembahasan
Soal di atas adalah turunan berantai. Hal ini karena di dalam fungsi f(x) terdapat 3 fungsi, yaitu fungsi (π − 2x), fungsi kosinus, dan fungsi pangkat 5.
Ketiga fungsi tersebut harus diturunkan satu per satu kemudian dirangkai jadi satu.
turunan (π − 2x) = −2
turunan kosinus = −sin (π − 2x)
turunan pangkat 5 = 5 cos4 (π − 2x)
Sehingga turunan fungsi f(x) adalah:
f’(x) = −2 [−sin (π − 2x)] 5 cos4 (π − 2x)
= 2 sin (π − 2x) . 5 cos4 (π − 2x)
Ternyata pada opsi jawaban tidak ada fungsi kosinus pangkat 4. Rupanya kita diarahkan untuk memecah fungsi kosinus pangkat 4 menjadi pangkat 3 dan pangkat 1. Kemudian fungsi kosinus yang pangkat satu dipadukan dengan fungsi sinus sesuai dengan rumus:
2 sin A cos A = sin 2A
Dengan demikian, turunan fungsi f(x) tersebut dapat dilanjutkan menjadi:
f’(x) = 2 sin (π − 2x) . 5 cos3 (π − 2x) cos (π − 2x)
= 5 cos3 (π − 2x) . 2 sin (π − 2x) cos (π − 2x)
= 5 cos3 (π − 2x) sin 2(π − 2x)
= 5 cos3 (π − 2x) sin (2π − 4x)
Jadi, turunan pertama dari fungsi trigonometri tersebut adalah opsi (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Turunan Fungsi.
Soal No. 29 tentang Aplikasi Turunan Fungsi
A. y = 5x + 5
B. y = 5x − 3
C. y = 5x − 17
D. y = 4x + 3
E. y = 4x − 3
Pembahasan
Persamaan umum garis singgung adalah:
y − y1 = m(x − x1)
dengan x1 dan y1 berturut-turut adalah absis dan ordinat titik singgung. Pada soal diketahui absis x1 = 2. Ordinatnya dapat dicari dengan substitusi absis pada kurva y.
y = 2x2 − 3x + 5
y1 = 2×22 − 3×2 + 5
= 8 − 6 + 5
= 7
Sedangkan m adalah gradien garis singgung. Gradien garis singgung merupakan turunan fungsi y. Nilai m dapat ditentukan dengan substitusi absis x = 2.
y = 2x2 − 3x + 5
m = y‘
= 4x − 3
= 4×2 − 3
= 8 − 3
= 5
Dengan demikian, persamaan garis singgung kurva y adalah:
y − y1 = m(x − x1)
y − 7 = 5(x − 2)
y − 7 = 5x − 10
y = 5x − 3
Jadi, persamaan garis singgung kurva tersebut adalah y = 5x − 3 (B).
Soal No. 30 tentang Titik Stasioner dan Nilai Ekstrem
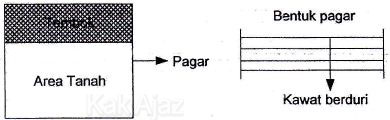
Batas tanah yang dibatasi pagar adalah yang tidak bertembok. Kawat yang tersedia 800 meter. Berapakah luas maksimum yang dapat dibatasi oleh pagar yang tersedia?
A. 80.000 m2.
B. 40.000 m2.
C. 20.000 m2.
D. 5.000 m2.
E. 2.500 m2.
Pembahasan
Kawat berduri 800 meter digunakan sebagai pagar. Sesuai gambar, pagar kawat tersebut terdiri dari 4 lapis. Sehingga keliling pagar tersebut adalah:
K = 800 m : 4
= 200 m
Sekarang perhatikan gambar berikut ini!

Area tanah yang dipagar hanya 3 sisi, yaitu panjang dan 2 kali lebar tanah. Sehingga keliling pagar tersebut adalah:
K = p + 2l
200 = p + 2l
p = 200 − 2l …. (1)
Sementara itu, luas tanah yang dipagar adalah:
L = p . l
Substitusi persamaan (1) ke luas tanah diperoleh:
L = (200 − 2l) . l
= 200l − 2l2
Luas tanah akan maksimum saat L‘ = 0.
L‘ = 0
200 − 4l = 0
4l = 200
l = 50
Substitusi l = 50 ke persamaan (1) diperoleh:
p = 200 − 2l
= 200 − 2×50
= 100
Dengan demikian, luas maksimum tercapai jika p = 100 m dan l = 50 m.
L = p . l
= 100 × 50
= 5.000
Jadi, luas maksimum yang dapat dibatasi oleh pagar yang tersedia adalah 5.000 m2 (D).
Perdalam materi ini di Pembahasan Matematika IPA UN: Titik Stasioner dan Nilai Ekstrem.
Simak Pembahasan Soal Matematika IPA UN 2016 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat