Pembahasan Matematika IPA UN 2016 No. 21

• aturan sinus dan kosinus, 
• dimensi tiga (jarak titik ke garis), 
• dimensi tiga (sudut antara garis dan bidang), 
• transformasi geometri, serta 
• lingkaran.

Soal No. 21 tentang Aturan Sinus dan Kosinus

Sebuah kapal mulai bergerak dari pelabuhan A pada pukul 07.00 dengan arah 030° dan tiba di pelabuhan B setelah 4 jam bergerak. Pukul 12.00 kapal bergerak kembali dari pelabuhan B menuju pelabuhan C dengan memutar haluan 150° dan tiba di pelabuhan C pukul 20.00. Kecepatan rata-rata kapal 50 mil/jam.

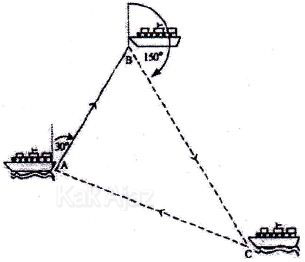
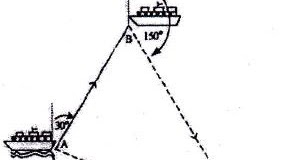
Jarak tempuh kapal dari pelabuhan C ke pelabuhan A adalah ….

A.   200√2 mil
B.   200√3 mil
C.   200√6 mil
D.   200√7 mil
E.   600 mil

Pembahasan

Diketahui:

t_AB = 4 jam
t_BC = 20.00 − 12.00
      = 8 jam
  v  = 50 mil/jam

Jarak tempuh dari pelabuhan A ke pelabuhan B adalah:

s_AB = v . t_AB
       = 50 mil/jam × 4 jam
       = 200 mil

Sedangkan jarak tempuh dari pelabuhan B ke pelabuhan C adalah:

s_BC = v . t_BC
       = 50 mil/jam × 8 jam
       = 400 mil

Perhatikan perjalanan kapal berikut ini!

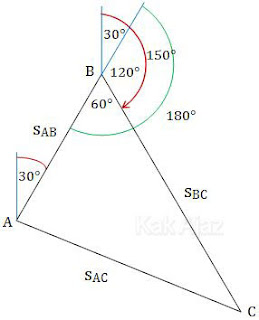
Berdasarkan gambar di atas, jarak tempuh kapal dari pelabuhan C ke pelabuhan A (s_AC) dapat ditentukan dengan aturan kosinus segitiga.

s_AC² = s_AB² + s_BC² − 2 . s_AB . s_BC . cos B
        = 200² + 400² − 2 × 200 × 400 cos 60°
        = 40.000 + 160.000 − 80.000
        = 120.000
 s_AC = 200√3

Jadi, jarak tempuh kapal dari pelabuhan C ke pelabuhan A adalah 200√3 mil (B).

Simak soal sejenis di Pembahasan Matematika IPA UN 2017 No. 25
Perdalam materi ini di Pembahasan Matematika IPA UN: Aturan Sinus dan Kosinus.

Soal No. 22 tentang Dimensi Tiga (jarak titik ke garis)

Pembahasan

Perhatikan gambar kubus ABCD.EFGH berikut ini!

AC adalah diagonal bidang, sedangkan AO adalah setengah diagonal AC.

AC = a√2
      = 8√2

AO = ½ AC
       = ½ × 8√2
       = 4√2

Jarak titik E ke garis BD adalah garis EO. Pandanglah segitiga AOE.

Jadi, jarak dari titik E ke garis BD adalah 4√6 cm (D).

Perdalam materi ini di Pembahasan Matematika IPA UN: Jarak Titik, Garis, dan Bidang [Dimensi Tiga].

Soal No. 23 tentang Dimensi Tiga (sudut antara garis dan bidang)

Pembahasan

Perhatikan terbentuknya sudut antara garis AH dan bidang BDHF berikut ini!

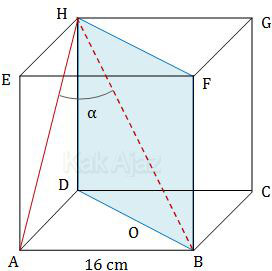
Garis AH dan bidang BDHF bertemu di titik H. Dari titik H ini ditarik garis pertolongan hingga terbentuk sudut α.

Garis AH adalah diagonal bidang.

AH = a√2
       = 16√2

Sedangkan garis HB adalah diagonal ruang.

HB = a√3
      = 16√3

Cara I: Aturan Kosinus Segitiga

Pandanglah segitiga ABH! Sudut α dapat dicari dengan menggunakan aturan kosinus.

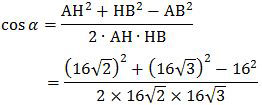
Jika masing-masing suku ruas kanan dibagi dengan 16² maka diperoleh:

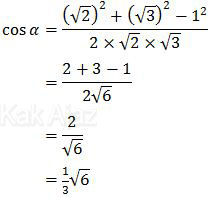
Sayang sekali pertanyaannya sin α. Sabar sedikit, ya. Tinggal satu langkah lagi. Kita buat perbandingan trigonometri dengan memanfaatkan sifat segitiga siku-siku.

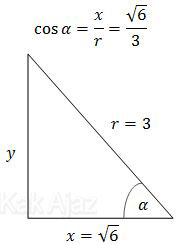
Nilai y pada segitiga siku-siku di atas adalah:

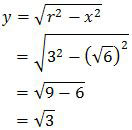
Dengan demikian, nilai dari sin α adalah:

Cara II: Segitiga Siku-siku

Jika Anda jeli, segitiga ABH adalah segitiga siku-siku di A.

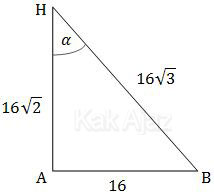
Dengan demikian, nilai sin α adalah:

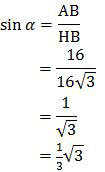
Jadi, nilai sinus sudut antara garis AH dengan bidang BDHF adalah ⅓√3 (B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Sudut antara Garis dan Bidang [Dimensi Tiga].

Soal No. 24 tentang Transformasi Geometri

Pembahasan

Mencerminkan terhadap sumbu x dilanjutkan dengan mencerminkan terhadap sumbu y sama saja dengan mencerminkan terhadap pangkal koordinat atau memutar 180°. Sehingga bayangan dan benda akan saling bertolak belakang. Secara matematis dapat dinotasikan:

(x, y) → (−x, −y)

Sehingga diperoleh:

x‘ = −x   atau   x = −x‘  … (1)
y‘ = −y   atau   y = −y‘  … (2)

Persamaan bayangan kurva y diperoleh dengan cara substitusi persamaan (1) dan (2) pada kurva y.

kurva      :    y = 3x² + 2x − 1
bayangan: −y’ = 3(−x‘)² + 2(−x‘) − 1
                        = 3(x‘)² − 2x‘ − 1
                     y‘ = −3(x‘)² + 2x‘ + 1

Jadi, persamaan bayangan kurva tersebut adalah y = −3x² + 2x + 1 (C B).

Perdalam materi ini di Pembahasan Matematika IPA UN: Transformasi Geometri.

Soal No. 25 tentang Lingkaran

Pembahasan

Persamaan garis singgung lingkaran yang sejajar atau tegak lurus suatu garis dirumuskan sebagai:

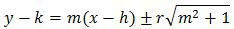
dengan (h, k) adalah pusat lingkaran, r adalah jari-jari lingkaran, dan m adalah gradien garis singgung.

Kita tentukan dulu pusat dan jari-jari lingkaran dengan cara membandingkan dengan bentuk umumnya.

x² + y² + Ax + By + C = 0
x² + y² + 2x − 4y − 15 = 0

Dengan membandingkan bentuk umumnya diperoleh:

A = 2
B = −4
C = −15

Adapun pusat dan jari-jari lingkaran dirumuskan:

pusat: (−½A, −½B)
           (−½×2, −½×(−4))
           (−1, 2)

jari-jari:

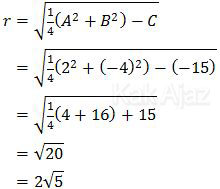
Garis singgung lingkaran sejajar dengan garis 2x + y + 3 = 0, berarti gradien garis singgung sama dengan gradien garis tersebut.

Gradien garis ax + by + c = 0 dirumuskan:

m = −a/b

Sehingga gradien garis 2x + y + 3 = 0 adalah:

m = −2/1
    = −2

Dengan demikian, persamaan garis singgung lingkaran tersebut adalah:

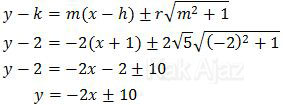
Sekarang tinggal menguraikan nilai plus dan minus pada persamaan tersebut

y = −2x + 10
2x + y −10 = 0

dan

y = −2x − 10
2x + y +10 = 0

Jadi, salah satu persamaan garis singgung lingkaran adalah 2x + y + 10 = 0 (A).

Perdalam materi ini di Pembahasan Matematika IPA UN: Lingkaran.

Simak Pembahasan Soal Matematika IPA UN 2016 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih