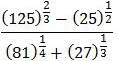pembahasan selanjutnya adalah
- perpangkatan,
- bentuk akar,
- logaritma,
- pertidaksamaan logaritma, dan
- persamaan kuadrat.
Soal No. 1 tentang Perpangkatan
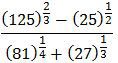
adalah ….
A. 8/3
B. 10/3
C. 14/3
D. 16/3
E. 20/3
Pembahasan
Kita kerjakan per suku saja supaya agak santai.
(125)2/3 = (53)2/3
= 52
= 25
(25)1/2 = (52)1/2
= 51
= 5
(81)1/4 = (34)1/4
= 31
= 3
(27)1/3 = (33)1/3
= 31
= 3
Dengan demikian, bentuk bilangan berpangkat tersebut dapat disederhanakan menjadi:
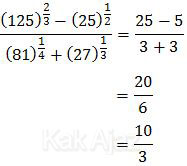
Jadi, nilai dari perpangkatan tersebut adalah 10/3 (B).
Perdalam materi ini di Pembahasan Matematika IPA UN: Perpangkatan.
Soal No. 2 tentang Bentuk Akar
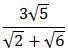
adalah ….
A. ¾√30 + √10
B. ¾√30 + ¾√10
C. ¾√30 − ¾√10
D. ¾√10 − ¾√30
E. −¾√10 − ¾√30

Pembahasan
Langkah pertama adalah mengalikan pembilang dan penyebut bentuk akar tersebut dengan bilangan sekawan dari penyebut, yaitu √2 − √6.
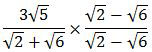
Pada perkalian di atas, bagian pembilang langsung bisa dikalikan, sedangkan bagian penyebut harus mengingat rumus:
(a + b)(a − b) = a2 − b2
sehingga diperoleh:
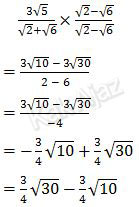
Jadi, bentuk sederhana dari bentuk akar tersebut adalah ¾√10 − ¾√30 ¾√30 − ¾√10 (DC).
Perdalam materi ini di Pembahasan Matematika IPA UN: Bentuk Akar.
Soal No. 3 tentang Logaritma

adalah ….
A. 121/4
B. 81/4
C. 25/4
D. 6
E. 1/2
Pembahasan
Kita ubah angka-angka yang terlalu besar ke dalam bentuk pangkat, seperti:
27 = 33
81 = 34
8 = 23
4 = 22
Sehingga bentuk logaritma tersebut menjadi:
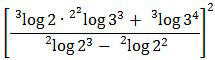
Selanjutnya kita gunakan rumus-rumus logaritma berikut ini untuk menyelesaikannya.
alog xn = n alog x
amlog xn = n/m alog x
Dengan demikian, diperoleh:
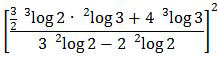
Dengan memanfaatkan rumus:
alog a = 1
alog b . blog a = alog a
diperoleh:

Jadi, nilai dari bentuk logaritma tersebut adalah 121/4 (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Logaritma.
Soal No. 4 tentang Pertidaksamaan Logaritma
1/3log (x + √3)
adalah ….
A. x < −√3 atau 0 < x < 2
B. −2 < x < −√3 atau √3 < x < 2
C. √3 < x < 2
D. −2 < x < 2
E. −√3 < x < 2
Pembahasan
Langkah pertama adalah mengubah bilangan 0 menjadi bentuk logaritma (0 = log 1).
1/3log (x + √3) + 1/3log (x − √3) > 1/3log 1
Kemudian kita gunakan rumus [log a + log b = log ab] untuk menyederhanakan bentuk.
1/3log [(x + √3)(x − √3)] > 1/3log 1
Selanjutnya kita sederhanakan lagi dengan memanfaatkan rumus [(a + b)(a − b) = a2 − b2].
1/3log (x2 − 3) > 1/3log 1
Nah, kalau bentuk sudah seperti di atas, kita tinggal coret saja logaritmanya. Tapi ingat, karena bilangan pokoknya 1/3 maka tanda pertidaksamaannya harus diubah.
x2 − 3 < 1
x2 − 4 < 0
(x + 2)(x − 2) < 0
Karena tanda pertidaksamaannya ‘<‘ maka hasil penyelesaian bentuk kuadrat tersebut berada di antara −2 dan 2.
−2 < x < 2 … (1)
Meskipun hasil ini ada di opsi jawaban, jangan terkecoh. Ini belum selesai. Soal pertidaksamaan logaritma mengandung syarat yang harus diperhitungkan.
Ingat, bilangan yang di-log harus positif. Sehingga syaratnya adalah:
x + √3 > 0
x > −√3 … (2)
x − √3 > 0
x > √3 … (3)
Penyelesaian akhirnya, kita buat garis bilangan dari pertidaksamaan (1), (2), dan (3).

Jadi, nilai x dari pertidaksamaan logaritma tersebut adalah √3 x
Perdalam materi ini di Pembahasan Matematika UN: Pertidaksamaan Eksponen dan Logaritma.
Soal No. 5 tentang Persamaan Kuadrat
A. 5 dan −11
B. −5 dan 11
C. 5 dan 11
D. −5 dan 6
E. 5 atau 6
Pembahasan
Berdasarkan pertidaksamaan di atas diketahui:
a = 1
b = −(p + 3)
c = 12
Kita gunakan rumus penjumlahan dan perkalian akar-akar persamaan kuadrat.
α.β = c/a
3β.β = 12
β2 = 4
β = ±2
α + β = −b/a
3β
4β = p + 3
p = 4β − 3
Substitusi β = ±2 diperoleh:
p = 4 × 2 − 3
= 8 − 3
= 5
p = 4 × (−2) − 3
= −8 − 3
= −11
Jadi, nilai p yang memenuhi adalah 5 dan −11 (A).
Perdalam materi ini di Pembahasan Matematika IPA UN: Persamaan dan Fungsi Kuadrat.
Simak Pembahasan Soal Matematika IPA UN 2016 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat