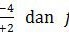Pembahasan Matematika Dasar No. 6

By Posted on

pembahasan selanjutnya adalah

Pembahasan soal Tes Kemampuan dan Potensi Akademik (TKPA) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2014 kode naskah 642 mata uji Matematika Dasar nomor 6 sampai dengan nomor 10 tentang:

  • komposisi dan invers fungsi, 
  • statistika, 
  • logaritma, 
  • fungsi kuadrat, serta 
  • turunan fungsi.

Soal No. 6 tentang Komposisi dan Invers Fungsi

Jika

Fungsi g(x-2) dan f(x)

maka (f ∘ g−1)(2) = ….

A.   103
B.   104
C.   130
D.   134
E.   143



Pembahasan

Langkah pertama adalah mengubah fungsi g(x − 2) menjadi fungsi g(x). Caranya dengan memanipulasi x − 4 dan x + 2 sebagai berikut: 

x − 4 = x − 2 − 2 
x + 2 = x − 2 + 4

sehingga diperoleh:

Mengubah fungsi g(x-2) menjadi g(x)

Selanjutnya, kita tentukan invers fungsi g(x) dengan menggunakan rumus

Rumus invers fungsi dalam bentuk pecahan linear

Berdasarkan rumus tersebut diperoleh:

Invers fungsi g(x)

Nilai invers fungsi g untuk x = 2 adalah:

Nilai invers fungsi g untuk x = 2
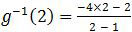
                = −10

Dengan demikian, nilai dari (f ∘ g−1)(2) adalah:

(f ∘ g−1)(2) = f [g−1(2)]
                   = f (−10)
                   = (−10)2 + 3    [f(x) = x2 + 10]
                   = 100 + 3
                   = 103

Jadi nilai dari (f ∘ g−1)(2) adalah 103 (A).

Soal No. 7 tentang Statistika

Tiga puluh data mempunyai rata-rata p. Jika rata-rata 20% data di antaranya adalah p + 0,1, 40% data lainnya adalah p − 0,1, 10% lainnya lagi adalah p − 0,5. Dan rata-rata 30% data sisanya adalah p + q maka q = ….

A.   1/5
B.   7/30
C.   4/15
D.   3/10
E.   1/3

Ebook Pembahasan Soal SBMPTN

Pembahasan

Data-data yang diketahui pada soal:

  n = 30
  x = p
n1 = 20% × 30 = 6 
x1 = p + 0,1 
n2 = 40% × 30 = 12 
x2 = p − 0,1 
n3 = 10% × 30 = 3 
x3 = p − 0,5 
n4 = 30% × 30 = 9 
x4 = p + q
 
Kita gunakan rumus rata-rata gabungan untuk menyelesaikan soal di atas.

Rumus rata-rata gabungan
30p = 6p + 0,6 + 12p − 1,2 + 3p − 1,5 + 9p + 9q 
30p = 30p + 0,6  − 2,1 + 9q
  9q = 2,1
    q = 2,1/9
       = 21/90
       = 7/30

Jadi, nilai q pada data tersebut adalah 7/30 (B).

Soal No. 8 tentang Logaritma

Jika p = (alog ⁡2)(a2blog ⁡4) maka 1/p = ….

A.   22log ⁡a + 2log ⁡√a 2log ⁡b
B.   22log ⁡a + ½ 2log (⁡ab)
C.   (2log ⁡a)2 + ½ 2log ⁡a 2log ⁡b
D.   (2log ⁡a)2 + ½ 2log (⁡ab)
E.   (2log ⁡a)2 + ½ 2log ⁡⁡√ab



Pembahasan

Mari kita selesaikan soal di atas dengan cermat dan hati-hati.

   p = alog ⁡2 . a2blog ⁡4
1/p = 2log a . 4log ⁡a2b                [tinggal dibalik]
      = 2log a (4log ⁡a2 + 4log b)    [log ab = log a + log b]
      = 2log a (22log ⁡a2 + 22log b)
      = 2log a (2log ⁡a + ½ 2log b)   [anlog bm = m/n alog ⁡b]
      = (2log ⁡a)2 + ½ 2log ⁡a 2log ⁡b
 
Jadi, nilai 1/p dari bentuk logaritma tersebut adalah opsi (C).

Soal No. 9 tentang Fungsi Kuadrat

Fungsi kuadrat f(x) = x2 + 2px + p mempunyai nilai minimum −p dengan p ≠ 0. Jika sumbu simetri kurva f adalah x = a maka nila a + f(a) = ….

A.   6
B.   4
C.   −4
D.   −5
E.   −6

Pembahasan

Koefisien fungsi kuadrat f(x) = x2 + 2px + p adalah: 

a = 1 
b = 2p 
c = p

Sumbu simetri kurva f adalah x = a, diperoleh:

Sumbu simetri kurva f
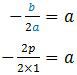
         a = −p
 
Fungsi kuadrat f mempunyai nilai minimum −p. Sedangkan nilai minimum terjadi saat x = a (sumbu simetri) sehingga diperoleh:

              f(a) = −p
a2 + 2pa + p = −p
p2 − 2p2 + p = −p      [substitusi a = −p]
      −p2 + 2p = 0
        p2 − 2p = 0
       p(p − 2) = 0  
p = 0 (tidak memenuhi) atau p = 2

Dengan demikian, 

a + f(a) = −p + (−p)
             = −2p
             = −2×2
             = −4


Jadi, nilai dari a + f(a) adalah −4 (C).

Soal No. 10 tentang Turunan Fungsi

Jika m dan n bilangan real dan fungsi f(x) = mx3 + 2x2 − nx + 5 memenuhi f’(1) = f’(−5) = 0 maka 3m − n = ….

A.   −6
B.   −4
C.   −2
D.   2
E.   4



Pembahasan

Mari kita turunan fungsi f(x) di atas! 

f(x) = mx3 + 2x2 − nx + 5 
f’(x) = 3mx2 + 4x − n

Turunan fungsi tersebut memenuhi f’(1) = f’(−5) = 0. Ambil saja f’(1) = 0.

                     f’(1) = 0
3m×12 + 4×1 − n = 0
          3m + 4 − n = 0
                 3m − n = −4

Jadi, nilai dari 3m − n adalah −4 (B).

Pembahasan Matematika Dasar No. 1 – 5 TKD Saintek SBMPTN 2014
Pembahasan Matematika Dasar No. 11 – 15 TKD Saintek SBMPTN 2014

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih

Semoga Bermanfaat

Related posts: