pembahasan selanjutnya adalah
Soal tentang Sudut antara Garis dan Bidang UN 2011
A. ⅓√6
B. ½√3
C. ½√2
D. ⅓√3
E. ⅓√2
Pembahasan
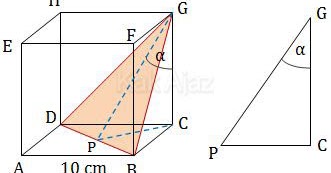
Perhatikan sudut yang dibentuk oleh garis GC dan bidang BDG berikut ini!
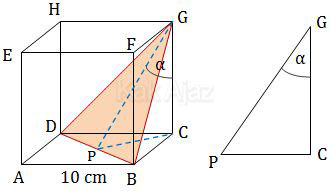
Garis GC dan bidang BDG bertemu di titik G. Dari titik G kita tarik garis melalui pertengahan bidang BDG sampai bidang alas hingga terbentuk segitiga PCG.
Sudut yang dibentuk oleh garis PG dan CG inilah sudut yang ditanyakan.
Segitiga PCG adalah segitiga siku-siku di C. Panjang sisinya adalah sebagai berikut:
CG merupakan rusuk kubus.
CG = a
= 10 cm
PC adalah setengah diagonal bidang.
PC = ½ a√2
= ½ × 10√2
= 5√2
Sedangkan PG adalah sisi miring segitiga PCG sehingga dapat ditentukan dengan teorema Pythagoras.
PG = √(PC2 + CG2)
= √[(5√2)2 + 102]
= 5√[(√2)2 + 22]
= 5√(2 + 4)
= 5√6
Dengan demikian, kosinus α pada segitiga PCG adalah:
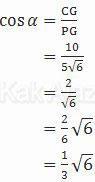
Jadi, kosinus sudut antara garis GC dan bidang BDG adalah ⅓√6 (A).
Soal tentang Sudut antara Garis dan Bidang UN 2012
A. ½√2
B. ½√3
C. ⅓√3
D. ⅔√2
E. ¾√3

Pembahasan
Perhatikan sudut antara AE dan AFH dalam kubus ABCD.EFGH berikut!
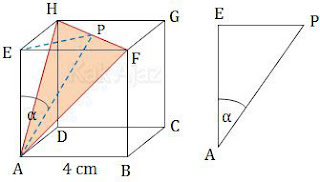
Garis AE dan bidang AFH bertemu di titik A. Dari titik A di buat segitiga AEP melalui pertengahan bidang AFH.
α adalah sudut yang dibentuk oleh garis AE dan AP.
Segitiga AEP adalah segitiga siku-siku di E. Panjang sisi-sisinya adalah sebagai berikut:
AE adalah rusuk kubus.
AE = a
= 4 cm
EP adalah setengah diagonal bidang.
EP = ½ a√2
= ½ × 4√2
= 2√2
Sedangkan AP adalah sisi miring segitiga AEP sehingga dapat ditentukan dengan teorema Pythagoras.
AP = √(AE2 + EP2)
= √[42 + (2√2)2]
= 2√[22 + (√2)2]
= 2√(4 + 2)
= 2√6
Dengan demikian, sinus α pada segitiga AEP adalah:

Jadi, nilai sinα yang dibentuk oleh garis AE dan bidang AFH adalah ⅓√3 (C).
Soal tentang Sudut antara Bidang dan Bidang UN 2015
A. ⅓
B. ½√2
C. ⅔√2
D. √2
E. 2√2
Pembahasan
Perhatikan sudut antara bidang AFH dan bidang CFH dalam kubus ABCD.EFGH berikut!
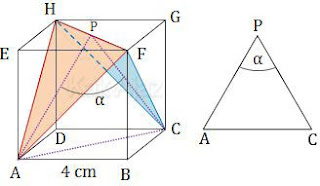
Bidang AFH dan bidang CFH bertemu pada garis FH. Dari pertengahan garis FH (titik P), kita buat segitiga PAC melalui pertengahan bidang AFH dan CFH.
Sudut yang dibentuk oleh garis AP dan CP adalah sudut antara bidang AFH dan CFH.
Sekarang perhatikan segitiga PAC. Segitiga PAC adalah segitiga sama kaki. Panjang sisi-sisinya adalah sebagai berikut:
AC adalah diagonal bidang.
AC = a√2
= 4√2 cm
AP = PC. Garis AP merupakan sisi miring segitiga siku-siku AEP.
AP = √(AE2 + EP2)
= √[42 + (2√2)2]
= 2√[22 + (√2)2]
= 2√(4 + 2)
= 2√6
Sudut α dapat ditentukan dengan aturan kosinus segitiga.
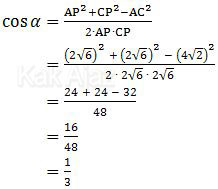
Sekarang kita gunakan trigonometri segitiga untuk mendapatkan nilai dari tangen α.
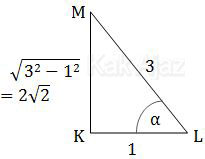
Berdasarkan trigonometri segitiga tersebut, diperoleh:
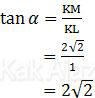
Jadi, tangen sudut antara bidang AFH dengan bidang CFH adalah 2√2 (E).
Catatan:
Pada pembahasan di atas, tertulis rusuknya 4 cm (seharusnya 12 cm sesuai yang tersaji pada soal). Namun karena pertanyaannya adalah sudut, maka berapapun rusuknya tidak akan memengaruh hasil.
Thanks to Naufal Ramadhani.
Soal tentang Sudut antara Bidang dan Bidang UN 2013
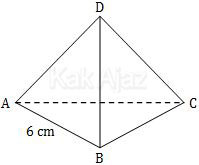
Nilai kosinus sudut antara bidang ABC dan ABD dari gambar bidang empat di atas adalah ….
A. 1/10
B. 1/10 √10
C. 1/3
D. 1/4 √2
E. 2/3 √2
Pembahasan
Gambar pada soal di atas adalah bidang empat beraturan yang tersusun dari empat segitiga sama sisi.
Perhatikan sudut yang bentuk oleh bidang ABC dan ABD di bawah ini.
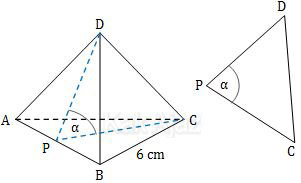
Bidang ABC dan ABD bertemu di titik AB. Dari titik tengah AB (titik P) kita buat segitiga PCD yang melalui pertengahan bidang ABC dan ABD.
Panjang PD = PC. Garis PD merupakan garis tinggi segitiga sama sisi yang dirumuskan:
t = ½ s√3
PD = ½ × 6√3
= 3√3
Sudut α dapat ditentukan dengan aturan kosinus sebagai berikut:
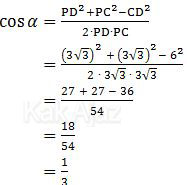
Jadi, nilai kosinus sudut antara bidang ABC dan ABD pada bidang empat tersebut adalah 1/3 (C).
Soal tentang Sudut antara Garis dan Bidang UN 2010
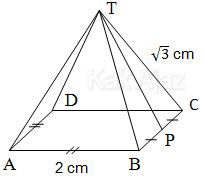
Nilai kosinus sudut antara TP dan bidang alas adalah ….
A. √2
B. ½√3
C. ⅓√6
D. ½√2
E. ⅓√3
Pembahasan
Perhatikan sudut antara TP dan bidang alas pada limas T.ABCD berikut ini!
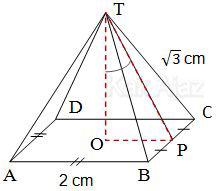
OP adalah setengah rusuk alas.
OP = ½ AB
= ½ × 2 cm
= 1 cm
Pandang segitiga PCT. Garis PT adalah salah satu sisi tegak segitiga tersebut sehingga dapat dicari dengan teorema Pythagoras.
PT = √(CT2 − PC2)
= √[(√3)2 − 12]
= √(3 − 1)
= √2
Sekarang pandang segitiga TOP.
OT = √(PT2 − OP2)
= √[(√2)2 − 12]
= √(2 − 1)
= 1
Nah, sekarang kosinus α sudah dapat ditentukan.
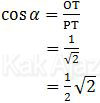
Jadi, nilai kosinus sudut antara TP dan bidang alas adalah ½√2 (D).
Pembahasan soal tentang Sudut antara Garis dan Bidang yang lain bisa disimak di:
Pembahasan Matematika IPA UN 2013 No. 24
Pembahasan Matematika IPA UN 2014 No. 23
Pembahasan Matematika IPA UN 2015 No. 25
Pembahasan Matematika IPA UN 2016 No. 23
Pembahasan Matematika IPA UN 2017 No. 29
Pembahasan Matematika IPA UN 2017 No. 32
Pembahasan Matematika IPA UN 2018 No. 26
Simak juga, Pembahasan Matematika IPA UN: Jarak Titik, Garis, dan Bidang [Dimensi Tiga].
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat