pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPS nomor 1 sampai dengan nomor 5 tentang:
- eksponen,
- logaritma,
- fungsi,
- komposisi fungsi, dan
- invers fungsi.
Soal No. 1 tentang Eksponen

adalah ….
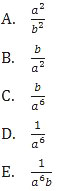
Pembahasan
Langkah pertama, masing-masing faktor dikuadratkan dulu.
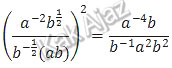
Kemudian, yang berpangkat negatif dipindah posisi (pembilang ke penyebut atau sebaliknya) sehingga pangkatnya menjadi positif. Selanjutnya tinggal menyelesaikan.
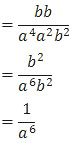
Jadi, nilai bilangan berpangkat di atas adalah opsi (D).
Soal No. 2 tentang Logaritma
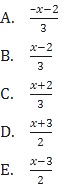
Pembahasan
Angka 8 dan 12 pada 8log 12 diuraikan terlebih dahulu.
8log 12 = 23log (4 . 3)
Setelah itu gunakan rumus anlog b = 1/n alog b dan alog bc = alog b + alog c.
= ⅓ 2log (4 . 3)
= ⅓ (2log 4 + 2log 3)
= ⅓ (2 + x)
= ⅓ (x + 2)
Jadi, nilai dari logaritma tersebut adalah opsi (C).
Soal No. 3 tentang Fungsi
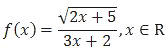
adalah ….


Pembahasan
Daerah asal suatu fungsi merupakan syarat keabsahan fungsi tersebut. Karena fungsi f(x) di atas mengandung bentuk akar maka harus memenuhi syarat akar (yang diakar harus lebih atau sama dengan nol).
2x + 5 ≥ 0
2x ≥ −5
x ≥ −5/2
Selain itu, fungsi f(x) di atas berbentuk pecahan sehingga harus memenuhi syarat penyebut, yaitu penyebut tidak boleh sama dengan nol.
3x + 2 ≠ 0
3x ≠ −2
x ≠ −2/3
Jadi, daerah asal fungsi tersebut adalah opsi (C).
Soal No. 4 tentang Komposisi Fungsi
| A. | (f ∘ g)(x) = 8x2 − 8x − 48 |
| B. | (f ∘ g)(x) = 8x2 − 8x +48 |
| C. | (f ∘ g)(x) = 8x2 − 8x −50 |
| D. | (f ∘ g)(x) = 8x2 − 8x +50 |
| E. | (f ∘ g)(x) = 8x2 + 8x − 50 |
Pembahasan
Fungsi komposisi (f ∘ g)(x) atau f(g(x)) adalah fungsi g(x) dimasukkan ke fungsi f(x).
f(x) = 8x − 2
f(g(x)) = 8g(x) − 2
= 8(x2 − x − 6) − 2
= 8x2 − 8x − 48 − 2
= 8x2 − 8x −50
Jadi, fungsi komposisi (f ∘ g)(x) adalah opsi (C).
Soal No. 5 tentang Invers Fungsi

Invers dari fungsi f(x) adalah ….

Pembahasan
Invers fungsi yang berbentuk pecahan linear dirumuskan sebagai:
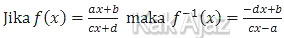
Dengan demikian,

Jadi, invers dari fungsi tersebut adalah opsi (D).
Simak Pembahasan Soal Matematika IPS UN 2018 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
