Pembahasan Matematika IPS UN 2018 No. 6

Pembahasan soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPS nomor 6 sampai dengan nomor 10 tentang:

• fungsi kuadrat, 
• akar persamaan kuadrat, 
• persamaan kuadrat baru, 
• persamaan linear, dan 
• sistem persamaan linear.

Soal No. 6 tentang Fungsi Kuadrat

Perhatikan grafik fungsi kuadrat berikut!

Persamaan fungsi kuadrat dari grafik di atas adalah ….

A.   y = x² − x − 4
B.   y = x² − 2x − 4
C.   y = x² + x − 4
D.   y = 2x² − 2x − 4
E.   y = 2x² + 2x − 4

Pembahasan

Pembuat nol grafik fungsi tersebut adalah (−1, 0) dan (2, 0) sehingga:

y = a(x + 1)(x − 2)
y = a(x² − x − 2) … (1)

Grafik tersebut melalui titik (0, −4). Kita substitusikan titik (0, −4) ke persamaan (1) untuk mendapatkan nila a.

−4 = a(0² − 0 − 2)
−4 = −2a
  a = 2

Nah, tinggal ke substitusikan a = 2 ke persamaan (1).

y = 2(x² − x − 2)
   = 2x² − 2x − 4

Jadi, persamaan fungsi kuadrat dari grafik di atas adalah opsi (D).

Soal No. 7 tentang Akar Persamaan Kuadrat

Pembahasan

Persamaan x² − (a + 2)x + a = 0 mempunyai nilai:

a = 1
b = −(a + 2)
c = a

Penjumlahan dan perkalian akar-akarnya adalah:

p + q = −b/a
         = a + 2

p ∙ q = c/a
        = a

Diketahui p² + q² = 28.

(p + q)² = p² + q² + 2pq
(a + 2)² = 28 + 2 ∙ a
a² + 4a + 4 = 28 + 2a
a² + 2a − 24 = 0
(a − 4)(a + 6) = 0
a = 4 atau a = −6

Jadi, nilai a positif yang memenuhi adalah 4 (D).

Soal No. 8 tentang Persamaan Kuadrat Baru

Pembahasan

Jika akar-akar persamaan kuadrat baru sama dengan akar-akar persamaan kuadrat lama ditambah p maka persamaan kuadrat baru dapat diperoleh dengan mengganti x dengan x − p.

Persamaan kuadrat baru pada soal di atas, akar-akarnya masing-masing ditambah 2 sehingga:

Lama : x² − 3x + 5 = 0

Baru : (x − 2)² − 3(x − 2) + 5 = 0
           x² − 4x + 4 − 3x + 6 + 5 = 0
           x² − 7x + 15 = 0

Jadi, persamaan kuadrat baru yang akar-akarnya (α + 2) dan (β + 2) adalah (B).

Soal No. 9 tentang Persamaan Linear

Pembahasan

Biaya minimum per hari:

f(x) = x + 400/x − 20

Sedangkan total biaya minimum selama x hari:

f(x) = (x + 400/x − 20)x
       = x² + 400 − 20x
       = x² − 20x + 400

Jadi, total biaya minimum yang harus dikeluarkan adalah opsi (B).

Soal No. 10 tentang Sistem Persamaan Linear

Diketahui p dan q memenuhi sistem

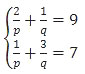
Nilai dari 8p − q adalah ….

A.   7
B.   5/2
C.   1
D.   −1
E.   −5/2

Pembahasan

Misalkan x = 1/p dan y = 1/q maka:

Mari kita eliminasi sistem persamaan linear di atas!

Kita substitusikan x = 4 ke persamaan pertama.

2x + y = 9
  8 + y = 9
        y = 1

Nah, sekarang kita kembalikan ke nilai p dan q.

p = 1/x
   = 1/4

q = 1/y
   = 1

Dengan demikian

8p − q = 8 × 1/4 − 1
           = 2 − 1
           = 1

Jadi, nilai dari 8p − q adalah 1 (C).

Simak Pembahasan Soal Matematika IPS UN 2018 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih