pembahasan selanjutnya adalah

Pembahasan soal Ujian Nasional (UN) tahun 2018 bidang studi Matematika SMA-IPS nomor 11 sampai dengan nomor 15 tentang:
- grafik sistem pertidaksamaan linear,
- model matematika sistem pertidaksamaan linear,
- kesamaan matriks,
- invers matriks, dan
- deret aritmetika.
Soal No. 11 tentang Grafik Sistem Pertidaksamaan Linear



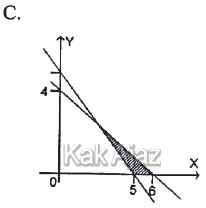
Pembahasan
Kita tentukan dulu garis-garisnya.

Garis (1) melalui titik (0, 6) dan (4,0). Karena tanda pertidaksamaannya “≥” maka daerah yang diarsir berada di atas garis (1).
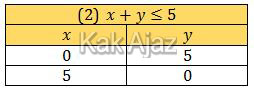
Garis (2) melalui titik (0, 5) dan (5, 0). Karena tanda pertidaksamaannya “≤” maka daerah yang diarsir berada di bawah garis (2).
Sedangkan x ≥ 0 berarti di kanan sumbu y dan y ≥ 0 berarti di atas sumbu x.
Dengan demikian grafiknya adalah:
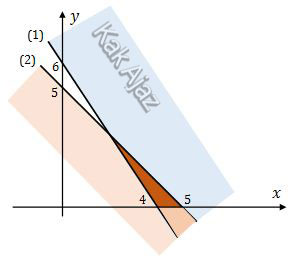
Jadi, grafik yang merupakan penyelesaian sistem pertidaksamaan tersebut adalah opsi (D).
Soal No. 12 tentang Model Matematika Sistem Pertidaksamaan Linear
| A. | 2x + y ≤ 150; x + y ≤ 40; x ≥ 0; y ≥ 0 |
| B. | 2x + y ≤ 150; x + y ≥ 40; x ≥ 0; y ≥ 0 |
| C. | 2x + y ≤ 75; x + y ≥ 40; x ≥ 0; y ≥ 0 |
| D. | 2x + y ≥ 75; x + y ≤ 40; x ≥ 0; y ≥ 0 |
| E. | 2x + y ≤ 75; x + y ≤ 40; x ≥ 0; y ≥ 0 |
Pembahasan
Harga tiket dewasa Rp80.000,00, anak Rp40.000,00, serta jumlah uang tiket Rp3.000.000,00 (tidak lebih yang berarti kurang atau sama dengan 3.000.000).
80.000x + 40.000y ≤ 3.000.000
2x + y ≤ 75
Jumlah tiket tidak boleh melebihi kapasitas gedung (kurang atau sama dengan 40).
x + y ≤ 40
Banyak tiket dewasa dan anak tidak mungkin negatif.
x ≥ 0; y ≥ 0
Jadi, model matematika yang sesuai untuk masalah tersebut adalah opsi (E).
Soal No. 13 tentang Kesamaan Matriks

Jika 3A + BC = DT; (DT = transpose D), nilai dari 2x + 3y − z = ….
A. −18
B. −14
C. −12
D. −8
E. 14

Pembahasan
Kita mulai dari transpose D (baris diganti kolom).
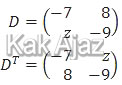
Selanjutnya kita selesaikan kesamaan matriksnya.

Dari kesamaan di atas diperoleh:
z = 13
3x − 4 = −7
3x = −3
x = −1
9 − y = 8
−y = −1
y = 1
Dengan demikian
2x + 3y − z = 2×(−1) + 3×1 − 13
= −2 + 3 − 13
= −12
Jadi, nilai dari 2x + 3y − z adalah −12 (C).
Soal No. 14 tentang Invers Matriks
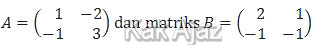
Invers dari matriks AB adalah ….
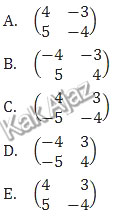
Pembahasan
Mari kita mengingat kembali rumus invers matriks.
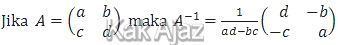
Selanjutnya kita kalikan matriks A dan B kemudian kita inverskan hasil perkaliannya.
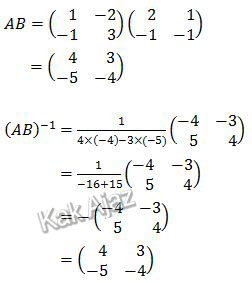
Jadi, invers dari matriks AB adalah opsi (C).
Soal No. 15 tentang Deret Aritmetika
A. Rp500.000,00
B. Rp550.000,00
C. Rp600.000,00
D. Rp700.000,00
E. Rp725.000,00
Pembahasan
Karena uang ayah bertambah secara tetap, maka harus diselesaikan dengan rumus deret aritmetika.
a = 50.000
b = 55.000 − 50.000 = 5.000
n = 10
Jumlah tabungan selama 10 bulan dirumuskan:
Sn = 1/2 n[2a + (n − 1)b]
S10 = 1/2×10[2×50.000 + (10 − 1)×5.000]
= 5(100.000 + 45.000)
= 5 × 145.000
= 725.000
Jadi, jumlah tabungan selama 10 bulan adalah Rp725.000,00 (E)
Simak Pembahasan Soal Matematika IPS UN 2018 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat
