Pembahasan Pengetahuan Kuantitatif No. 61

By Posted on

pembahasan selanjutnya adalah

Semangat menghadapi UTBK, Pembahasan Pengetahuan Kuantitatif No. 61 - 70 TPS UTBK SBMPTN 2019

Pembahasan soal Pengetahuan Kuantitatif Tes Potensi Skolastik (TPS) pada Ujian Tulis Berbasis Komputer (UTBK) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2019 nomor 61 sampai dengan nomor 70 tentang pengetahuan kuantitatif.

Soal No. 61

Di antara berikut ini, bilangan mana yang merupakan a ketika a/3 prima?

Pembahasan

Misal p adalah bilangan prima, maka:

a/3 = p, dengan p = {2, 3, 5, …}
a = 3p

Untuk p = 2, diperoleh:
Jadi, bilangan a adalah 6 (D).

Soal No. 62

Jika 90/k bulat, apakah k bulat?
1) k > 1
2) k merupakan kelipatan bilangan prima

A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
B. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
E. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

Pembahasan

Misal b adalah bilangan bulat maka:

90/k = b

Ambil saja k = 4, diperoleh:

90/4 = 22,5 [bukan bilangan bulat]

k = 4 memenuhi pernyataan (1) dan (2) tetapi tidak menghasilkan bilangan bulat.

Jadi, pernyataan (1) dan (2) tidak cukup untuk menjawab pertanyaan (E).

Soal No. 63

Setiap bilangan berikut bisa merupakan nilai dari 2/(10 − x) kecuali ….

Pembahasan

Bilangan dalam bentuk pecahan akan mempunyai nilai bila penyebutnya tidak sama dengan nol.
Jadi, yang bukan nilai dari bentuk tersebut adalah 10 (E).

Soal No. 64

Jika Marvin menyimpan x/10 dari pendapatan bulanannya untuk tabungan, berapa x?
1) Marvin menyimpan10% dari pendapatannya.
2) Pendapatan Marvin Rp25.000.000 per bulan.

A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
B. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
E. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.
Artkel Terkait  Pembahasan Kimia UN: Unsur Radioaktif

Pembahasan

Misal s adalah simpanan uang Marvin dan p adalah pendapatan bulanannya.

Marvin menyimpan x/10 dari pendapatan bulanannya.

s = x/10 × p … (1)

1) Marvin menyimpan10% dari pendapatannya.

s = 10% × p … (2)

Dari persamaan (1) dan (2) diperoleh:

x/10 × p = 10% × p
x × 0,1 × p = 0,1 × p
x = 1

2) Pendapatan Marvin Rp25.000.000 per bulan.

p = 25.000.000 … (3)

Dari persamaan (1) dan (3) diperoleh:

s = x/10 × p
s = x/10 × 25.000.000

Nilai x tidak mungkin diperoleh hanya dengan pernyataan (2).

Jadi, pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup (A).

Soal No. 65

Berapakah 0,03 dari z?
1) 0,0008 adalah 0.02 dari z.
2) 0,01 dari z adalah 0,0004.

A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
B. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
E. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

Pembahasan

Kita harus mencari nilai z. Jika nilai z bisa dicari maka nilai 0,03 dari z otomatis bisa dicari.

1) 0,0008 adalah 0.02 dari z.
2) 0,01 dari z adalah 0,0004.

Ternyata, baik pernyataan (1) maupun pernyataan (2) bisa digunakan untuk mencari z.

Jadi, pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup (D).

Soal No. 66

Jika x dan y bilangan bulat, 1 xyx/y yang mungkin?
A. −13
B. −25
C. 1
D. 7/4
E. 7

Pembahasan

Kita bagi saja dua pertidaksamaan di atas.

1 < x < 7
3 < y < 4
⎯⎯⎯⎯⎯⎯ :
1/3 < x/y < 7/4

Dapat disimpulkan:

  • nilai x/y berada di antara 1/3 dan 7/4 [opsi D dan E salah]
  • nilai x/y tidak mungkin negatif [opsi A dan B salah]
Artkel Terkait  Rangkuman Materi, Contoh Soal Words Order & Pembahasannya

Jadi, nilai x/y yang mungkin adalah 1 (C).

Soal No. 67

Toko cokelat hanya menjual dua jenis batang cokelat, satu seharga Rp30.000,00 dan lainnya Rp70.000,00. Jika kemarin ada 30 pelanggan dan setiap pelanggan membeli tepat 1 batang cokelat, berapa batang Rp70.000,00 yang terjual kemarin?
1) Toko tersebut mendapatkan jumlah uang yang sama untuk penjualan batang Rp30.000,00 maupun Rp70.000,00 kemarin.
2) Toko tersebut mendapatkan Rp1.000.000,00 dari batang cokelat kemarin.

A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
B. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
E. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

Pembahasan

Misal x batang coklat yang berharga Rp30.000,00 dan y adalah batang coklat yang berharga Rp70.000,00.

Ada 30 pelanggan dan setiap pelanggan membeli tepat 1 batang cokelat.

x + y = 30 … (1)

1) Toko tersebut mendapatkan jumlah uang yang sama untuk penjualan batang Rp30.000,00 maupun Rp70.000,00 kemarin.
30.000 x = 70.000y
3x = 7y
3x − 7y = 0 … (2)

Eliminasi persamaan 3(1) dan (2) diperoleh:

3x + 3y = 90
3x − 7y =
⎯⎯⎯⎯⎯⎯⎯⎯
10y = 90
y = 9

2) Toko tersebut mendapatkan Rp1.000.000,00 dari batang cokelat kemarin.
30.000x + 70.000y = 1.000.000
3x + 7y = 100 … (3)

Eliminasi persamaan (3) dan 3(1) diperoleh:

3x + 7y = 100
3x + 3y = 90
⎯⎯⎯⎯⎯⎯⎯⎯
4y = 10
y = 2,5

Pernyataan (2) memang bisa menghasilkan nilai y tetapi hasilnya pecahan. Padahal setiap pelanggan membeli tepat 1 batang cokelat.

Dengan demikian, hanya pernyataan (1) yang bisa digunakan untuk menjawab pertanyaan.

Jadi, pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup (A).

Soal No. 68

Kuadrat dari hasil jumlah pecahan akar, soal pengetahuan kuantitatif TPS UTBK 2019

Pembahasan

Hasil dari kuadrat jumlah akar

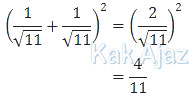
Jadi, nilai dari bentuk tersebut adalah 4/11 (C).

Soal No. 69

Jika x2 + bx + 26 = 8. Berapa b?
1) (x + 9) merupakan salah satu faktor dari x2 + bx + 26 = 8.
2) −2 merupakan salah satu akar dari x2 + bx + 26 = 8.
Artkel Terkait  Awit pamrayogane Begawan Abiyasa, apa kang dilakoni Prabu Pandhu

A. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (2) SAJA tidak cukup.
B. Pernyataan (2) SAJA cukup untuk menjawab pertanyaan, tetapi pernyataan (1) SAJA tidak cukup.
C. DUA pernyataan BERSAMA-SAMA cukup untuk menjawab pertanyaan, tetapi SATU pernyataan SAJA tidak cukup.
D. Pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup.
E. Pernyataan (1) dan pernyataan (2) tidak cukup untuk menjawab pertanyaan.

Pembahasan

1) (x + 9) merupakan salah satu faktor dari x2 + bx + 26 = 8.

(x + 9) adalah faktor sehingga akarnya adalah x = −9.
Nilai b dapat dicari dengan memasukkan x = −9 pada x2 + bx + 26 = 8.

2) −2 merupakan salah satu akar dari x2 + bx + 26 = 8.

Nilai b dapat dicari dengan memasukkan x = −2 pada x2 + bx + 26 = 8.

Dengan demikian, baik pernyataan (1) maupun pernyataan (2) dapat digunakan untuk mencari nilai b.

Jadi, pernyataan (1) SAJA cukup untuk menjawab pertanyaan dan pernyataan (2) SAJA cukup (D).

Soal No. 70

Sebuah lemari memiliki d laci. Setiap laci mengandung h wadah map, dan setiap map mengandung 20 map manila. Berapa map manila yang ada di 3 lemari seperti itu?
A. 30d/h.
B. 30dh.
C. 60/dh.
D. 60dh.
E. 60d/h.

Pembahasan

Banyak map manila (n) merupakan perkalian dari banyak lemari,  banyak laci, banyak wadah map, banyak map manila dalam wadah map.

n = 3 × d × h × 20
= 60dh

Jadi, banyak map manila yang ada di 3 lemari seperti itu adalah 60dh (D).

Simak Pembahasan Soal TPS UTBK SBMPTN 2019 selengkapnya.

PU : Penalaran Umum
PBM : Pemahaman Bacaan dan Menulis
PPU : Pengetahuan dan Pemahaman Umum
PK : Pengetahuan Kuantitatif

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih

Semoga Bermanfaat

Related posts:

Leave a Reply

Your email address will not be published. Required fields are marked *