pembahasan selanjutnya adalah
![Grafik fungsi terigonometri Fungsi Trigonometri dan Grafiknya [Soal UN dan Pembahasan]](https://1.bp.blogspot.com/-mpbm_NMcxQc/XiK_Q7rBaSI/AAAAAAAARI4/OiqSj3gFwOMe5WEWbeOY1O-Up9_uWtBWgCLcBGAsYHQ/s1600/grafik-fungsi-trigonometri.jpg)
Pembahasan soal Ujian Nasional (UN) Matematika SMA-IPA dengan materi pembahasan Fungsi Trigonometri dan Grafiknya yang meliputi:
- grafik fungsi trigonometri dan
- persamaan grafik fungsi trigonometri.
Soal No. 1 tentang Grafik Fungsi Trigonometri



UN 2019
Pembahasan
Kita tentukan pembuat nol-nya dulu.
| y | = | |
| sin 2x | = | |
| 2x | = | 0°, 180°, 360°, … |
| x | = | 0°, 90°, 180°, … |
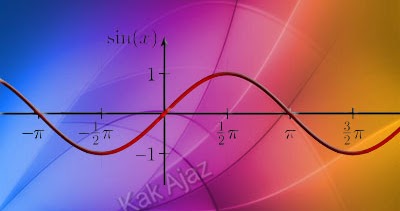
Grafik fungsi sinus dengan pembuat nol di atas adalah:

Jadi, grafik fungsi y = sin 2x adalah grafik pada opsi (C).
Soal No. 2 tentang Grafik Fungsi Trigonometri

Pembahasan
Fungsi f(x) = 2 sin (x − 30)° sudah tampak jelas mempunyai amplitudo 2. [opsi C, D, dan E salah]
Sekarang kita tentukan pembuat nol-nya.
| y | = | |
| 2 sin (x − 30)° | = | |
| sin (x − 30)° | = | |
| x − 30° | = | 0°, 180°, 360°, … |
| x | = | 30°, 210°, 390°, … |
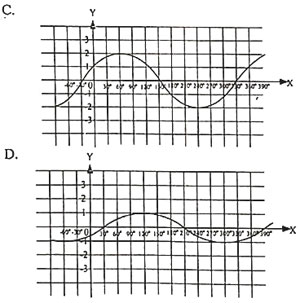
Grafik fungsi sinus dengan pembuat nol di atas adalah:
Jadi, grafik fungsi f(x) = 2 sin (x − 30)° adalah grafik pada opsi (A).
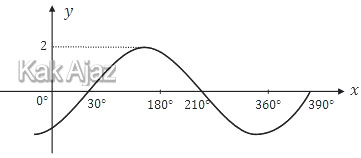
Soal No. 3 tentang Persamaan Grafik Fungsi Trigonometri
Persamaan fungsi trigonometri pada grafik di atas adalah ….
| A. | y = cos (x + 60°) |
| B. | y = cos (x − 60°) |
| C. | y = sin (x + 60°) |
| D. | y = sin (x − 60°) |
| E. | y = −sin (x − 60°) |

Pembahasan
Grafik fungsi trigonometri bisa merupakan grafik sinus maupun kosinus, tergantung fase awalnya.
Perhatikan gambar berikut ini!

Berdasarkan grafik di atas:
| A | = | ±1 |
| ½ T | = | 330° − 150° |
| ½ T | = | 180° |
| T | = | 360° |
| = | 2π |
Bilangan gelombang (k) grafik tersebut adalah:
Jika grafik di atas adalah grafik sinus, fase awalnya adalah θo = 60°, amplitudonya A = 1, dan bilangan gelombang k = 1.
| y | = | A sin k(x − θo) |
| = | 1 sin 1(x − 60°) | |
| = | sin (x − 60) |
Jadi, persamaan fungsi trigonometri pada grafik di atas adalah y = sin(x − 60°) (D).
Soal No. 4 tentang Persamaan Grafik Fungsi Trigonometri
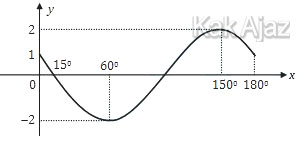
Persamaan grafik fungsi trigonometri pada gambar di atas adalah ….
| A. | y = 2 cos 2(x − 15°) |
| B. | y = −2 sin 2(x − 15°) |
| C. | y = 2 sin 2(x − 15°) |
| D. | y = −2 cos (2x − 15°) |
| E. | y = −2 cos 2(x − 15°) |
Pembahasan
Berdasarkan grafik di atas diperoleh data:
| A | = | ±2 |
| T | = | 180° − 0° |
| = | 180° | |
| = | π |
Bilangan gelombangnya adalah:
Jika sudut awalnya θo = 15° maka grafiknya berbentuk sinus ke arah bawah sehingga A = −2.
| y | = | A sin k(x − θo) |
| = | −2 sin 2(x − 15°) |
Jadi, Persamaan grafik fungsi trigonometri pada gambar di atas adalah opsi (B).
Soal No. 5 tentang Persamaan Grafik Fungsi Trigonometri

A. y = cos (2x − 30°)
B. y = sin (2x + 30°)
C. y = −cos (2x − 30°)
D. y = −sin (2x − 30°)
E. y = −cos (2x + 30°)
UN 2016
Pembahasan
Grafik trigonometri pada soal di atas bisa merupakan grafik sinus maupun kosinus, tergantung fase awalnya. Perhatikan grafik berikut ini!

Pertama yang dapat kita ketahui dari grafik tersebut adalah amplitudo (A) dan periode (T).
A = ±1
T = 180° = π
Periode dapat digunakan untuk menentukan bilangan gelombang (k).
Anggap saja grafik tersebut adalah grafik sinus, maka fase awalnya θo = 30° dan amplitudonya adalah A = 1. Persamaan grafik adalah:
| y | = | A sin k(x − θo) |
| = | 1 sin 2(x − 30°) | |
| = | sin (2x − 60°) |
Ternyata persamaan ini tidak ada pada pilihan jawaban. Berarti persamaan trigonometri yang dimaksud adalah persamaan kosinus.
Fase awal persamaan kosinus pada grafik di atas adalah θo = −15° atau θo = 75°. Untuk fase awal 75° sepertinya tidak mungkin karena tidak ada opsi jawaban yang menunjukkan fase awal 75° atau kelipatannya. Jadi, sudah dapat dipastikan fase awalnya adalah −15°.
Pada fase awal −15°, grafiknya dimulai dari bawah kemudian bergerak ke atas. Hal ini berarti grafik kosinusnya adalah negatif atau amplitudonya A = −1.
| y | = | A cos k(x − θo) |
| = | −1 cos 2(x − (−15°)) | |
| = | −cos (2x + 30°) |
Jadi, persamaan grafik fungsi trigonometri berikut adalah opsi (E).
Simak juga:
Pembahasan Matematika UN: Persamaan Trigonometri
Pembahasan Matematika UN: Perbandngan Trigonometri
Pembahasan Matematika UN: Aturan Sinus dan Kosinus
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat