Rangkuman Materi, Contoh Soal & Pembahasan Bab Himpunan SMP

By Posted on

Untuk Pembelajaran selanjutnya…

Definisi Himpunan

Himpunan merupakan sekumpulan benda atau objek yang memiliki ciri-ciri sama dan dapat didefinisikan dengan jelas objek tersebut termasuk himpunan atau tidak termasuk dalam himpunan.

Istilah-istilah dalam himpunan:

  1. Anggota himpunan dilambangkan “∈”.
  2. Bukan anggota himpunan dilambangkan “∉”.
  3. Anggota himpunan ditulis di dalam “{ }”.
  4. Gunakan tanda “ , “ sebagai pemisah antara anggota yang satu dengan yang lain.
  5. Untuk jumlah anggota himpunan yang sangat banyak dan tidak dapat dituliskan satu persatu (masih berlanjut) dapat digunakan tanda tiga titik atau “ …”.
  6. Banyaknya anggota himpunan A ditulis “n(A)”.
    Beberapa cara yang digunakan untuk menyatakan himpunan, sebagai berikut:
    1. Mendaftar anggota himpunan atau Roster
      Contohnya:
      A = {Aris, Angga, Anita, Alea, Ahmad, Andi, Anti, Ana, Amara, Asti }
      B = {Bandung, Banjar, Bekasi, Bogor, Cimahi, Cirebon, Depok, Sukabumi}
    2. Menggunakan diagram Venn
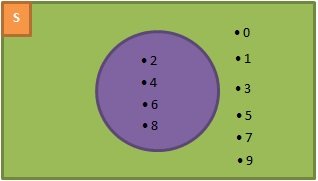
      Hal-hal yang harus diperhatikan untuk membuat diagram Venn yaitu:
      • Himpunan semesta digambarkan dengan bentuk persegi panjang dan terdapat symbol “ S “ dituliskan pada pojok kiri atas.
      • Himpunan yang menjadi fokus utama pembahasan dinyatakan dalam bentuk lingkaran atau kurva tertutup.
      • Setiap anggota himpunan dilambangkan dengan noktah atau titik yang diberi nama.
        Contohnya:
        S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
        A = {2, 4, 6, 8}
        Gambarkan diagram vennya:
    3. Menuliskan sifat anggota himpunan
      Contohnya:
      A merupakan nama-nama siswa yang memiliki huruf awal A, sedangkan B merupakan nama – nama kota di Jawa Barat. Sehingga dapat dinyatakan sebagai berikut:
      A = { Nama – nama siswa berawalan huruf A}
      B = {Nama – nama kota di Jawa Barat}
    4. Menggunakan notasi pembentuk himpunan (Rule)
      Contohnya:
      A = {x|x adalah Nama – nama siswa berawalan huruf A}
      B = {x|x Nama – nama kota di Jawa Barat}

Jenis-Jenis Himpunan

  1. Himpunan Kosong
    Himpunan kosong merupakan himpunan yang tidak memiliki anggota, dilambangkan dengan “{ }” atau “Ø”. Contohnya:
    • Himpunan bilangan asli kurang dari 1
    • Himpunan nama bulan dalam setahun yang terdiri dari 27 hari
  2. Himpunan Nol
    Himpunan nol merupakan himpunan yang hanya memiliki 0 sebagai anggota himpunannya. Contohnya:
    • Himpunan bilangan cacah yang kurang dari 1
    • Himpunan bilangan bulat antara – 1 dan 1
  3. Himpunan Semesta
    Himpunan semesta merupakan himpunan yang memuat semua anggota atau objek himpunan yang sedang dibicarakan. Himpunan ini dilambangkan dengan “ S “. Contohnya:
    A = {Aris, Angga, Anita, Alea, Ahmad}
    A adalah nama-nama siswa yang berawalan huruf AS = {Santi, Dadan, Aris, Angga, Dewi, Anita, Susan, Ahmad, Alea, Maman}
    Himpunan semesta berupa nama-nama siswa di kelas 2B
  4. Himpunan Bagian
    Himpunan bagian merupakan himpunan yang semua anggotanya terdapat di dalam himpunan lainnya. Himpunan ini dilambangkan dengan “ ⊂ “ = himpunan bagian dari. Sedangkan lambang ” ⊄ “ = bukan himpunan bagian dari. Contohnya:
    • A ⊂ B atau B ⊃ A = A adalah himpunan bagian dari B karena anggota himpunan A merupakan anggota himpunan B. A ⊄ B = A bukan himpunan bagian dari B.
    • A = {1, 3, 5, 7, 9}
      B = {1, 2, 3, 4, 5, 6,7, 8, 9, 10}
      A ⊂ B

    Banyaknya himpunan bagian dari suatu himpunan adalah 2n dengan n = banyaknya anggota himpunan tersebut. Contohnya:
    M = {1, 3, 5}
    n(M) = 3 → M = 23 = 8, yaitu { }, {1 }, {3 }, {5 }, {1,3 }, {1,5 }, {3,5}, {1,3,5 }

Hubungan Antarhimpunan

  1. Himpunan saling lepas atau saling asing
    Dua himpunan yang tidak kosong, dikatakan saling asing atau saling lepas jika himpunan tersebut  tidak memiliki anggota yang sama (anggota persekutuan). Contohnya:
    A = {1, 3, 5, 7, 9}
    B = {2, 4, 6, 8}
    A ⊃⊂ B = A dan B dua himpunan saling lepas atau saling asing karena tidak memiliki anggota yang sama.
  2. Himpunan berpotongan
    Dua himpunan yang tidak kosong dikatakan saling berpotongan bila memiliki anggota yang sama (anggota persekutuan) tetapi masih ada anggota lain pada masing-masing himpunan yang tidak sama. Himpunan yang berpotongan dilambangkan dengan “ ∩ “ dan dapat dinyatakan dengan diagram Venn.Contohnya:
    A = {a, i, u, e, o}
    B = {a, b, c, d, e, f}
    Anggota persekutuan A dan B = {a,e} sehingga A ∩ B

    Diagram Venn dari A ∩ B
  3. Himpunan sama
    Dua himpunan tidak kosong dikatakan sama apabila memiliki anggota himpunan yang sama. Contohnya:
    A = {1,2,3,4}
    B = {4,2,1,3}
    Maka A = B
  4. Himpunan ekuivalen
    Dua himpunan tidak kosong dikatakan ekuivalen jika banyak anggota dari kedua himpunan tersebut sama. Contohnya:
    A = {a,b,c,d}
    B = {1,2,3,4}
    Maka n(A) = n(B)

Operasi Himpunan

Beberapa operasi pada himpunan yaitu:

  1. Irisan himpunan (intersection/∩)
    A dan B memiliki anggota persekutuan (beririsan) → A ∩ B = {x|x ∈ A dan x ∈ B).

    Contoh:
    A = {a, i, u, e, o}
    B = {a, b, c, d, e, f}
    Anggota persekutuan A dan B = {a,e} sehingga A ∩ B

    Ketentuan yang berlaku:
    • Jika kedua himpunan sama maka akan berlaku A = B sehingga A ∩ B = A dan A ∩ B = B
    • Jika A dan B saling lepas maka A ∩ B = Ø.
    • Jika A ⊂ B maka A ∩ B = A.
  2. Gabungan himpunan (Union/∪)
    Gabungan himpunan memiliki anggota –anggota himpunan yang anggotanya berasal dari himpunan A atau himpunan B, dilambangkan dengan A ∪ B = {x|x ∈ A atau x ∈ B). Banyaknya anggota himpunan A ∪ B yaitu: n(A ∪ B) = n(A) + n(B) – n(A ∩ B).

    Contoh:
    A = {a, i, u, e, o}
    B = {a, b, c, d, e, f}
    Tentukan:
    1. A ∩ B = {a,e}, n(A ∩ B) = 2
    2. A ∪ B = {a, b, c, i, d, u, e, o, f}
    3. n(A ∪ B) = n(A) + n(B) – n(A ∩ B) = 5 + 6 – 2 = 9
      Berlaku:
      • Apabila A ∈ B maka A ∪ B = B
      • Apabila A = B maka A ∪ B = A = B
  3. Selisih himpunan (Difference/ – )
    Selisih dua himpunan meliputi semua anggota himpunan yang tidak memiliki himpunan lain. Selisih antar dua himpunan tersebut dilambangkan dengan tanda kurang ( – ), ditulis dengan persamaan A – B = {x|x ∈ A atau x ∉ B} atau B – A = {x|x ∈ B atau x ∉ A}

    Contoh:
    A = {a, b, c, d, e}
    B = {a, i, u, e, o}
    A – B = {b, c, d}
    B – A = {I, u, o}
  4. Komplemen himpunan (Ac )
    Komplemen dari sebuah himpunan A adalah himpunan semua anggota himpunan semesta (S) yang tidak ada di himpunan A. komplemen suatu himpunan dilambangkan dengan pangkat C yang melekat pada himpunan tersebut dan persamaannya AC = {x|x ∈ S tetapi x ∉ A}.

    Contoh:
    S = {1,2,3,4,5,6,7}
    A = {3,4,7}
    AC = {1,2,5,6}
  5. Beda setangkup (symmetric difference)
    Operasi himpunan beda setangkup menghasilkan anggota – anggota himpunan yang dioperasikan tetapi tidak termasuk anggota irisannya. Hasil operasi beda setangkup merupakan anggota himpunan A atau B tetapi tidak keduanya. Beda setangkup dilambangkan dengan ⊕ dan persamaannya A ⊕ B = {x|x ∈ A tetapi x ∉ B dan x ∈ B tetapi x ∉ A} atau A ⊕ B = (A∪B) – (A∩B) atau A ⊕ B = ( A – B) ∪ (B – A).

    Contoh:
    A = {a, b, c, d, e}
    B = {a, i, u, e, o}
    A ⊕ B = { b, c, d, i, u, o}

Konsep Himpunan Dalam Kehidupan Sehari-hari

Contoh:
Kelas 2B memiliki jumlah siswa 40 orang. 30 orang menyukai matematika dan 25 orang menyukai fisika. Tentukan banyak siswa yang:

  1. Gemar matematika dan fisika
  2. Gemar matematika saja
  3. Gemar fisika saja

Pembahasan:
Diketahui:
A = anggota himpunan matematika
B = anggota himpunan fisika
n(A∪B) = 40
n(A) = 30
n(B) = 25

  1. Siswa gemar matematika dan fisika = n(A∩B)
    n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
    40 = 30 + 25 – n(A ∩ B)
    40 = 55 – n(A ∩ B)
    n(A ∩ B) = 55 – 40
    n(A ∩ B) = 15
    siswa yang gemar matematika dan fisika adalah 15 siswa
  2. Siswa yang gemar matematika saja = 30 – 15 = 15 siswa
  3. Siswa yang gemar fisika saja = 25 – 15 = 10 siswa

Soal No.1

Jika diketahui A = {3, 5, 9, 12, 15} maka banyaknya himpunan bagian dari A adalah…

  1. 12
  2. 32
  3. 64
  4. 16

PEMBAHASAN :
Menentukan himpunan bagian dapat dicari menggunakan rumus : 2n
Karena jumlah anggota A (n(A)) = 5, maka himpunan bagiannya = 25= 32
Jawaban B

Soal No.2

Jika diketahui A = {bilangan ganjil di bawah 10} dan B = {bilangan prima di bawah 10} maka A ∩ B adalah….

  1. Ø
  3. {3, 5, 7, 9}
  4. {2}

PEMBAHASAN :
Anggota A = {bilangan ganjil} = {1, 3, 5, 7, 9}
Anggota B = {bilangan prima} = {2, 3, 5, 7, 9}
3, 5, 7, 9 merupakan anggota A dan B, maka
A ∩ B = {3, 5, 7, 9}
Jawaban C

Soal No.3

A = Himpunan hewan berkaki empat

B = Himpunan hewan bertanduk

A ∩ B adalah….

  1. himpunan hewan berkaki empat atau bertanduk
  2. himpunan hewan berkaki empat dan hewan bertanduk
  3. himpunan hewan berkaki empat dan himpunan hewan bertanduk
  4. himpunan hewan berkaki empat yang bertanduk

PEMBAHASAN :
A ∩ B merupakan gabungan anggota himpunan A dan anggota himpunan B. Maka:
A ∩ B = himpunan hewan berkaki empat dan hewan bertanduk
Jawaban B

Soal No.4
Yang merupakan himpunan ekuivalen adalah….

  1. A = {a, i, u, e, o}
    B = {1, 2, 3, 4, 5}
  2. A = {m, a, n, d, i}
    B = {i, d, n, a, m}
  3. A = {ayam, bebek, kelinci, sapi}
    B = {domba, jerapah, gajah, kerbau, angsa}
  4. A = {1, 2, 3 , 4, 5}
    B = {2, 4, 6, 8}

PEMBAHASAN :
Himpunan ekuivalen merupakan dua himpunan yang jumlah anggota kedua himpunan itu sama tetapi tidak sama. Yang termasuk himpunan ekuivalen adalah jawaban A karena jumlah anggotanya sama dan tidak sama
Jawaban A

Soal No.5

Jika diketahui
P = {semua jenis hewan}

Q = {semua hewan berkaki empat}

R = {semua hewan berkaki dua}

Pernyataan yang salah adalah…

  1. Q ⊂ P
  2. Q ⊂ (P ∪ Q)
  3. P ⊂ R
  4. R ⊂ P

PEMBAHASAN :
P = {semua jenis hewan}

Q = {semua hewan berkaki empat}

R = {semua hewan berkaki dua}

himpunan Q merupakan anggota himpunan P atau di tulis Q ⊂ P
himpunan R merupakan anggota himpunan P atau di tulis R ⊂ P
P ∪ Q = gabungan himpunan A dan B akan sama dengan himpunan A, atau
P ∪ Q = P, maka Q ⊂ (P ∪ Q) benar karena sama dengan Q ⊂ P
Maka jawaban yang salah adalah P ⊂ R karena seharusnya R ⊂ P
Jawaban C

Soal No.6

Jumlah siswa dari dalam satu kelas adalah 46 siswa, 25 diantaranya gemar IPA dan 21 orang gemar matematika. Jika ada 5 orang yang tidak gemar IPA dan matematika maka banyaknya anak yang gemar IPA dan matematika adalah…

  1. 8
  2. 5
  3. 6
  4. 4

PEMBAHASAN :
Diketahui:
Jumlah siswa yang gemar IPA n(A) = 25 siswa
Jumlah siswa yang gemar matematika n(B) = 21 siswa
Menentukan jumlah siswa yang gemar IPA atau matematika
n(A ∪ B) = 46 – 5 = 41 siswa
Menentukan siswa yang gemar IPA dan matematika n(A ∩ B) adalah
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
⇔ 41 = 25 + 21 – n(A ∩ B)
⇔ n(A ∩ B) = (25 + 21) – 41 = 5 siswa
Jawaban B

Soal No.7

Jika diketahui n(P) = 21 dan n(Q) = 14, n(P ∩ Q) = Ø, serta n(P ∪ Q)c = 5 maka n(Pc) adalah….

  1. 23
  2. 19
  3. 16
  4. 30

PEMBAHASAN :
Menentukan jumlah himpunan semesta n(S)
n(P ∪ Q) = n(p) + n(q) – n(P ∩ Q) = 21 + 14 – 0 = 35
maka
n(S) = n(P ∪ Q) + n(P ∪ Q)c = 35 + 5 = 40
Menentukan n(Pc) atau jumlah komplemen himpunan P (anggota himpunan semesta yang bukan anggota P)
n(Pc) = n(S) – n(P) = 40 – 21 = 19
Jawaban B

Soal No.8

Jika diketahui

S = {1, 2, 3, 4, 5, 6, 7, 8, 9}

P = {1, 3, 5, 6, 7, 9}

Q = {2, 5, 7, 8, 9}

(P ∩ Q)∪(P – Q) adalah….

PEMBAHASAN :
Menentukan (P ∩ Q)
(P ∩ Q) = {1, 3, 5, 6, 7, 9} ∩ {2, 5, 7, 8, 9} = {5, 7, 9}
Menentukan P – Q (merupakan anggota P tapi bukan anggota Q)
P – Q = {1, 3, 5, 6, 7, 9} – {2, 5, 7, 8, 9} = {1, 3, 6}
Maka (P ∩ Q)∪(P – Q)
(P ∩ Q)∪(P – Q) = {5, 7, 9} ∪ {1, 3, 6} = {1, 3, 5, 6, 7, 9} = P
Jawaban A

Soal No.9

Himpunan {1, 2, 5, 6, 15, 30} dapat dinyatakan dalam bentuk notasi yang tepat, yaitu….

  1. {x | x bilangan cacah}
  2. {x | x faktor dari 30}
  3. {x | x bilangan asli}
  4. {x | x faktor dari 44}

PEMBAHASAN 
Himpunan {1, 2, 5, 6, 15, 30} merupakan faktor dari 30, maka notasinya dapat ditulis {x | x faktor dari 30}
Jawaban B

Soal No.10

Dalam sebuah kelas terdapat 45 anak. 15 orang gemar sepak bola, 20 orang gemar bulu tangkis, dan 10 orang gemar tenis meja. Diketahui 4 anak gemar sepak bola dan bulu tangkis, 6 anak gemar bulu tangkis dan tenis meja, 5 orang gemar sepak bola dan tenis meja, serta 9 anak gemar ketiganya. Jumlah anak yang tidak gemar ketiga olahraga tersebut adalah….

  1. 1
  2. 6
  3. 4
  4. 7

PEMBAHASAN :
himpunan semesta n(S) = 45
himpunan siswa yang gemar sepak bola n(B) = 15
himpunan siswa yang gemar bulu tangkis n(T) = 20
himpunan siswa yang gemar tenis meja n(M) = 10
n(B ∩ T) = 4
n(T ∩ M) = 6
n(B ∩ M) = 5
n(B ∩ T ∩ M) = 9
Menentukan n(B ∪ T ∪ M)
n(B ∪ T ∪ M) = n(B) + n(T) + n(M) – n(B ∩ T) – n(T ∩ M) – n(B ∩ M) + n(B ∩ T ∩ M) = 15 + 20 + 10 – 4 – 6 – 5 + 9 = 39
Menentukan siswa yang tidak menyukai ketiga olahraga tersebut
n(S) – n(B ∪ T ∪ M) = 45 – 39 = 6 orang
Jawaban B

Soal No.11

Himpunan bilangan asli berikut ini adalah …

  1. {…, -2, -1, 0, 1, 2, …}
  2. {0, 1, 2, 3, 4, 5, …}
  3. {- ½ , ½ , – ¼ , ¼ }
  4. {1 ,2 ,3, 4, 5, …}

PEMBAHASAN :
Beberapa anggota himpunan berikut:

  • {…, -2, -1, 0, 1, 2, …} → himpunan bilangan bulat
  • {0, 1, 2, 3, 4, 5, …} → himpunan bilangan cacah
  • {- ½ , ½ , – ¼ , ¼ } → himpunan bilangan pecahan
  • {1 ,2 ,3, 4, 5, …} → himpunan bilangan asli

Jawaban D

Soal No.12

Diketahui {faktor 36} ditulis dengan mendaftar anggotanya maka yang benar adalah …

  1. {1,2,3,4,6,9,12,18,36}
  2. {2,3,4,6,7,9,12,18,20,36}
  3. {1,2,3,4,5,6,9,12,15,18}
  4. {2,4,6,9,12,18,36}

PEMBAHASAN :
Untuk menentukan faktor dari 36, dapat dicari dengan menghitung perkalian yang menghasilkan angka 36 sebagai berikut:
1 x 36
2 x 18
3 x 12
4 x 9
6 x 6
Sehingga himpunan untuk faktor 36 = {1,2,3,4,6,9,12,18,36}
Jawaban A

Soal No.13

Jenis himpunan di bawah ini adalah himpunan nol, yaitu …

  1. Himpunan bilangan asli kurang dari 10
  2. Himpunan bilangan cacah kurang dari 1
  3. Himpunan bilangan prima kurang dari 6
  4. Himpunan bilangan asli kurang dari 1

PEMBAHASAN :

  • Himpunan bilangan asli kurang dari 10
    ⇔ {1,2,3,4,5,6,7,8,9}
  • Himpunan bilangan cacah kurang dari 1
    ⇔ {0}
  • Himpunan bilangan prima kurang dari 6
    ⇔ {2,3,5}
  • Himpunan bilangan asli kurang dari 1
    ⇔ tidak ada bilangan asli kurang dari 1

Jawaban B

Soal No.14

Berikut ini pernyataan yang benar adalah …

  1. A ⊂ B atau B ⊃ A
  2. 4 ⊂ {bilangan genap}
  3. {bilangan cacah} ⊂ {bilangan asli}
  4. -2 ∈ {bilangan cacah}

PEMBAHASAN :

  • A ⊂ B atau B ⊃ A (benar)
    A adalah himpunan bagian dari B karena anggota himpunan A merupakan anggota himpunan B
  • 4 ⊂ {bilangan genap} (salah)
    Seharusnya 2 ∈ { bilangan genap}
  • {bilangan cacah} ⊂ {bilangan asli} (salah)
    Seharusnya {bilangan cacah} ⊂ {bilangan bulat}
  • -2 ∈ {bilangan cacah} (salah)
    Seharusnya -2 ∈ {bilangan bulat}

Jawaban A

Soal No.15

Di bawah ini yang bukan merupakan himpunan bagian dari P ={a,i,u,e,o} adalah …

  1. {a,u}
  2. {u,o}
  3. {a,c}
  4. {i,e}

PEMBAHASAN :
{a,u} ∈ {a,i,u,e,o}
{u,o} ∈ {a,i,u,e,o}
{a,c} → c ∉ {a,i,u,e,o}
{i,e} ∈ {a,i,u,e,o}
Jawaban C

Soal No.16

Diketahui himpunan sebagai berikut:

A = {1,2,3,4,5}
B = {K,L,M,N,O}
Kedua himpunan di atas memiliki hubungan sebagai berikut …

  1. A = B
  2. A ⊂ B
  3. B ⊂ A
  4. A ⊃⊂ B

PEMBAHASAN :

  • A = B = Dua himpunan tidak kosong dikatakan sama apabila memiliki anggota himpunan yang sama
  • A ⊂ B = A adalah himpunan bagian dari B karena anggota himpunan A merupakan anggota himpunan B
  • B ⊂ A = B adalah himpunan bagian dari A karena anggota himpunan B merupakan anggota himpunan A
  • A ⊃⊂ B = A dan B dua himpunan saling lepas atau saling asing karena tidak memiliki anggota yang sama.

Jawaban D

Soal No.17

Berikut ini beberapa himpunan, yaitu:

A = {bilangan asli kurang dari 8}

B = {bilangan ganjil kurang dari 15}

C = {bilangan pada sebuah dadu}

D = {x | 0 < x < 8, x bilangan bulat}

Pernyataan yang sesuai dengan anggota himpunan di atas adalah …

  1. A = C
  2. A = B
  3. B = D
  4. B = C

PEMBAHASAN :
A = {bilangan asli kurang dari 10}
⇔ {1,2,3,4,5,6,7,8,9} → n(A) = 9

B = {bilangan ganjil kurang dari 15}
⇔ {1,3,5,7,9,11,13} → n(B) = 7

C = {bilangan pada sebuah dadu}
⇔ {1,2,3,4,5,6} → n(C) = 6

D = {x | 0 < x < 8, x bilangan bulat}
⇔ {1,2,3,4,5,6,7} → n(D) = 7
Jawaban C

Soal No.18

Anggota himpunan A = {a,b,c,d,e} dengan himpunan semesta (S) = {a,b,c,d,e,f,g,h,i}. komplemen himpunan dari A adalah …

  1. {f,g,h,i}
  2. {0}
  3. {b,c,d,f,g,h}
  4. {a,e,i}

PEMBAHASAN :
Komplemen himpunan (Ac ) merupakan komplemen dari sebuah himpunan A adalah himpunan semua anggota himpunan semesta (S) yang tidak ada di himpunan A.
A = {a,b,c,d,e}
(S) = {a,b,c,d,e,f,g,h,i}
Ac = {f,g,h,i}
Jawaban A

Soal No.19

Terdapat himpunan  A = {faktor dari 24} dan B = {faktor dari 32}. Jumlah himpunan A dan B adalah …

  1. {1,2,3,4,6,8,12,24}
  2. {1,2,4,8}
  3. {2,4,6,8,12,16,24,32}
  4. {1,2,3,4,6,8,12,16,24,32}

PEMBAHASAN :
Untuk menentukan faktor dari suatu bilangan, dapat dicari dengan menghitung perkalian yang menghasilkan angka tersebut sebagai berikut:

Faktor dari 24:
1 x 24
2 x 12
3 x 8
4 x 6
A = {1,2,3,4,6,8,12,24}

Faktor dari 32:
1 x 32
2 x 16
4 x 8
B = {1,2,4,8,16,32}

Maka A + B  = {1,2,3,4,6,8,12,24} + {1,2,4,8,16,32} = {1,2,3,4,6,8,12,16,24,32}
Jawaban D

Soal No.20

Diketahui n(A∪B) = 30, n(A) = 15, n(B) = 20, maka n(A∩B) adalah …

  1. 1
  2. 5
  3. -2
  4. -3

PEMBAHASAN :
n(A∪B) = 30
n(A) = 15
n(B) = 20

maka:
n(A∪B) = n(A) + n(B) – n(A∩B)
30 = 15 + 20 – n(A∩B)
n(A∩B) = 35 – 30
n(A∩B) = 5
Jawaban B

Soal No.21

Apabila A = {x| -4 < x -1 < 0, x Î himpunan bilangan bulat}. Banyaknya himpunan bagian dari A adalah …

  1. 32
  2. 20
  3. 16
  4. 8

PEMBAHASAN :
Menyelesaikan pertidaksamaan sebagai berikut:
-4 < x -1 < 0
⇔ -4 + 1 < x -1 + 1 < 0 + 1
⇔ -3 < x < 1
Diperoleh A = {-2, -1, 0} → n(A) = 3

Maka banyaknya himpunan bagian dari A = 2n = 23 = 8
Jawaban D

Soal No.22

Diketahui berikut ini adalah himpunan dari semesta pembicaraan  {1,3,5}, kecuali …

  1. Himpunan bilangan asli
  2. Himpunan bilangan ganjil
  3. Himpunan bilangan cacah
  4. Himpunan bilangan prima

PEMBAHASAN :

  • Himpunan bilangan asli = {1,2,3,4,5, …} → {1,3,5} ⊂ {1,2,3,4,5, …}
  • Himpunan bilangan ganjil = {1,3,5,7,9, …} → {1,3,5} ⊂ {1,3,5,7,9, …}
  • Himpunan bilangan cacah = {0,1,2,3,4,5, …} → {1,3,5} ⊂ {0,1,2,3,4,5, …}
  • Himpunan bilangan prima = {2,3,5,7, …} → {1,3,5} ⊄ {2,3,5,7, …}

Jawaban D

Soal No.23

Diketahui suatu himpunan {1,2,3}, banyak himpunan bagian dengan jumlah anggota = 2 adalah …

  1. 2
  2. 3
  3. 4
  4. 5

PEMBAHASAN :
Himpunan {1,2,3} → n = 3
Sehingga himpunan bagian dari himpunan tersebut = 2n = 23 = 8, yaitu { }, {1}, {2}, {3}, {1,2}, {1,3 }, {2,3}, {1,2,3}

Maka, banyak himpunan bagian yang memiliki 2 anggota adalah 3
Jawaban B

Soal No.24

Diketahui A ⊂ B, perhatikan beberapa pernyataan di bawah ini:

  1. A ∪ B = A
  2. B ⊂ A
  3. A ∩ B = A
  4. A ∪ B = B

Pernyataan yang benar adalah …

  1. 1 dan 4
  2. 2 dan 3
  3. 3 dan 4
  4. 1 dan 3

PEMBAHASAN :
A ⊂ B, A adalah himpunan bagian dari B karena anggota himpunan A merupakan anggota himpunan B. Maka dapat disimpulkan bahwa:

  1. A ∪ B = Ø → Gabungan himpunan memiliki anggota –anggota himpunan yang anggotanya berasal dari himpunan A atau himpunan B, bukan himpunan kosong.
  2. B ⊂ A ≠ A ⊂ B
  3. A ∩ B = A → Jika A ⊂ B maka A ∩ B = A
  4. A ∪ B = B → Jika A ⊂ B maka A ∪ B = B

Jawaban C

Gambar untuk no 25 – 27 perhatikan gambar di bawah ini!

Soal No.25

P ∩ Q = …

  1. {1,3 }
  2. {1,2,3,6,9}
  3. {2,6,9}
  4. { }

PEMBAHASAN :
P = {1,2,3,6}
Q = {1,3,9}
Maka P ∩ Q = {1,3}
Jawaban A

Soal No.26

(P – Q)C = …

  1. {1,3,4,5,7,8,9}
  2. {2,6}
  3. {1,2,3,6}
  4. {1,3,9}

PEMBAHASAN :
P – Q = {1,2,3,6} – {1,3,9} = {2,6}
(P – Q)C = {1,3,4,5,7,8,9}
Jawaban A

Soal No.27

(P ∩ Q) ∪ P = …

  1. {1,3}
  2. {2,6}
  3. {1,2,3,6}
  4. { }

PEMBAHASAN :
P ∩ Q = {1,3}
P = {1,2,3,6}
Maka, (P ∩ Q) ∪ P = {1,3} ∪ {1,2,3,6} = {1,2,3,6}
Jawaban C

Soal No.28

Jika M ⊂ N dan N ⊂ M dengan anggota M = 10. Maka n (M ∩ N) adalah …

  2. 1
  3. 10
  4. 20

PEMBAHASAN :
M ⊂ N dan N ⊂ M → M = N maka (M ∩ N) = M = N
Sehingga n (M ∩ N) = n(M) = n(N) = 10
Jawaban C

Soal No.29

Jika A = {x|x ≥ 6, x ∈ bilangan asli} dan B = {x|x ≤ 10, x ∈ bilangan prima}. Maka A ∩ B adalah …

  1. {7}
  2. {2,3,5,7}
  3. { }
  4. {6,7,8}

PEMBAHASAN :
Menentukan anggota himpunan A:
A = {6,7,8,9,10, …}

Menentukan anggota himpunan B:
B = {2,3,5,7}
Maka A ∩ B = {7}
Jawaban A

Soal No.30

Jika P = {1,2,3,4,5} dan Q = {a,i,u,e,o}. Pernyataan yang tepat adalah …

  1. P ⊂ Q
  2. Q ∈ P
  3. P ∪ Q = {0}
  4. P ∼ Q

PEMBAHASAN :

  • P ⊂ Q → P bukan himpunan bagian dari Q
  • Q ∈ P → Q bukan anggota himpunan P
  • P ∪ Q = {0} → P ∪ Q = {1,a,2,i,3,u,e,4,o,5}
  • P ~ Q
    P = {1,2,3,4,5} → n(P) = 5
    Q = {a,i,u,e,o} → n(Q) = 5
    n(P) = n(Q) maka P ~ Q

Jawaban D

Soal No.31

Jumlah siswa di kelas 2B berjumlah 35 orang. Jika 20 orang siswa menggemari pelajaran menggambar dan 25 orang siswa menggemari pelajaran IPA. Maka jumlah siswa yang hanya menggemari pelajaran IPA saja adalah …

  1. 15
  2. 16
  3. 17
  4. 18

PEMBAHASAN :
Diketahui:
A = siswa penggemar menggambar
B = siswa penggemar IPA
n(A ∪ B) = 35
n(A) = 20
n(B) = 25

Rumus yang berlaku:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
35 = 20 + 25 – n(A ∩ B)
35 = 45 – n(A ∩ B)
n(A ∩ B) = 10 → siswa yang menggemari pelajaran menggambar dan IPA

Maka jumlah siswa yang hanya menggemari  IPA = 25 – 10 = 15 orang
Jawaban A

Soal No.32

Jumlah siswa di kelas 3A adalah 45 orang. Beberapa orang siswa mengikuti kegiatan ekstrakurikuler sebagai berikut: 20 siswa mengikuti basket, 30 orang mengikut badminton, dan 10 orang tidak mengikuti keduanya. Maka selisih siswa yang hanya mengikuti kegiatan basket saja dan badminton saja adalah … orang.

  1. 10
  2. 12
  3. 15
  4. 17

PEMBAHASAN :
Diketahui:
A = basket
B = badminton
n(S) = 45
n(A ∪ B)C = 10
n(A) = 20
n(B) = 30

sehingga:
n(A ∪ B) = n(S) – n(A ∪ B)C
n(A ∪ B) = 45 – 10
n(A ∪ B) = 35

diperoleh:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
35 = 20 + 30 – n(A ∩ B)
n(A ∩ B) = 50 – 35
n(A ∩ B) = 15

Jumlah siswa yang mengikuti basket saja = 20 – 15 = 5 orang
Jumlah siswa yang mengikuti badminton = 30 – 15 = 15 orang
Maka selisih nya adalah 15 – 5 = 10 orang
Jawaban A

Soal No.33

Perhatikan gambar di bawah ini!

Diagram venn pada gambar di atas adalah …

  1. A ∩ B
  2. A – B
  3. A ∪ B
  4. A ⊕ B

PEMBAHASAN :

  • A ∩ B
  • A – B
  • A ∪ B
  • A ⊕ B

Jawaban D

Soal No.34

Pernyataan yang tepat untuk A ⊃⊂ B adalah …

  1. A ∼ B
  2. A ∪ B = B
  3. A ∩ B = Ø
  4. A = B

PEMBAHASAN :
A ⊃⊂ B = A dan B dua himpunan saling lepas atau saling asing karena tidak memiliki anggota yang sama. Maka pilihan yang tepat di cek setiap pilihan jawaban:

  1. A ~ B → jumlah anggota himpunan A dan anggota himpunan B sama, himpunan tidak saling lepas/ asing
  2. A ∪ B = B → A ∈ B, himpunan tidak saling lepas
  3. A ∩ B = Ø → himpunan yang tidak memiliki anggota irisan, himpunan saling lepas
  4. A = B → memiliki anggota himpunan yang sama, himpunan tidak saling lepas

Maka jawaban yang tepat adalah C
Jawaban C

Soal No.35

Perhatikan diagram venn di bawah ini!

Daerah yang diarsir merupakan daerah …

  1. A ∩ B
  2. A – B
  3. AC
  4. B – A

PEMBAHASAN :
Maka pilihan yang tepat di cek setiap pilihan jawaban:

  1. A ∩ B
  2. A – B
  3. AC
  4. B – A

Maka jawaban yang tepat adalah D
Jawaban D

Soal No.36

Diketahui:

P = {x|x ∈ faktor dari 18}

Q = {x|x ∈ faktor dari 20}

Sehingga banyaknya himpunan bagian dari P ∩ Q adalah …

  1. 4
  2. 16
  3. 32
  4. 64

PEMBAHASAN :
Menentukan anggota himpunan P:
P = {x|x ∈ faktor dari 18}
1 x 18
2 x 9
3 x 6
P = {1,2,3,6,9,18}

Menentukan anggota himpunan Q:
1 x 20
2 x 10
4 x 5
Q = {1,2,4,5,10,20}
P ∩ Q = {1,2} → n(P ∩ Q) = 2
Maka banyak himpunan bagian dari P ∩ Q = 2n = 22 = 4
Jawaban A

Soal No.37

Diketahui:

S = {1,2,3,4,5,6,7,8,9,10}

P = {2,3,5,7}

Q = {2,4,6,8,10}

Maka (P ∪ Q)C adalah …

  1. { }
  2. {1,2,3,4,5,6,7,8,9,10}
  3. {1,9}
  4. {2,3,5,7}

PEMBAHASAN :
P = {2,3,5,7}
Q = {2,4,6,8,10}
P ∪ Q = {2,3,4,5,6,7,8,10}
Maka (P ∪ Q)C = {1,9}
Jawaban C

Soal No.38

Diketahui dari 40 orang karyawan suatu pabrik, sebanyak 25 orang hobi minum kopi, 20 orang hobi minum teh, dan 10 orang hobi minum keduanya. Maka jumlah karyawan yang tidak menyukai kopi dan teh adalah …

  1. 1
  2. 5
  3. 10
  4. 15

PEMBAHASAN :
Diketahui:
Jumlah himpunan semesta = n(S) = 40
Himpunan peminum kopi = n(A) = 25
Himpunan peminum teh = n(B) = 20
Himpunan peminum keduanya = n(A ∩ B) = 10

Sehingga:
n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
n(A ∪ B) = 25 + 20 – 10
n(A ∪ B) = 35
Maka jumlah karyawan yang tidak menyukai kopi dan teh = 40 – 35 = 5 orang
Jawaban B

Soal No.39

Diketahui P ⊂ Q , jika n(P) = 10 dan n(Q) = 10. Pernyataan yang tepat,kecuali …

  1. Q ⊂ P
  2. P ~ Q
  3. n(P ∩ Q) = 0
  4. P = Q

PEMBAHASAN :
Cek tiap pilihan jawaban:

  1. Q ⊂ P = P ⊂ Q, karena n(P) = n(Q)
  2. P ~ Q karena n(P) = n(Q)
  3. n(P ∩ Q) ≠ 0 → n(P ∩ Q) = 10
  4. P = Q karena n(P) = n(Q)

Maka jawaban yang kurang tepat adalah C
Jawaban C

Soal No.40

Banyaknya himpunan bagian dari {huruf pembentuk kata “prisma”} adalah …

  1. 64
  2. 32
  3. 16
  4. 8

PEMBAHASAN :
{huruf pembentuk kata “prisma”} = {p,r,i,s,m,a} = n = 6
Maka banyak himpunan bagian tersebut = 2n = 26 = 64
Jawaban A

Semoga Bermanfaat

Related posts:

Artkel Terkait  Pembahasan Fisika UN 2018 No. 26

Leave a Reply

Your email address will not be published. Required fields are marked *