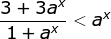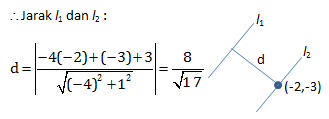Untuk Pembelajaran selanjutnya…
Soal No.1
Jika 0 < a < 1, maka
mempunyai penyelesaian…
- x > loga 3
- x < -2 loga 3
- x < loga 3
- x > -loga 3
- x < 2 loga 3
PEMBAHASAN :
⇒ 3 < ax
⇒ ax > 3
Karena 0 < a < 1
⇒ alog(ax) < alog(3)
⇒ x.alog a < alog 3
⇒ x. 1 < alog 3
⇒ x < loga 3
Jawaban C
DOWNLOAD SOAL UTBK MATEMATIKA TAHUN 2019 & PEMBAHASANNYA PART I DALAM BENTUK PDF KLIK DISINI
Soal No.2
Lingkaran yang berpusat di (a,b), dengan a,b > 3, menyinggung garis 3x + 4y = 12. Jika lingkaran tersebut berjari-jari 12, maka 3a + 4b =….
- 24
- 36
- 48
- 60
- 72
PEMBAHASAN :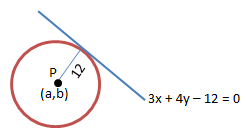
a > 3, b > 3
Jarak P(a,b) ke garis 3x + 4y – 12 = 0 adalah 12 (r = 12)
⇒
⇒60 = |3a + 4b – 12|
⇒(3a + 4b – 12 + 60).(3a + 4b -12 – 60) = 0
⇒(3a + 4b + 48).(3a + 4b – 72) = 0
⇒ 3a + 4b = 72
Jawaban E
LIHAT JUGA : Soal UTBK I Matematika 2019 Part II
Soal No.3
Jumlah semua ordinat penyelesaian sistem persamaan
adalah…
- -2
- 1
- 2
- 4
PEMBAHASAN :
Jawaban A
Himpunan penyelesaian dari |x – 1|
adalah interval (a,b). Nilai 3a + 2b adalah….- 2
- 4
- 6
- 12
PEMBAHASAN :
∴ Gabungannya 1 ≤ x ≤ 3 ∪ 0 < x < 1
⇒ 0 < x < 3
⇒ (0,3) ≡ (a,b)
⇒ a = 0, b = 3
∴ 3a + 2b = 3.0 + 2.3 = 6
Jawaban D
Soal No.5
Jika p(x) = ax3 + bx2 + 2x – 3 habis dibagi x2 + 1, maka nilai 3a – b adalah…
PEMBAHASAN :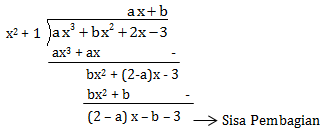
Karena habis dibagi, berarti sisa pembagiannya nol:
(2 – a)x – b – 3 = 0
⇒ 2 – a = 0 dan -b – 3 = 0
⇒ a = 2 dan b = -3
∴ 3a – b = 3.(2) – (-3) = 6+3 = 9
Jawaban D
Soal No.6
Jika diketahui suku barisan aritmatika bersifat xk+2 = xk+p, dengan p ≠ 0, untuk sebarang bilangan asli positif k, maka x3 + x5 + x7 + ….. +x2n+1 =…
PEMBAHASAN :
xk+2 = xk + P
x3 = x1 + p
Pada barisan xn : x1, x2, x3,….
bedanya adalah:
2b* = x3 – x1
⇒ 2b* = (x1 + p) – x1
⇒ b* = 
Pada barisan x2n+1 : x3, x5, x7,…
bedanya adalah : b = p
suku pertamanya : U1 = a = x3 = x2 + 
Jawaban A
Soal No.7
- 2K(|a| – 1)2
- K(|a| – 1)2
- 4aK(|a| – 1)2
- aK(|a| – 1)2
- K2(|a+K| – 1)2
PEMBAHASAN :
= K.[(|a|-1)2 + (|a|-1)2.[a+a]
= K. [2.(|a|-1)2].2a
= 4aK(|a| – 1)2
Jawaban C
Soal No.8
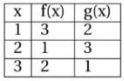
Diketahui grafik fungsi f’ dan g’ dengan beberapa nilai fungsi f dan g sebagai berikut
Jika h(x) = (fog)(x), maka nilai h'(2) adalah…
PEMBAHASAN :
h(x) = (fog)(x) = f(g(x))
h'(x) = g'(x).f'(g(x))
h'(2) = g'(2).f'(g(2))
Dengan melihat tabel fungsi f(x), g(x) serta kurva f'(x), g'(x), didapat:
g(2) = 3, g'(2) = 3, f'(3) = -3
Maka:
h'(2) = 3. f'(3) = 3. (-3) = -9
Jawaban B
Diberikan fungsi f dengan sifat f(x+3) =f(x) untuk tiap x. Jika
….- -4
- -6
- -8
- -10
- -12
PEMBAHASAN :
Jawaban A
Soal No.10
Misalkan l1 menyatakan garis singgung kurva y = x2 + 1 di titik (2,5) dan I2 menyatakan garis singgung kurva y = 1 – x2 yang sejajar dengan garis l1. Jarak l1 dan l2 adalah….
PEMBAHASAN :
Garis singgung 1, di (2,5) :
- Gradien l1 : m1 = y1‘ = (x2 + 1)’ = 2x = 2.(2) = 4
- l1 : y – 5 = 4(x-2)
⇒ y = 4x – 3
⇒ -4x + y + 3 = 0
Garis singgung 2
- Gradien l2 : m2 = m1 (karena l1 // l2)
⇒ m2 = 4
⇒ (1 – x2 = 4
⇒ -2x = 4
⇒ x = -2, y = 1 – (-2)2 = -3
Jawaban D
DOWNLOAD SOAL UTBK MATEMATIKA TAHUN 2019 & PEMBAHASANNYA PART I DALAM BENTUK PDF KLIK DISINI
Semoga Bermanfaat