Soal dan Pembahasan VEKTOR fisika | 25+ soal

 25 + soal dan pembahasan vektor fisika SMA  MA SMK kelas 10 

[update soal terbaru 2020]

soal vektor 1
1. Kelompok besaran di bawah ini yang termasuk besaran vektor adalah . . . .
a. kelajuan, kuat arus, gaya
b. energi, usaha, banyak mol zat
c. kecepatan, momentum, kuat arus listrik
d. tegangan, intensitas cahaya, gaya
e. gaya, percepatan, waktu
jawab: C
pembahasan:
besaran vektor adalah besaran yang memiliki nilai dan arah

soal vektor 2
2. Besaran-besaran berikut yang dipengaruhi arahnya adalah ….
a. massa           d. jarak
b. waktu           e. kecepatan
c. usaha
jawab: E
kecepatan adalah besaran vektor

soal 3 tentang melukis vektor
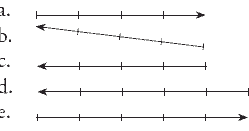
3. Seseorang menarik meja ke arah barat dengan gaya 60 N. Jika 1 cm mewakili gaya 15 N, gambar vektor gaya tersebut yang benar adalah . .
gambar  no 3

jawab: C
pembahasan:
dalam peta barat ditunujukkan dengan arah kekiri dan memiliki skala 60 : 15 = 4 cm

#soal 4 tentang resultan vektor segaris saling berlawanan
4. Pada perlombaan tarik tambang, kelompok A menarik ke arah timur dengan gaya 700 N. Kelompok B menarik ke barat dengan gaya 665 N. Kelompok yang memenangi perlombaan adalah kelompok . . . .
a. A dengan resultan gaya 25 N
b. A dengan resultan gaya 35 N
c. B dengan resultan gaya 25 N
d. B dengan resultan gaya 35 N
e. B dengan resultan gaya 45 N
jawab:  B
pembahasan:
jika kedua vektor saling berlawanan maka dikurang
R = A – B
R = 700 – 665
R = 35 N manang A 

Perhatikan gambar vektor- vektor berikut untuk menjawab 3 soal tentang menggambar vektor dengan metode poligon berikut

#soal 5 menggambar resultan vektor dengan metode jajar genjang

5. Gambar resultan dari a + b dengan metode jajargenjang yang benar adalah. . . .

jawab: D
pembahasan pada jawaban D kedua kaki a dan b berimpit

#soal  6
6. Gambar resultan dari a − c − d dengan metode poligon yang benar adalah . . . .

#soal 8 tentang komponen vektor pada sumbu x dan y
8. Sebuah mobil bergerak dengan kecepatan 50 km/jam membentuk sudut 30° terhadap sumbu x positif. Besar komponen vektor kecepatan tersebut pada sumbu x dan sumbu y berturut-turut adalah . . . .
a. 25 km/jam dan 25 √2 km/jam
b. 25 km/jam dan 25 √3 km/jam
c. 25 √3 km/jam dan 25 km/jam
d. 25 √3 km/jam dan 25 √2 km/jam
e. 25 √3 km/jam dan 25 √3 km/jam
jawab: C

jawab: E



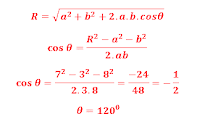
#soal  12
12.  Jika sebuah vektor kecepatan v = 10 m/s diuraikan menjadi dua buah vektor yang saling tegak lurus dan salah satu vektor uraiannya membentuk sudut 60° dengan sumbu x, maka besar masing-masing vektor uraiannya berturut-turut pad sumbu x dan y  adalah …
a. 5 m/s dan 5 √3 m/s   
b. 5 m/s dan 5 √2 m/s   
c. 10 m/s dan 10 √3 m/s

d. 5 m/s dan 5 √6 m/s

e. 10 m/s dan 1 m/s
jawab: A
v_x = v.cos 60 = 10. ½  = 5
vy = v sin 60 = 50 . ½ √3 = 5 √3

#soal 13
13.  Perhatikan diagram vektor berikut ini!

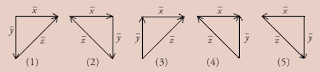
Yang menyatakan adanya hubungan x = y – z adalah gambar … .
a. (1)     

b. (2)       

c. (3)     

d. (4) 

e. (5)
jawab:  E
pembahasan:
dengan menggabar poligon dapat ditentukan jawaban yang benar
gambar (1) : y + z = x
gambar (2) : x + y = z
gambar (3) : y + x = z
gambar (4) :  z + x = y
gambar (5) : x + z = y atau x = y- z

#soal  14 tentang resulton vektor perahu dan aliran sungai
14.  Perahu saat digunakan diaair yang tenang mampu bergerak dengan kecepatan 1,2 m/s . Jika berada di sungai yang memiliki kecepatan arus air sebesar 0,5 m/s dan perahu bergerak searah arus sungai, maka resultan vektor kecepatan perahu sekarang sebesar ….
a. 0,6 m/s          d. 1,7 m/s
b. 0,7 m/s          e. 2,4 m/s
c. 1,3 m/s
jawab: D (R = 1,2+0,5 = 1,7 m/s)

#soal  15
15.  Vektor a = 3 satuan, vektor b = 4 satuan dan a + b = 5 satuan, besar sudut yang diapit oleh vektor a dan b adalah ….
a. 90^O                d. 120 ⁰
b. 45 ^O                e. 180 ⁰
c. 60 ^O
Jawab: A

pembahasan:
3 , 4 dan 5 adalah triple phytagoras pada segitiga siku siku (segitiga dengan sudut 90)

#soal 16
16. Seseorang ingin menyeberangi sungai deras dengan perahu yang mampu bergerak dengan kecepatan 2 m/s. Kecepatan arus sungai 1,2 m/s. Supaya orang tersebut dapat menyeberang sungai secara tegak lurus arus sungai maka perahunya harus diarahkan dengan sudut α terhadap arus sungai. Besar α adalah ….
a. 37^O                d. 127^O
b. 53 ^O                e. 143^O
c. 90 ^O
jawab: D
pembahasan:


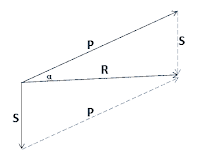
sin α = s/p = 1,2/2 = 0,6

α = 37

θ = 127

#soal 17
17.  Sebuah balok ditarik tiga gaya seperti pada gambar. Resultan gaya yang bekerja pada balok sebesar ….

a. 2 N

b. 6 N

Artkel Terkait  Pembahasan Biologi No. 46 - 50 TKD Saintek SBMPTN 2017 Kode Naskah 157

c. 10 N

d. 14 N

e. 22 N

jawab: C (triple phytagoras)

komponen x 

X = 10 – 4 = 6

y = 8

R² = x² + y²

R² =6² + 8²

R² = 36 + 64 = 100

R = √100 = 10 N

#soal 18 tentang selisih vektor yang membentuk sudut
18.  Dua buah gaya sama besar yaitu 10 N membentuk sudut 120^O satu sama lain. Selisih kedua vektor tersebut adalah….

a. 0 N                 d. 10√3 N

b. 10 N               e. 20 N

c. 10√2 N

#soal 19
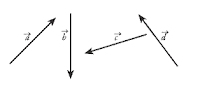
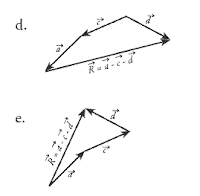
19.  Gambar manakah dari vektor berikut yang memenuhi persamaan a + b + c= 0 ?

#soal 20
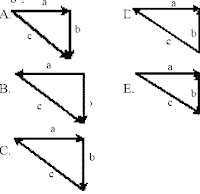
20.  Perhatikan gambar. Proyeksi vektor pada arah vertikal dan horisontal sebesar …

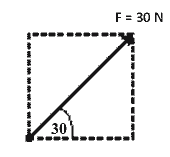
a. 15 N dan 15√3 N
b. 15√3 N dan 15 N
c. 15√2 N dan 15√2 N
d. 30 N dan 30√3 N
e. 30√3 N dan 30 N
jawab: B

F_y = F sin 30 = 30 . ½ √ = 15

#soal 21
21.  Sebuah balok cukup berat berada di atas lantai mendatar licin ditarik gaya seperti pada gambar. tg 37^o = 0,75. Komponen gaya yang searah gerak benda tersebut adalah ….

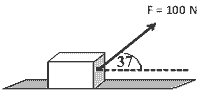
a. 50√3 N
b. 80 N
c. 75 N
d. 60 N
e. 50 N
jawab; B

fx = f. cosθ = 100.0,8 = 80 N

#soal  22
22. Perhatikan vektor-vektor yang besar dan arahnya terlukis pada kertas berpetak seperti gambar di samping. Jika panjang satu petak adalah dua newton (N), maka besar resultan kedua vektor adalah ….

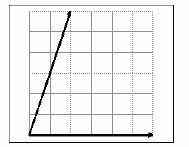
a. 16 N               d. 22 N
b. 18 N               e. 24 N
c. 20 N

R = 20 (triple phytagoras)

#soal  23
23. Perhatikan gambar gaya-gaya di bawah ini! Besar resultan ketiga gaya tersebut adalah…

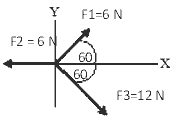
a. 4,0 N
b. 4√3 N
c. 6,0 N
d. 6 √3 N
e. 8 N

jawab: C
mencari besar resultan gaya

komponen vektor pada sumbu x
F1x = F1 . cos 60 = 6 . 1/2 = 3
F2x = – 6
F2x = F2 . cos 60 = 12 . 1/2 = 6
ΣFx = 3 – 6 + 6 = 3

komponen vektor pada sumbu y:
F1y = F1 . sin 60 = 6 . 1/2(√3) = 3
F2y = 0
F3y = – F3 . sin 60 = – 12 .1/2 (√3)
ΣFy = 3(√3) + 0 – 6(√3) = -3(√3)

rumus besar resultan:

R² = ΣFx² + ΣFy²
R² = 3² + (-3√3)²
R² = 9 + 27
R² = 36
R = √36 = 6 N

#soal 24
24.  Dua vektor a dan b memiliki nilai titik tangkap yang sama dan nilai yang sama pula. Jika sudut apit antara kedua vektor adalah β , maka berlaku hubungan:

|a+b| = 2|a-b|

maka cos β adalah ….
(A) ½
(B) 1/3
(C) 1/6
(D) 1/4
(E) 1/5
Jawab: B

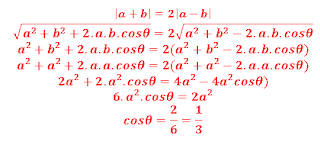
#soal 25
25.  F ₁ ,F ₂ , dan F ₃ adalah tiga buah vektor gaya yang menghasilkan resultan nol seperti pada gambar

(E) 150 newton dan 50 newton

jawab:
pembahasan:

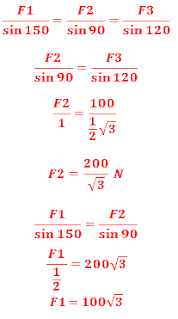
26. perhatikan gambar berikut!

besar resultan ketiga vektor diatas adalah… N

Artkel Terkait  Pembahasan Kimia No. 56 - 60 TKA Saintek UTBK SBMPTN 2019

a. 5

b. 5√3 

c. 10

d. 10 √3

e. √3

pembahasan 

pembahasan soal vektor analisis dan komponen”>

F1 = 20N

Sudut = 60 terhadap sumbu y positif

F1x = 20 . sin 60 = 20 . ½ √3 = 10√3

F1y = 20 . cos 60 = 20 . ½  = 10

 

F2 =10 N

Sudut = 30 terhadap sumbu x negatif

F2x = -10 . cos 30 = – 10 . ½ √3  = – 5√3

F2y = 10 . sin 30 = 10 . ½ = 5

 

F3 = 30 N

F3x = 0

F3y = -30

 

Resultan

ΣFx = 10√3 – 5√3 = 5√3

ΣFy = 10 + 5 –
30 = -15

R² = ΣFx² + ΣFy²

R² = 5√3² + (-15)²

R² = 75 + 225

R² = 300

R = 10√3

soal perkalian vektor

27. Dua buah vektor A dan B masing – masing
A = (2i + j – k)
B = (i +3j + k)
hitung besar dari:
a. A . B
b. A x B
Penyelesaian / pembahasan:
Dari soal kita lakukan perkalikan seperti biasa:

(2i + j – k)(i +3j + k)

a. perkalian dot product vektor antara A dan B

(2i + j – k) . (i +3j + k)

A . B = 2i.i + 2i.3j + 2i.k + j.i + j.3j + j.k – k.i – k.3j – k.k 

A . B = 2+ 0 + 0 + 0 + 3 +0 – 0 – 0 – 1 = 2 + 3 – 1 = 4

jadi nilai A . B = 4

b. perkalian cross product antara A dan B

(2i + j – k) x (i +3j + k)

A x B = 2i x i + 2i x 3j + 2i x k + j x i + j x 3j + j x k – k x i – k x 3j – k x k  

 A x B = i – j + 6k + (-k) +  (3i) + (-2j)

A x B = 4i – 3j + 5k

baca juga: