SOAL DAN PEMBAHASAN MOMEN GAYA (TORSI) DAN MOMEN INERSIA | 50+ SOAL DINAMIKA ROTASI DAN KESETIMBANGAN BENDA TEGAR

SOAL DAN PEMBAHASAN TORSI ( MOMEN GAYA)  DAN MOMEN INERSIA BENDA TITIK DAN MOMEN INERSIA BENDA TEGAR
FISIKA KELAS XI SEMESTER 2 : BAB DIMANIKA ROTASI DAN KESETIMBANGAN BENDA TEGAR PART 1/3

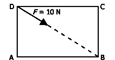
1. Bangun persegi ABCD berikut dengan sisi sisi 20 √2 cm bekerja gaya F seperti pada gambar.  Besarnya torsi F dengan poros di titik A adalah …

a. 2 cmN

b. 2 √2 cmN

c. 4 cmN

d. 20 √2 cm N

e. 200 cmN

JAWAB: E

pembahasan / penyelesaian:
Sudut sudut bujur sangkar = 90⁰ . sehingga sudut antara F dan sisi persigi adalah  Ө  = 45⁰

dengan rumus momen gaya /  torsi berikut:

τ = F . R . sin Ө = 10
. 20 √2 . sin 45⁰ 

τ = 200√2 . ½ √2 = 200 cm.N 

2. Gambar berikut adalah sebuah batang yang ditarik dengan gaya. Momen gaya terhadap titik O adalah . . . .

a. 75 N

b. 50 N

c. 100 √3 N

d. 100 N

e. 250 √3 N

jawab:

pembahasan / penyelesaian:

τ = F . R . sin Ө = 50 . 10 . sin 60⁰ 

τ = 500 . ½ √3 = 250 √3 m.N

3. Perhatikan gambar!

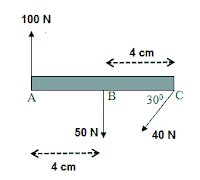
Jika massa batang di abaikan Hitung momen gaya terhadap B

a. 1,2 mN

b. 2,4 mN

c. 3,6 mN

d. 4,8 mN

e. 6,4 mN

Pembahasan:
F_A = 100 N
R_A = AB = 4 cm
τ_A = F_A . R_A = 100 . 4 = 400 cm.N = 4 mN (arah: searah jarum jam)
F_B = 50 N
R_B = 0
τ_B = 0
F_C = 40 N
R_c = 4 cm
θ_C = 30^o
τ_C = F_c.R_c.sin 30^o
τ_C = 40 . 4 . ½
τ_C = 80 cm.N = 0,8 m.N (arah: searah jaum jam)
resultan torsi / momen gaya
Στ = 4 + 0 + 0,8 = 4,8 m.N (searah jarum jam)

4. Perhatikan gambar

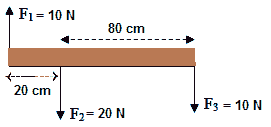
Jika massa batang 2 kg. hitung momen gaya pada batang jika sistem diputar dengan poros di ujung kiri batang (F1)
a. 7 mN

b. 14 mN

c. 21 mN

d. 34 mN

e. 50 mN

Pembahasan:
F1 = 10 N
R1 = 0
τ1 = 0
F2 = 20 N
R2 = 20 cm = 0,2 m
τ2 = F2 . R2 = 20 . 0,2 = 4 m.N (arah: berlawanan jarum jam)
F3 = 10 N
R3 = 100 cm = 1 m
τ3 = 10 . 1 = 10 m.N (arah : berlawanan jarum jam)
w = m.g = 2 . 10 = 20 N
Rw = 50 cm = 0,5 m
τw = 20 . 0,5 = 10 m.N (arah : berlawanan jarum jam)
resultan momen gaya / torsi
Στ = 0 + 4 + 20 + 10 = 34 m.N

5. Perhatikan gambar!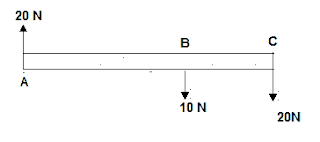

Jika panjang AB = 8 cm dan BC = 2 cm. hitung besar momen gaya batang jika sistem diputar dengan poros dipusat massa (tengah batang)

a. 2 mN

b. 2,3 mN

c. 4 mN

d. 5,5 mN

e. 1,6 mN  

Pembahasan:
Fa = 20 N
Ra = ½ . 10 = 5 cm
τa = 20 . 5 = 100 cm.N (arah : searah jaum jam)
Fb = 10 N
Rb = 5 – 2 = 3 cm
τb = 10 . 3 = 30 cm.N (arah: searah jarum jam)
Fc = 20 N
Rc = ½ . 10 = 5 cm
τc = 20 . 5 = 100 cm.N (arah: seaah jarum jam)
Resultan momen gaya / torsi:
τ = 100 + 30 + 100 = 230 cm . N = 2,3 m.N

6.      Apabila dimensi massa, panjang, dan waktu berturut-turut adalah M, L, dan T, maka dimensi dari momen gaya adalah … .

a. ML^-2 T^-2               d. MT² T^-2

b. ML^-1 T^-2               e. ML² T²

c. MLT^-2

jawab:
pembahasan / penyelesaian:


τ = F . R
τ = [ M L T⁻²][L] = M L² T⁻²

7. sistem benda tegar dirangkai seperti gambar di bawah. agar sembang, maka besarnya F di titik C adalah … .

a. 50 N
b. 80 N
c. 100 N
d. 120 N
e. 180 N
 jawab: C
pembahasan / penyelesaiN:


F₁. R₁ = F₂ . R₂
200 . 4 = F₂ . 8
F₂ = 800 / 8 = 100 N

Artkel Terkait  Pembahasan Fisika UN: Mekanika Fluida

8. Resultan gaya yang sejajar seperti terlihat pada gambar, terletak pada …

a. x = -3
b. x = 0
c. x = 1
d. x = 4
e. x = 8,7
jawab

9.    Tiga buah partikel dengan massa m, 2m, 3m dipasang pada ujung kerangka yang terletak pada bidang xy. Jika sistem diputar terhadap massanya diabaikan. Sistem sumbu y, maka momen inersia sistem adalah ….

a. 5 ma     c. 5 ma²          e. 7 ma²

b. 7 ma     d. 6 ma²

jawab:

pembahasan / penyelesaian:

I = Σ (M . R²) = 3ma² + m. (2a)² 

I = 3ma² +4ma² = 7ma² 

10. sebuah batang silinder homogen dengan panjang 60 cm dan bermassa 4 kg diputar dengan poros di pusat massa. berapakah memen inersia batang tersebut

a. 1200 kg.cm2

b.2400 kg.cm2

c. 3600 kg.cm2

d. 4000 kg.cm2

e. 5000 kg.cm2

jawab: A

penyelesaian / pembahasan:

rumus momen inersia dengan poros di pusat massa (tengah)

I = [1/12] . M . L2

I = [1/12] . 4 (kg). (60 cm)2

I = 1200 kg.cm2

11. sebuah batang silinder homogen dengan panjang 60 cm dan bermassa 4 kg diputar dengan poros di salah satu ujung batang. berapakah memen inersia batang tersebut

a. 1200 kg.cm2

b.2400 kg.cm2

c. 3600 kg.cm2

d. 4800 kg.cm2

e. 5600 kg.cm2

jawab: E

penyelesaian / pembahasan:

rumus momen inersia batang homogen dengan poros di salah satu ujung

I = [1/3] . 4 . 602

I = 4800 kg.cm2

12. sebuah batang silinder homogen dengan panjang 60 cm dan bermassa 4 kg diputar dengan sumbu rotasi / poros  pada jarak 18 cm dari satu ujung batang. berapakah memen inersia batang tersebut

a. 1200 kg.cm2

b.2400 kg.cm2

c. 1776 kg.cm2

Artkel Terkait  Cara Mudah Cek IMEI Xiaomi Untuk Pemula

d. 4800 kg.cm2

e. 5600 kg.cm2

jawab: E

penyelesaian / pembahasan:

diketahui:

d = 30 – 18 = 12 m

rumus momen inersia batang homogen dengan poros pada jarak  dari pusat massa (d)

I = [1/12] . M . L2 + M . d2

I = 1200 + 4 . 122

I = 1200 + 576  = 1776 kg.cm2

Soal dan pembahasan dinamika rotasi dan kesetimbangan benda tegar selanjutnya>>>
> PART 1/3 (momen gaya dan momen inersia)
> PART 2/3 (kesetimbangan partikel, benda tegar, teorema sumbu peralel dan titik berat)
> PART 3/3 (DINAMIKA ROTASI – hubungan torsi dan momen inersia, energi kinetik rotasi, momentum rotasi, kecepatan sudut, percepatan sudut)