Sistem Pertidaksamaan Linear [Soal UN dan Pembahasan]

Pembahasan soal Ujian Nasional (UN) SMA-IPA bidang studi Matematika dengan materi pembahasan Sistem Pertidaksamaan Linear yang meliputi:

• daerah sistem pertidaksamaan linear dan 
• model matematika sistem pertidaksamaan linear.

Konsep 1

Untuk menentukan persamaan garis dari suatu grafik, gunakan konsep berikut ini!

Konsep 2

Untuk menentukan daerah pertidaksamaan, gunakan konsep berikut ini!

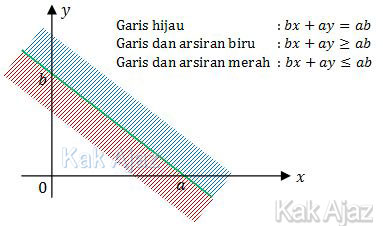
Soal No. 1 tentang Daerah Sistem Pertidaksamaan Linear

Perhatikan gambar berikut!

Daerah yang memenuhi sistem pertidaksamaan linear x + y ≤ 4; x + 4y ≥ 8, x ≥ 0, y ≥ 0 adalah ….

Pembahasan

Berdasarkan konsep pengerjaan soal nomor 2 maka:

Pertidaksamaan (1) adalah x + y ≤ 4. Karena tanda pertidaksamaannya “≤” maka daerah yang diarsir berada di bawah garis (arsiran biru).

Sedangkan pertidaksamaan (2) adalah x + 4y ≥ 8. Karena tanda pertidaksamaannya “≥” maka daerah yang diarsir berada di atas garis (arsiran merah).

Sementara itu, arsiran warna coklat merupakan irisan pertidaksamaan (1) dan (2) di kuadran I (x ≥ 0, y ≥ 0).

Jadi, daerah yang memenuhi sistem pertidaksamaan linear adalah daerah II (B).

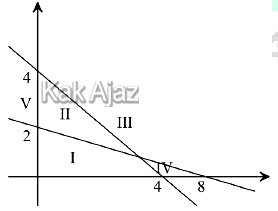
Soal No. 2 tentang Daerah Sistem Pertidaksamaan Linear

Daerah yang memenuhi sistem pertidaksamaan linear 3x + 4y ≤ 96; x + y ≤ 30; x ≥ 0; y ≥ 0 adalah ….

Pembahasan

Kedua pertidaksamaan di atas bertanda “≤” sehingga dapat dipastikan daerah pertidaksamaan keduanya berada di bawah garis.

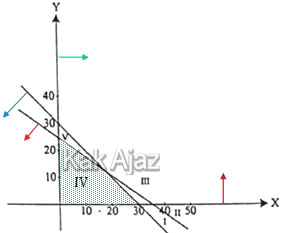
Sementara itu, sistem pertidaksamaan tersebut berada di kuadran pertama (x ≥ 0, y ≥ 0).

Jadi, daerah yang memenuhi sistem pertidaksamaan linear tersebut adalah daerah IV (D).

Soal No. 3 tentang Model Matematika Sistem Pertidaksamaan Linear

Daerah yang diarsir pada gambar di bawah ini adalah daerah himpunan penyelesaian semua (x, y) yang memenuhi sistem pertidaksamaan ….

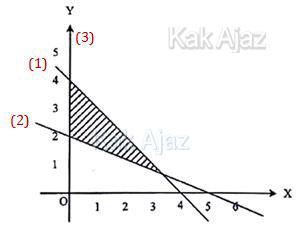
A.	x + y ≤ 4, 2x + 5y ≥ 10, y ≥ 0
B.	x + y ≤ 4, 2x + 5y ≤ 10, y ≥ 0
C.	x + y ≤ 4, 2x + 5y ≥ 10, x ≥ 0
D.	x + y ≥ 4, 2x + 5y ≥ 10, x ≥ 0
E.	x + y ≥ 4, 2x + 5y ≤ 10, x ≥ 0

Artkel Terkait  74 Sinonim Menjelajah dalam Bahasa Indonesia

Pembahasan

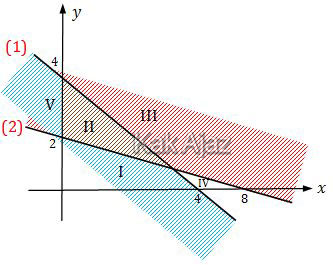
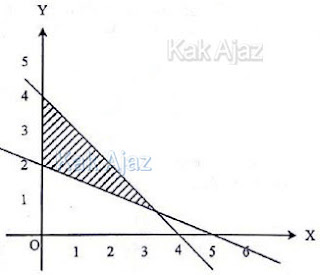
Perhatikan gambar berikut ini!

Daerah arsiran pada grafik di atas dibatasi oleh garis (1), garis (2), dan garis (3).

Garis (1) dan daerah arsiran di bawahnya:

4x + 4y ≤ 16
    x + y ≤ 4

Garis (2) dan daerah arsiran di atasnya:

2x + 5y ≥ 10

Garis (3) atau garis x = 0 (sumbu y) dan daerah di sebelah kanannya:

x ≥ 0

Jadi, daerah himpunan penyelesaian semua (x, y) yang memenuhi sistem pertidaksamaan opsi (C).

Soal No. 4 tentang Model Matematika Sistem Pertidaksamaan Linear

Daerah yang diarsir pada gambar di bawah ini adalah daerah penyelesaian dari pertidaksamaan ….

A.	6x + y ≤ 12; 5x + 4y ≥ 20; x ≥ 0; y ≥ 0
B.	6x + y ≥ 12; 5x + 4y ≥ 20; x ≥ 0; y ≥ 0
C.	6x + y ≥ 12; 5x + 4y ≤ 20; x ≥ 0; y ≥ 0
D.	6x + y ≥ 12; 5x + 4y ≤ 20; x ≥ 0; y ≥ 0
E.	x + 6y ≤ 12; 4x + 5y ≥ 20; x ≥ 0; y ≥ 0

Pembahasan

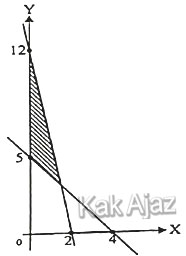
Perhatikan grafik di bawah ini!

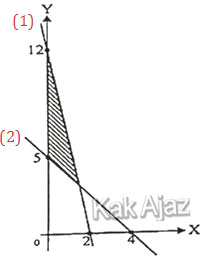
(1)   12x + 2y = 24
(2)   5x + 4y = 20

Persamaan garis (1) perlu disederhanakan, sedangkan persamaan (2) sudah dalam bentuk yang paling sederhana. Sehingga,

(1)   6x + y = 12
(2)   5x + 4y = 20

Daerah yang diarsir terletak di sebelah kiri garis (1) dan di atas garis (2). Tanda pertidaksamaan untuk daerah sebelah kiri adalah “≤” sedangkan daerah atas adalah “≥” . Diperoleh:

(1)   6x + y ≤ 12
(2)   5x + 4y ≥ 20

Daerah arsiran tersebut terletak pada kuadran I sehingga semua x dan y bernilai positif.

x ≥ 0; y ≥ 0

Jadi, daerah yang merupakan daerah penyelesaian dari sistem pertidaksamaan di atas adalah opsi (A).

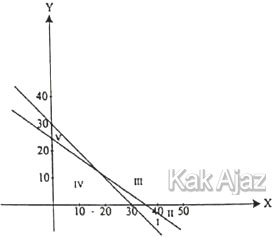
Soal No. 5 tentang Model Matematika Sistem Pertidaksamaan Linear

Perhatikan gambar berikut!

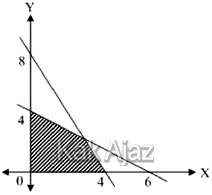
Daerah yang diarsir pada gambar di atas merupakan daerah penyelesaian dari sistem pertidaksamaan ….

A.	x + 2y ≥ 8; 2x + 3y ≥12; x ≥ 0; y ≥ 0
B.	2x + y ≥ 8; 3x + 2y ≥ 12; x ≥ 0; y ≥ 0
C.	2x + y ≤ 8; 2x + 3y ≤ 12; x ≥ 0; y ≥ 0
D.	2x + y ≤ 8; 3x + 2y ≤ 12; x ≥ 0; y ≥ 0
E.	x + 2y ≤ 8; 2x + 3y ≤ 12; x ≥ 0; y ≥ 0

Artkel Terkait  TES LARUTAN PENYANGGA

Pembahasan

Perhatikan gambar berikut ini!

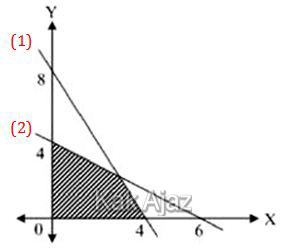
(1)   8x + 4y = 32
(2)   4x + 6y = 24

Jika kedua persamaan di atas disederhanakan maka akan menjadi:

(1)   2x + y = 8
(2)   2x + 3y = 12

Daerah yang diarsir terletak di bawah garis (1) dan di bawah garis (2) sehingga tanda pertidaksamaannya adalah “≤” (kurang dari atau sama dengan).

(1)   2x + y ≤ 8
(2)   2x + 3y ≤ 12

Daerah arsiran tersebut terletak pada kuadran I sehingga semua x dan y bernilai positif.

x ≥ 0; y ≥ 0

Jadi, daerah yang merupakan daerah penyelesaian dari sistem pertidaksamaan di atas adalah opsi (C).

Simak juga:
Pembahasan Matematika IPA UN: Sistem Persamaan Linear 
Pembahasan Matematika IPA UN: Program Linear

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih