Untuk Pembelajaran selanjutnya…
Skala
Skala merupakan perbandingan ukuran atau jarak antara objek pada gambar dengan objek sebenarnya di lokasi. Skala biasanya dimanfaatkan pada pembuatan denah lokasi, rancangan benda, dan peta. Skala dapat dirumuskan sebagai berikut:
![]()
Contoh penggunaan skala pada peta:
- Skala 1 : 1.000.000 artinya tiap 1 cm pada peta mewakili 1.000.000 cm pada jarak sebenarnya
- Jarak kota X dan Y 100 km. Pada peta, jarak kota X dan kota Y hanya 5 cm. Berapa skala peta tersebut?
Penyelesaian:Jarak sebenarnya kota X dan Y = 100 km = 10.000.000 cmJarak peta kota X dan Y = 5 cmMaka: Sehingga skala peta tersebut = 1 : 2. 000.000
Sehingga skala peta tersebut = 1 : 2. 000.000
Faktor Pada Gambar Berskala
Faktor pada gambar berskala adalah perbandingan antara ukuran sisi-sisi gambar/model yang bersesuaian dengan ukuran objek sebenarnya. Faktor pada gambar berskala dapat berupa pengecilan dan perbesaran dengan mengubah ukuran tetapi tidak mengubah bentuk.
- Faktor pengecilan: perbandingan ukuran benda hasil pengecilan dengan ukuran benda mula-mula atau aslinya. Dapat dirumuskan sebagai berikut:
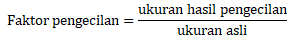
- Faktor perbesaran: perbandingan ukuran benda hasil perbesaran dengan ukuran benda mula-mula atau aslinya. Dapat dirumuskan sebagai berikut:
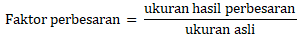
Faktor pengecilan dan perbesaran dapat disebut juga dengan faktor skala, sehingga dapat dirumuskan sebagai berikut: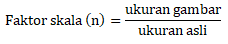
- Untuk n < 1 disebut faktor pengecilan
- Untuk n > 1 disebut faktor perbesaran
Contoh penggunaan faktor skala pada kehidupan sehari-hari:
Tinggi badan seorang anak 125 cm, ketika difoto tinggi badan anak itu hanya 35 cm. Maka faktor skala tersebut adalah …
Penyelesaian:

n = 0,28 ⇒ n < 1, maka faktor skala tersebut adalah faktor pengecilan.
Perbandingan Senilai
Perbandingan senilai merupakan perbandingan dari dua buah objek atau lebih, apabila salah satu variabelnya bertambah maka variable yang lain akan ikut bertambah dan apabila salah satu variabelnya mengecil maka variable yang lain akan ikut mengecil. Kejadian yang tergolong ke dalam perbandingan senilai contohnya adalah:
- Jarak tempuh dengan waktu tempuh
- Jumlah tabungan dengan jangka waktu tabungan
- Jumlah makanan dengan jumlah orang yang makan
- Jumlah karyawan dengan jumlah gaji yang dibayarkan
Pada perbandingan senilai, berlaku rumus sebagai berikut:
![]()
Atau x1 . y2 = x2 . y1
Contoh perhitungan perbandingan senilai:
Stok beras sebuah keluarga sebanyak 35 kg habis dalah waktu 15 hari. Kemudian membeli kembali beras sebanyak 56 kg, maka stok beras tersebut akan habis dalam waktu berapa hari?
Penyelesaian:
Stok beras pertama = x1 = 35 kg
Lama hari pertama = y1 = 15 hari
Stok beras kedua = x2 = 56 kg
Lama hari kedua = y2 = ?
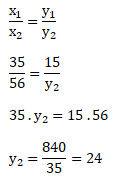
Jadi, lama waktu yang dibutuhkan untuk menghabiskan beras sebanyak 56 kg adalah 24 hari.
Perbandingan Berbalik Nilai
Perbandingan berbalik nilai merupakan perbandingan dari dua buah objek atau lebih, apabila salah satu variabelnya bertambah maka variable akan menurun dan berlaku sebaliknya. Kejadian yang tergolong ke dalam perbandingan berbalik nilai contohnya adalah:
- Jumlah karyawan dengan lama penyelesaian
- Kecepatan kendaraan dengan waktu tempuh
- Jumlah hewan dengan lama waktu menghabiskan makanan
Pada perbandingan berbalik nilai, berlaku rumus sebagai berikut:
![]()
Atau x1 . y1 = x2 . y2
Contoh perhitungan perbandingan berbalik nilai:
Pada sebuah peternakan sebanyak 18 ekor sapi mampu menghabiskan pakan dalam waktu 4 hari. Apabila jumlah sapi ditambah 6 ekor sapi lagi, maka pakan akan habis dalam waktu berapa hari?
Penyelesaian:
Jumlah sapi mula-mula = x1 = 18 ekor
Lama waktu mula-mula = y1 = 4 hari
Jumlah sapi sekarang = x2 = 18 + 6 = 24 ekor
Lama waktu sekarang = y2 = ?
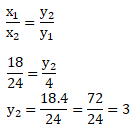
Maka, pakan akan habis dalam waktu 3 hari.
Soal No.1
Jika jumlah siswa laki-laki dan perempuan adalah 26 dan diketahui perbandingan siswa laki-laki dan perempuan yaitu 7 : 6. Maka selisih jumlah siswa laki-laki dan perempuan adalah…
- 1
- 2
- 3
- 4
PEMBAHASAN :
Diketahui
Jumlah total siswa 26
Perbandingan laki-laki dan perempuan = 7 : 6
Menentukan jumlah siswa laki-laki![]()
![]()
![]()
![]()
Maka selisih jumlah siswa laki-laki terhadap perempuan adalah
jumlah laki-laki – jumlah perempuan = 14 – 12 = 2
Jawaban B
Soal No.2
Pada peta diketahui jarak antar kota adalah sejauh 3 cm. Jika digunakan peta dengan skala 1 : 500.000. Maka jarak antar kota tersebut adalah….km
- 15
- 20
- 25
- 30
PEMBAHASAN :
Diketahui skala pada peta = 1 : 500.000
Skala ini menunjukan untuk 1 cm di peta menunjukan 500.000 cm jarak sebenarnya atau 5 km.
Maka untuk 3 cm jarak di peta artinya 3 x 5 km = 15 km jarak sebenarnya
Jawaban A
Soal No.3
Jika pada peta dengan skala 1 : 300 kebun ayah memiliki ukuran 24 cm x 16 cm maka luas tanah ayah yang sebenarnya adalah….m2
- 1.234
- 2.564
- 3.120
- 3.456
PEMBAHASAN :
Perbandingan skala pada peta = 1 : 300 artinya 1 cm mewakili 300 cm atau 3 m
Menentukan panjang tanah
24 cm x 3 m = 72 m
Menentukan lebar tanah
16 cm x 3 m = 48 m
Maka luas tanah tersebut
Luas = Panjang x Lebar = 72 m x 48 m = 3.456 m2
Jawaban D
Soal No.4
Tiang listrik di dekat rumah memiliki panjang 8,1 m. Jika panjang bayangannya diukur maka panjangnya adalah 90 cm. Faktor pengecilnya adalah….
PEMBAHASAN :
Faktor pengecil dapat ditentukan dengan membandingkan ukuran model dalam hal ini bayangan dengan ukuran sebenarnya yaitu tinggi tiang.
tinggi tiang di konversi satuannya agar sama dengan satuan bayangan
8,1 m = 810 cm![]()
Jawaban C
Soal No.5
Andi membeli buku tulis sebanyak 2 lusin uang yang dibayarkan adalah Rp. 70.000. Harga yang harus dibayrkan jika andi membeli 48 buku tulis adalah…
- Rp.85.000
- Rp. 95.000
- Rp. 140.000
- Rp. 150.000
PEMBAHASAN :
1 lusin = 12 buah, maka 2 lusin = 24 buah
24 buah harganya Rp. 70.000
maka untuk 48 buah buku tulis harganya dapat ditentukan lewat perbandingan dengan memisalkan harga 48 buah dengan x![]()
24x = 48 x Rp. 70.000 = 3.360.000![]()
Maka harga untuk 48 buah buku tulis adalah Rp. 140.000
Jawaban C
Soal No.6
Untuk menyelesaikan suatu pekerjaan selama 72 hari diperlukan pekerja sebanyak 24 orang. Setelah dikerjakan selama 30 hari, pekerjaan dihentikan selama 6 hari. Jika kemampuan bekerja setiap orang sama dan agar pekerjaan itu selesai sesuai jadwal semula, maka banyak pekerja tambahan yang diperlukan adalah…orang
- 2
- 4
- 6
- 8
PEMBAHASAN :
Jumlah tenaga total selama 72 hari
72 hari x 24 orang = 1.728
- 30 hari pertama jumlah tenaga yang bekerja
30 hari x 24 orang = 720 - berhenti 6 hari, sedangkan harus selesai selama 72 hari, maka sisa waktunya
(72 – 30 – 6) hari = 36 hari
jumlah tenaga yang diperlukan agar selesai pada waktunya adalah
1.728 – 720 = 1.008
Maka jumlah orang yang diperlukan jika dimisalkan dengan x adalah
(24 + x) orang x 36 hari = 1.008
864 + 36x = 1.008
36 x = 1.008 – 864 = 144![]()
Jawaban B
Soal No.7
Budi berangkat pukul 07.00 naik sepeda dari kota A ke kota B dengan kecepatan 30 km/jam. Pukul 09.00 dari tempat yang sama, Dimas menggunakan sepeda motor dengan kecepatan tetap 60 km/jam. Dimas dapat menyusul Budi pada….
- pukul 10.00
- pukul 10.30
- pukul 11.00
- pukul 11.30
PEMBAHASAN :
Jika digambarkan dalam sebuah tabel
Maka dimas akan menyusul pada jam 11.00
Jawaban C
Soal No.8
Sebuah mesin penggilingan padi dari pukul 06.00 sampai pukul 09.00 mampu menggiling 12 kuintal padi. Setelah istirahat sejam, pekerjaan tersebut dilanjutkan kembali sampai pukul 18.00 maka hasil gilingan padi seluruhnya adalah….
- 32 kuintal
- 36 kuintal
- 38 kuintal
- 44 kuintal
PEMBAHASAN :
Pada sesi ke-1 dari jam 06.00 s.d 09.00 (3 jam) menghasilkan 12 kuintal
Pada sesi ke-2 dari jam 10.00 s.d 18.00 (8 jam) menghasilkan x kuintal
Untuk menentukan berat hasil gilingan padi nya dapat ditentukan lewat perbandingan![]()
3x = 12 x 8 = 96![]()
Jawaban A
Soal No.9
Sejenis gas dengan berat tertentu, volume gasnya berbanding terbalik dengan tekanan. Bila gas tersebut bertekanan 1,5 atmofer maka volumenya menjadi 60 cm3. Bila volumenya diperbesar menjadi 150 cm3. maka tekanan gas menjadi….
- 0,374 atm
- 0,6 atm
- 3,75 atm
- 6 atm
PEMBAHASAN
Diketahui
Tekanan 1,5 atm maka volumenya 60 cm3
Untuk volume 150 cm3 tekanannya diperoleh melalui perbandingan, karena berbanding terbalik maka:![]()
![]()
150.P2 = 60. 1,5 = 90![]()
Jawaban B
Soal No.10
Satu buah pak cokelat akan dibagikan kepada 24 anak, setiap anak mendapatkan 8 cokelat. Jika cokelat tersebut akan dibagikan 16 anak, banyak cokelat yang diperoleh setiap anak adalah….cokelat
- 8
- 12
- 16
- 48
PEMBAHASAN :
Diketahui
1 pak diberikan ke 24 anak, masing-masing mendapatkan 8 cokelat
maka untuk 16 anak akan memperoleh cokelat masing-masing lewat perbandingan
Hubungannya berbanding terbalik karena semakin banyak anak yang dibagi semakin sedikit coklat yang diperoleh masing-masing anak![]()
![]()
16x = 24 x 8 = 192![]()
Jawaban B
Soal No.11
Dani dan Ahmad mempunyai sejumlah uang dengan perbandingan 3 : 4. Selisih jumlah uang Dani dan Ahmad adalah Rp 100.000,00. Maka jumlah uang yang dimiliki Dani adalah sebesar …
- Rp 300.000,00
- Rp 450.000,00
- Rp 230.000,00
- Rp 550.000,00
PEMBAHASAN :
Diketahui:
Perbandingan jumlah uang Dani dan Ahmad adalah 3 : 4
Menentukan jumlah uang Dani bisa ditentukan dengan cara: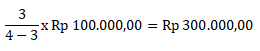
Maka uang yang dimiliki Dani sebesar Rp 300.000,00.
Jawaban A
Soal No.12
Seorang pedagang menjual buah pepaya dan jeruk. Jumlah pepaya 65% dari total jumlah buah dalam peti, sedangkan jumlah jeruk 35% dari total jumlah buah dalam peti. Maka perbandingan jumlah buah pepaya dan jeruk adalah …
- 11 : 5
- 12 : 7
- 13 : 3
- 13 : 7
PEMBAHASAN :
Diketahui:
Jumlah pepaya = 65%
Jumlah jeruk = 35%
Maka perbandingannya: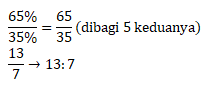
Jawaban D
Soal No.13
Suatu bilangan pecahan memiliki perbandingan pembilang dan penyebut 5 : 13 dengan jumlah pembilang dan penyebut adalah 90. Maka nilai bilangan pecahan tersebut adalah …
- 30 : 60
- 45 : 45
- 25 : 65
- 10 : 80
PEMBAHASAN :
Nilai pembilang = 5![]()
Nilai penyebut = 13![]()
Maka nilai bilangan pecahan tersebut adalah 25 : 65
Jawaban C
Soal No.14
Jarak kota A dan kota B adalah 72 km dengan skala 1: 1.200.000. Maka jarak dua kota tersebut pada peta adalah …
- 5 cm
- 6 cm
- 7 cm
- 8 cm
PEMBAHASAN :
Jarak sebenarnya = 72 km = 7.200.000 cm
Skala pembuatan peta = 1 : 1.200.000
Maka jarak kedua kota pada peta adalah: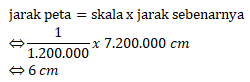
Jawaban B
Soal No.15
Sebuah perkebunan berbentuk persegi panjang digambarkan pada peta dengan skala 1 : 300. Ukuran perkebunan tersebut pada peta menjadi 10 cm x 6 cm. Setiap 2 m2 pada perkebunan tersebut ditanami pohon pinus. Sehingga banyak pohon pinus yang ditanam adalah …
- 270 pohon pinus
- 300 pohon pinus
- 320 pohon pinus
- 410 pohon pinus
PEMBAHASAN :
Diketahui:
Skala peta = 1 : 300
Ukuran pada peta :
Panjang = 10 cm
Lebar = 6 cm
Jarak tanam pohon pinus = 2 m2
Menentukan panjang dan lebar sebenarnya: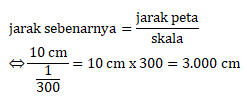
Panjang sebenarnya = 3.000 cm = 30 m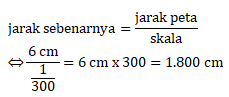
Lebar sebenarnya = 1.800 cm = 18 m
Menentukan luas kebun:
L = p x l
⇔ 30 m x 18 m
⇔ 540 m2
Maka banyak pohon pinus yang ditanam adalah sebanyak = 540 m2 : 2 m2 = 270 pohon pinus.
Jawaban A
Soal No.16
Bentuk paling sederhana dari 4 jam : 60 menit adalah …
- 1 : 4
- 4 : 1
- 3 : 1
- 2 : 1
PEMBAHASAN :
Diketahui:
1 jam = 60 menit, maka 4 jam = 4 x 60 menit = 240 menit
Maka perbandingannya = 240 menit : 60 menit = 4 : 1
Jawaban A
Soal No.17
PEMBAHASAN :
Menyederhanakan pecahan tersebut adalah sebagai berikut: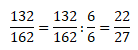
Jadi, bentuk paling sederhana dari pecahan tersebut adalah ![]()
Jawaban C
Soal No.18
Harga sebuah motor Rp 12.500.000,00 dan harga sepeda Rp 5.000.000,00. Perbandingan harga motor dan harga sepeda adalah …
- 4 : 3
- 5 : 2
- 7 : 5
- 8 : 3
PEMBAHASAN :
Diketahui:
Harga motor = Rp 12.500.000,00
Harga sepeda = Rp 5.000.000,00
Maka perbandingannya:![]()
Jawaban B
Soal No.19
Pada sebuah peta jarak 5 cm mewakili 45 km pada jarak sebenarnya. Besar skala yang digunakan pada pembuatan peta tersebut adalah …
- 1 : 1.000.000
- 1 : 900.000
- 1 : 1.500.000
- 1 : 800.000
PEMBAHASAN :
Diketahui:
Jarak peta = 5 cm
Jarak sebenarnya = 45 km = 4.500.000 cm
Maka skalanya adalah: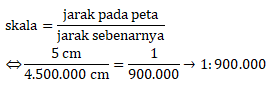
Jawaban B
Soal No.20
Sebuah lapangan sepak bola berukuran panjang 90 m dan lebar 72 m. Kemudian lapangan tersebut dibuatkan gambar dengan skala sehingga panjangnya menjadi 6 cm dan lebarnya menjadi … cm
- 5 cm
- 2,9 cm
- 4,8 cm
- 6 cm
PEMBAHASAN :
Diketahui:
Panjang sebenarnya = 90 m = 9.000 cm
Panjang gambar = 6 cm
Lebar sebenarnya = 72 m = 7.200 cm
Menghitung skala lapangan, sebagai berikut:
Maka lebar peta dapat dihitung sebagai berikut: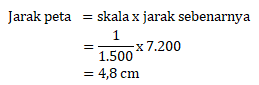
Jawaban C
Soal No.21
Jarak dari kota A ke kota B pada peta adalah 6,2 cm dengan skala 1 : 1.500.000. Pada setiap 35 km memerlukan 1 liter bensin, maka bensin yang diperlukan untuk sampai ke kota B adalah … liter.
- 1
- 1,9
- 2
- 2,7
PEMBAHASAN :
Diketahui:
Jarak kota A ke kota B pada peta = 6,2 cm
Skala pada peta = 1 : 1.500.000
Perjalanan 35 km membutuhkan bensin 1 liter
Menentukan jarak kota A ke kota B yang sebenarnya: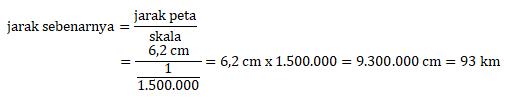
Maka, banyak bensin yang dibutuhkan untuk sampai ke kota B ![]()
Jawaban D
Soal No.22
Sebuah foto berukuran 6 cm x 9 cm akan diperbesar 3 kali. Maka keliling foto tersebut setelah diperbesar adalah …
- 100 cm
- 90 cm
- 80 cm
- 70 cm
PEMBAHASAN :
Diketahui:
Ukuran foto = 6 cm x 9 cm
Perbesaran 3 kali
Menentukan panjang dan lebar foto setelah diperbesar:
6 cm diperbesar 3 kali, sehingga 6 cm x 3 = 18 cm (panjang foto)
9 cm diperbesar 3 kali, sehingga 9 cm x 3 = 27 cm (lebar foto)
Maka keliling foto tersebut adalah:
K = 2 (p + l) = 2 (18 cm + 27 cm) = 90 cm
Jawaban B
Soal No.23
Terdapat kota X, Y, dan Z yang terletak pada satu garis lurus. Jarak kota X ke kota Y pada peta adalah 5 cm sedangkan jarak kota Y ke kota Z pada peta adalah 6 cm. Dengan skala 1 : 1.350.000 jarak kota X ke kota Z yang sebenarnya adalah …
- 88,5 km
- 148,8 km
- 97,6 km
- 102,9 km
PEMBAHASAN :
Diketahui:
Jarak kota X ke kota Y pada peta = 5 cm
Jarak kota Y ke kota Z pada peta = 6 cm
Skala pada peta = 1 : 1.350.000
Menentukan jarak kota X ke kota Y yang sebenarnya: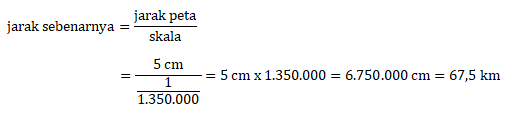
Menentukan jarak kota Y ke kota Z yang sebenarnya:
Maka jarak kota X ke kota Z sebenarnya = jarak kota X ke kota Y sebenarnya + jarak kota Y ke kota Z sebenarnya
⇔ 67,5 km + 81 km
⇔ 148,8 km
Jawaban B
Soal No.24
Sebuah lahan perkebunan yang berbentuk persegi digambarkan pada peta panjang sisinya 8 cm dengan skala 1 : 550. Di sekeliling kebun akan dibuatkan pagar, maka panjang pagar tersebut adalah …
- 125 m
- 136 m
- 149 m
- 176 m
PEMBAHASAN :
Diketahui:
Panjang sisi persegi pada peta = 8 cm
Skala pada peta = 1 : 550
Menentukan panjang sisi kebun sebenarnya: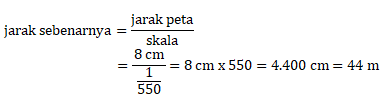
Maka panjang pagar yang dibutuhkan untuk mengelilingi kebun adalah:
Keliling kebun = 4 x 44 m = 176 m
Jawaban D
Soal No.25
Seorang arsitek merancang model sebuah rumah dengan ukuran panjang 32 cm dan lebar 24 cm. Panjang rumah sebenarnya adalah 20 m, maka lebar rumah sebenarnya adalah …
- 15 m
- 16 m
- 17 m
- 18 m
PEMBAHASAN :
Diketahui:
Panjang model = 32 cm
Lebar model = 24 cm
Panjang sebenarnya = 20 m = 2.000 cm
Menentukan faktor skala:![]()
Maka lebar sebenarnya adalah: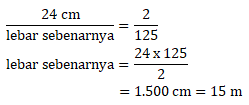
Jawaban A
Soal No.26
Sebuah menara muncul di acara televisi dan hanya memiliki tinggi 20 cm. Apabila faktor pengecilannya adalah 1/320 maka tinggi menara yang sebenarnya adalah … m.
- 55
- 58
- 64
- 72
PEMBAHASAN :
Diketahui:
Tinggi menara di televisi = 20 cm
Faktor pengecilan = 1/320
Maka tinggi menara yang sebenarnya dapat dihitung sebagai berikut:
Jawaban C
Soal No.27
Denah sebuah taman yang berbentuk persegi panjang memiliki ukuran 12 cm x 10 cm, dengan faktor pengecilan 1/120. Maka luas taman sebenarnya adalah … m2 .
- 102,5
- 135,7
- 172,8
- 178,1
PEMBAHASAN :
Diketahui:
Ukuran denah taman = 12 cm x 10 cm
Factor pengecilan = 1/120![]()
Menentukan panjang taman sebenarnya:
Menentukan lebar taman sebenarnya:
Maka luas sebenarnya taman tersebut:
Luas taman = 14,4 m x 12 m
⇔ 172,8 m2
Jawaban C
Soal No.28
8 buah semangka dijual dengan harga Rp 160.000,00. Sedangkan untuk 15 semangka harganya adalah …
- Rp 500.000,00
- RP 400.000,00
- Rp 300.000,00
- Rp 200.000,00
PEMBAHASAN :
Diketahui:
8 buah semangka, maka total harga = Rp 160.000,00
15 buah semangka, dimisalkan total harga = x
Maka nilai x adalah:
Jawaban C
Soal No.29
Harga 3 kardus minuman ringan Rp 72.000,00. Dalam satu kardus berisi 10 botol minuman ringan. Dengan uang Rp 57.600,00 berapa botol minuman yang akan diperoleh …
- Rp 45.400,00
- Rp 52.800,00
- Rp 57.600,00
- Rp 60.600,00
PEMBAHASAN :
Diketahui:
3 kardus = Rp 72.000,00
1 kardus = 10 botol
uang untuk membeli minuman ringan = Rp 57.600,00
Menentukan harga satuan minuman ringan:
Jumlah botol minuman ringan = 3 kardus x 10 botol = 30 botol
Jawaban C
Soal No.30
Harga kunyit per pon adalah Rp 12.500,00. Harga untuk 18 kg kunyit adalah …
- Rp 350.000,00
- Rp 450.000,00
- Rp 550.000,00
- Rp 650.000,00
PEMBAHASAN :
Diketahui:
Harga kunyit per pon = Rp 12.500,00
1 kg = 2 pon, maka 1 pon = 0,5 kg
18 kg kunyit = Rp x
Maka nilai x adalah:
Jawaban B
Soal No.31
Sebuah benda dengan tinggi 15 cm di letakkan di depan sebuah proyektor sehingga membentuk bayangan setinggi 35 cm, maka nilai faktor perbesarannya adalah …
- 2,3
- 2,0
- 1,7
- 1,3
PEMBAHASAN :
Diketahui:
Tinggi benda sebenarnya = 15 cm
Tinggi benda setelah perbesaran = 35 cm
Maka faktor perbesarannya dapat dihitung sebagai berikut: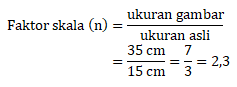
Jawaban A
Soal No.32
Patung dengan tinggi 4,8 m memiliki tinggi bayangan 120 cm. Maka factor pengecilannya adalah …
- 0,11
- 0,18
- 0,22
- 0,25
PEMBAHASAN :
Diketahui:
Tinggi patung = 4,8 m = 480 cm
Tinggi bayangan patung = 120 cm
Maka faktor pengecilannya dapat dihitung sebagai berikut: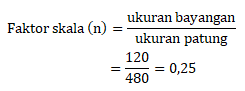
Jawaban D
Soal No.33
Di sebuah pabrik 1 unit mesin dapat menghasilkan 1 kodi selama 4 jam, maka banyak barang yang dihasilkan oleh 3 unit mesin selama 6 jam adalah … kodi.
- 3
- 4
- 4,5
- 5,5
PEMBAHASAN :
Diketahui:
1 unit mesin → 1 kodi → 4 jam
3 unit mesin → x kodi → 6 jam
Penyelesaian I:
1 mesin → 4 jam → 1 kodi
3 mesin → 4 jam → x kodi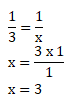
Penyelesaian II:
3 mesin → 4 jam → 3 kodi
3 mesin → 6 jam → y kodi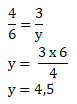
Maka banyak barang yang dihasilkan 3 unit mesin selama 6 jam = 4,5 kodi.
Jawaban B
Soal No.34
Sebuah kendaraan melakukan perjalanan sejauh 150 km. Diketahui setiap 42 km menghabiskan bensin sebanyak 2 liter dan harga satu liter bensin Rp 6.500,00. Maka uang yang dibutuhkan untuk membeli adalah …
- Rp 35.140,00
- Rp 38.180,00
- Rp 42.500,00
- Rp 46.150,00
PEMBAHASAN :
Diketahui:
Jarak perjalanan = 150 km, menghabiskan bensin x liter
Setiap 42 km, menghabiskan bensin 2 liter
1 liter bensin = Rp 6.500,00
Menghitung nilai x (jumlah volume bensin), sebagai berikut: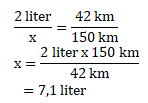
Maka uang yang dibutuhkan untuk membeli bensin = 7,1 liter x Rp 6.500,00 = Rp 46.150,00
Jawaban D
Soal No.35
Suatu proyek pembangunan sebuah gedung memerlukan 10 orang pekerja untuk menyelesaikan pekerjaan dalam waktu 30 hari. Kemudian ada 4 orang pekerja yang sakit dan tidak meneruskan pekerjaannya. Maka proyek tersebut akan terlambat berapa hari dari jadwal yang telah ditentukan selama … hari.
- 10
- 20
- 30
- 40
PEMBAHASAN :
Diketahui:
10 pekerja memerlukan waktu 30 hari
10 – 4 = 6 pekerja memerlukan waktu x hari
Dengan perbandingan berbalik nilai:
Maka proyek tersebut akan terlambat selama = 50 hari – 30 hari = 20 hari
Jawaban D
Soal No.36
Seorang pelanggan akan membeli beras sebanyak 8 kg dengan harga Rp 56.000,00. Akan tetapi harga beras telah mengalami kenaikan sebesar 15%. Maka pelanggan tersebut akan memperoleh beras sebanyak … kg.
- 5
- 6
- 7
- 8
PEMBAHASAN :
Diketahui:
8 kg beras harganya Rp 56.000,00
Persentase kenaikan = 15%
Harga beras per kilo = Rp 56.000,00 : 8 kg = Rp 7.000,00
Setelah kenaikan, harga beras per kilo = (100% + 15%) x Rp 7.000,00 = Rp 8.050,00
Dengan perbandingan berbalik nilai:
Misalkan: a = banyak beras yang diperoleh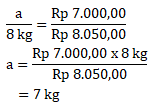
Jawaban C
Soal No.37
Enam ekor kambing mampu menghabiskan pakan selama 10 hari. Apabila jumlah kambing bertambah menjadi 10 ekor kambing maka pakan akan habis dalam waktu … hari.
- 3
- 4
- 5
- 6
PEMBAHASAN :
Diketahui:
6 ekor pakan habis selama 12 hari
10 ekor kambing pakan habis selama p hari
Dengan perbandingan berbalik nilai: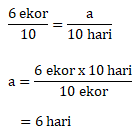
Jawaban D
Soal No.38 (UAN)
Sebuah mobil bergerak dengan kecepatan rata-rata 60 km/jam dapat menempuh jarak dari kota P ke kota Q dalam waktu 5 jam. Jika jarak kedua kota ingin ditempuh dalam waktu 4 jam maka kecepatan rata-rata mobil seharusnya … km/jam.
- 65
- 70
- 75
- 80
PEMBAHASAN :
Diketahui:
Kecepatan 60 km/jam untuk perjalanan 5 jam
Kecepatan p km/jam untuk perjalanan 4 jam
Catatan: Waktu berbanding terbalik dengan kecepatan
Dengan perbandingan berbalik nilai: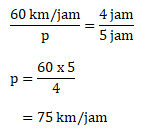
Jawaban C
Soal No.39 (UAN 2007)
Seorang pemborong memperkirakan dapat menyelesaikan suatu pekerjaan dalam waktu 20 hari dengan 22 orang pekerja. Jika pemborong ingin menyelesaikan pekerjaan tersebut dalam waktu 11 hari, banyaknya pekerja tambahan yang diperlukan adalah … orang.
- 65
- 70
- 75
- 80
PEMBAHASAN :
Diketahui:
20 hari selesai 22 pekerja
11 hari selesai 22 + x pekerja
Dengan perbandingan berbalik nilai:
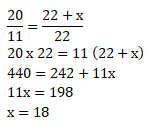
Maka banyak pekerja tambahan yang diperlukan adalah 18 orang
Jawaban C
Soal No.40
Di sebuah peternakan sapi persediaan rumput untuk 300 ekor akan habis dalam waktu 20 hari. Kemudian sebanyak 100 ekor sapi terjual, maka persediaan rumput akan mencukupi untuk … hari.
- 30
- 25
- 20
- 15
PEMBAHASAN :
Diketahui:
300 ekor sapi menghabiskan rumput selama 20 hari
300 ekor – 100 ekor = 200 ekor menghabiskan rumput selama x hari
Dengan perbandingan berbalik nilai: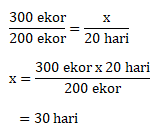
Jawaban A
Semoga Bermanfaat