Rangkuman Materi, Contoh Soal & Pembahasan Persamaan Garis Lurus SMP

Pengertian Persamaan Garis Lurus

Persamaan garis lurus merupakan suatu persamaan garis pada koordinat y dan koordinat x yang terletak pada sebuah garis. Sedangkan garis lurus adalah kumpulan dari titik-titik yang sejajar.

Contoh:

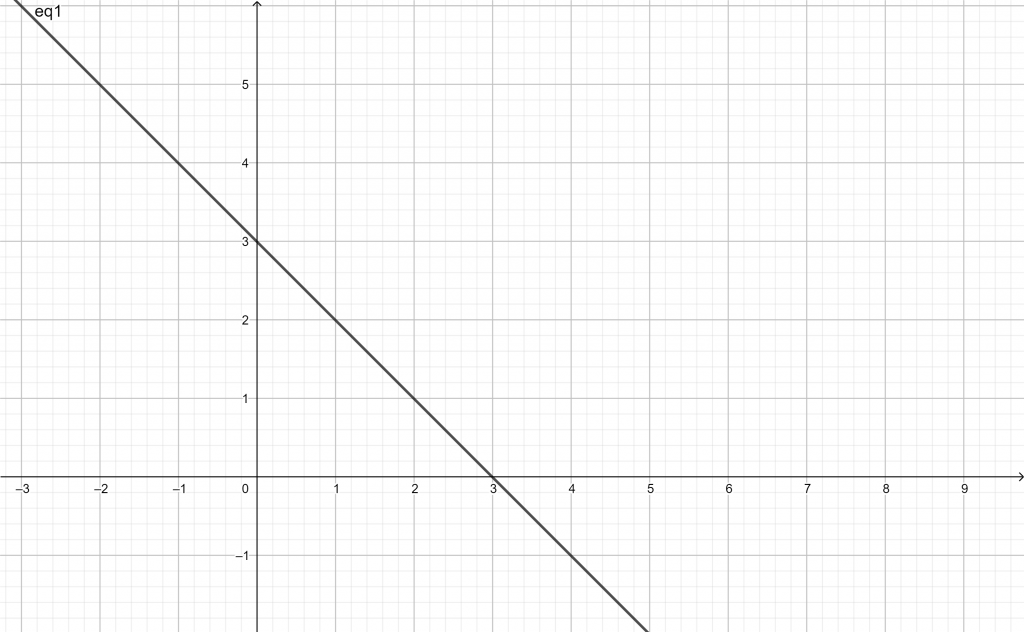
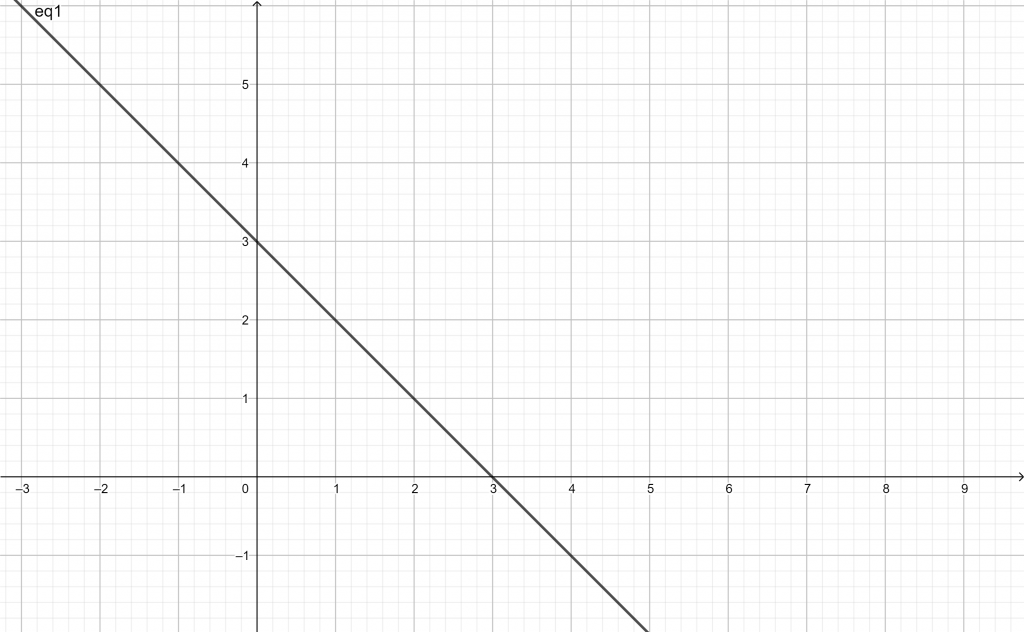
Persamaan garis y + x = 3 terletak pada koordinat kartesius, gambarkan pada bidang kartesius!

Pembahasan:

Menentukan titik potong pada sumbu x dan sumbu y

Titik potong sumbu x, y = 0

y + x = 3

0 + x = 3

x = 3, (3,0)

titik potong sumbu y, x = 0

y + x = 3

y + 0 = 3

y = 3, (0,3)

Maka gambar yang terbentuk sebagai berikut:

Pengertian Gradien

Gradien adalah nilai yang dihasilkan dari perbandingan ordinat dan absis yang menyatakan kemiringan suatu garis. Gradien dilambangkan dengan huruf m dan dapat dirumuskan sebagai berikut:

Beberapa cara untuk menentukan gradien pada suatu persamaan garis:

1. Gradien pada garis y = mx
   Pada persamaan garis y = mx, gradien sama dengan koefisien variable x. contohnya:
   Persamaan garis 3x – 5y = 0
   Maka, gradien adalah:
   

2. Gradien pada garis y = mx + c
   Jadikan persamaannya menjadi bentuk y = mx + c, contohnya: 6 – 3y = 4x
   Pembahasan:
   6 – 3y = 4x
   – 3y = 4x – 6
   – 3y = 4x – 6 (dibagi – 3)
   Maka gradiennya yaitu:
   

3. Gradien pada garis ax + by + c = 0
   Gradien garis dengan persamaan ax + by + c = 0 harus diubah menjadi bentuk y = mx + c, contohnya: 3x + y + 5 = 0Pembahasan:
   3x + y + 5 = 0
   y = – 3x – 5
   Maka, m = – 3

4. Gradien yang melalui dua titik
   Misalkan gradien  yang melalui dua titik P dan Q dengan P (x₁ , y₁ ) dan (x₂ , y₂ ) maka rumus  gradien yang berlaku sebagai berikut:
   Contohnya:
   Titik (2,3) dan titik (3,5)Pembahasan:
   Sehingga gradien dari kedua titik tersebut m = 2

Sifat-Sifat Gradien

Gradien memiliki sifat-sifat seperti di bawah ini:

1. Apabila suatu garis sejajar dengan sumbu x maka nilai gradiennya adalah nol (m = 0)
   
2. Apabila suatu garis sejajar dengan sumbu y maka garis tersebut tidak memiliki gradien
   
3. Setiap garis yang sejajar memiliki gradien yang sama (m_PQ = m_AB )
   
4. Hasil kali gradien dari dua garis yang saling tegak lurus adalah – 1 (m_PQ x m_AB = – 1)
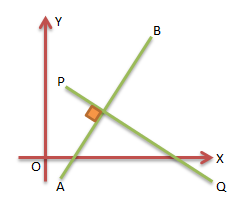
5. Apabila garis naik dari kiri ke kanan maka gradiennya bernilai positif (m > 0)
   
6. Apabila garis turun dari kiri ke kanan maka gradiennya bernilai negative (m < 0)
   

Menentukan Persamaan Garis Lurus

Beberapa cara untuk menentukan persamaan garis lurus sebagai berikut:

1. Persamaan garis lurus bentuk umum (y = mx) yaitu persamaan melalui titik pusat (0,0) dan bergradien. Contohnya:
   Diketahui:
   Persamaan melalui titik pusat (0,0)
   Gradien = 3Maka persamaannya menjadi:
   y = mx
   y = 3x

2. Persamaan garis lurus y = mx + c
   • Persamaan garis yang sejajar dengan y = mx dan bergradien = m
   • Persamaan garis melalui (0,c) dan bergradien m. (0,c) = titik potong sumbu y.
   • Contohnya:
     Diketahui titi garis (0,3) , m = 2
     y = mx + c
     y = 2x + 3

3. Persamaan garis lurus melalui titik (x₁ , y₁ ) dan bergradien m ® apabila diketahui gradien dan salah satu titik kordinatnya. Rumus yang berlaku adalah sebagai berikut:
   y – y₁ = m (x – x₁ )Contohnya:
   Diketahui: titik kordinat (0,3) dan m = 2Maka persamaannya sebagai berikut:
   y = mx + c
   y = 2x + 3

4. Persamaan garis lurus melalui dua titik yaitu (x₁ , y₁ ) dan (x₂ , y₂ ), apabila diketahui dua titik kordinatnya. Rumus yang berlaku adalah sebagai berikut:
   Contoh:
   Persamaan garis melalui titik P (2,5) dan Q (-3,4), maka persamaan garisnya sebagai berikut:
   

Menentukan Titik Potong

Untuk menentukan titik potong dari dua persamaan garis bisa ditentukan dengan cara grafik dan substitusi.

1. Grafik
   Menentukan titik potong dengan grafik dilakukan dengan memisalkan x = 0 untuk mendapatkan perpotongan grafik pada sumbu y dan memisalkan y = 0 untuk mendapatkan perpotongan grafik pada sumbu x.
   Contohnya:
   Menentukan titik potong antara garis y = 2x + 3 dan y = x + 4Pembahasan:
   Persamaan 1:
   y = 2x + 3sumbu x, y = 0
   2x + 3 = 0Sumbu y, x = 0
   y = 2x + 3
   y = 2(0) + 3
   y = 3 → (0,3)Persamaan 2:
   y = x + 4sumbu x, y = 0
   x + 4 = 0
   x = – 4 → (- 4,0)sumbu y, x = 0
   y = x + 4
   y = 0 + 4
   y = 4 → (0,4)
   Maka titik potong dapat diketahui pada grafik di bawah ini:
   
   Dari grafik di atas diperoleh titik potongnya = (1,5)

2. Substitusi
   Persamaan satu disubstitusikan ke persamaan dua atau sebaliknya. Apabila dua buah garis tidak saling sejajar maka garis tersebut akan berpotongan di suatu titik tertentu.  Contohnya menentukan titik potong antara garis y = 2x + 3 dan y = x + 4 sebagai berikut:
   y = x + 4 substitusikan ke y = 2x + 3
   sehingga: y = 2x + 3
   ⇔ x + 4 = 2x + 3
   ⇔ – x = -1
   ⇔ x = 1
   Dan y = 2x + 3
   ⇔ y = 2.1 + 3
   ⇔ y = 5
   Titik potongnya adalah (1,5)

Soal No.1

Jika diketahui sebuah garis dengan persamaan 3y – x + 4 = 0. Jika y = 3, maka nilai x adalah…

1. 5
2. 6
3. 7
4. 8

PEMBAHASAN :
Diketahui persamaan garis 3y – x + 4 = 0 dengan y = 3
Substitusikan nilai y ke persamaan
3. 3 – x + 4 = 0
9 – x + 4 = 0
-x = 4 – 9 = -5 ….dikalikan -1
x = 5
Jawaban A

Soal No.2

Gradien dari garis 2y + x = 6 adalah….

1. -1
2. -½
3. 1
4. 2

PEMBAHASAN :
Persamaan 2y + x = 6 diubah bentuknya menjadi y = mx + c
Menjadi
2y = -x + 6…..dibagi 2
y = -½x + 3
maka gradiennya adalah -½
Jawaban B

Soal No.3

Jika sebuah garis memiliki persamaan 5y + 6x – 12 = 0. Maka koordinat titik potong terhadap sumbu x adalah….

1. (-2, 0)
2. (-1, 0)
3. (1, 0)
4. (2, 0)

PEMBAHASAN :
Agar memiliki titik potong terhadap sumbu x maka syaratnya y = 0
5y + 6x – 12 = 0
5.0 + 6x – 12 = 0
6x – 12 = 0
6x = 12
x = 2
Maka koordinat titik potong terhadap sumbu x adalah (2, 0)
Jawaban D

Soal No.4
Gradien persamaan garis yang melalui titik (3,6) dan (6, 9) adalah….

1. 1. ½
   2. 1
   3. 3
   4. 5

PEMBAHASAN :
Menentukan gradien garis yang melalui titik (x₁, y₁) dan (x₂, y₂) adalah:

Jawaban B

Soal No.5

Garis a sejajar dengan garis b. Jika diketahui persamaan garis a adalah 4y + 2x – 7 = 0. Maka gradien garis b adalah…

1. -2
2. -1
3. -½
4. 1

PEMBAHASAN :
Garis a dan b sejajar, maka:
gradien garis a = gradien garis b
Menentukan gradien garis a
4y + 2x – 7 = 0
diubah ke bentuk y = mx + c
4y = -2x + 7
y = -½x +
maka gradien garis a = gradien garis b = -½
Jawaban C

Soal No.6

Persamaan garis yang memiliki gradien 3 dan melewati titik (2,4) adalah…

1. 2y + 3x +8 = 0
2. y – 3x + 2 = 0
3. y + 3x -2 = 0
4. 2y – 3x – 8 = 0

PEMBAHASAN :
Menentukan persamaan garis yang memiliki m = 3 melewati titik (2, 4)
y – y₁ = m(x – x₁)
y – 4 = 3(x – 2)
y – 4 = 3x – 6
y – 4 – 3x + 6 = 0
y – 3x + 2 = 0
Jawaban B

Soal No.7

Titik (2,4) dan (5,8) persamaan garis lurus yang terbentuk adalah….

1. 3y + 4x – 4 = 0
2. 2y + 4x – 4 = 0
3. 2y – 4x + 4 = 0
4. 3y – 4x – 4 = 0

PEMBAHASAN :
Menentukan persamaan garis lurus dari dua titik yang diketahui menggunakan rumus:



3(y – 4) = 4(x – 2)
3y – 12 = 4x – 8
3y – 4x – 12 + 8 = 0
3y – 4x – 4 = 0
Jawaban D

Soal No.8

Koordinat titik potong garis 3x + 2y = 5 dan 3x + 4y =-7 adalah….

PEMBAHASAN :
Menentukan titik potong dapat dicari dengan menentukan nilai x dan y melalui penyelesaian sistem persamaan linear dua variabel
Menentukan y dengan mengeliminasi x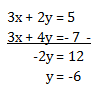

Menentukan x dengan mensubstitusikan nilai y ke salah satu persamaan
3x + 2y = 5
3x + 2(-6) = 5
3x – 12 = 5
3x = 5 + 12 = 17
x =
Maka koordinat titik potongnya adalah

Jawaban C

Soal No.9

Titik (4, a) dilalui oleh garis 4x – 6y = 8.Maka nilai a adalah….

PEMBAHASAN 
Titik (4, a) dilalui garis 4x – 6y = 8, substitusikan titik tersebut ke persamaan garis
4.4 – 6.a = 8
16 – 6a = 8
-6a = 8 – 16 = 8
a =
Jawaban B

Soal No.10

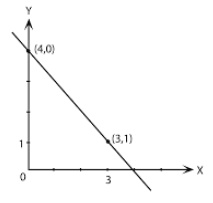
Persamaan garis pada gambar berikut adalah….

1. y + x – 4 = 0
2. 2x – y – 2 = 0
3. x + 2y – 5 = 0
4. x – y – 2 = 0

PEMBAHASAN :
Dari gambar diketahui persamaan garis melalui dua titik yaitu (4, 0) dan (3, 1). Maka persamaan garisnya dapat ditentukan dengan rumus:


y = -(x -4)
y = -x + 4
y + x – 4 = 0
Jawaban A

Soal No.11

Sebuah garis dengan persamaan y = 2x – 7. Apabila garis tersebut memiliki absis = 5 maka ordinatnya adalah …

1. 1
2. 2
3. 3
4. 4

PEMBAHASAN :
Persamaan garisnya  y = 2x – 7
Absis = titik pada sumbu x = 5
Ordinat = titik pada sumbu y

Maka untuk mencari nilai ordinat, substitusikan nilai x pada persamaan garis sebagai berikut:
y = 2x -7
y = 2(5) – 7
y = 3
Jawaban C

Soal No.12

Nilai gradien dari persamaan garis 5y = 3x adalah …

PEMBAHASAN :
Gradien adalah nilai yang dihasilkan dari perbandingan ordinat dan absis yang menyatakan kemiringan suatu garis. Pada persamaan garis y = mx, gradien sama dengan koefisien variable x. sehingga gradien pada persamaan 5y = 3x sebagai berikut:
5y = 3x

Jawaban C

Soal No.13

Persamaan garis 3y – 2x + 18 = 0, maka gradiennya adalah …

PEMBAHASAN :
Persamaan garis ubah ke bentuk y = mx + c, sehingga diperoleh:
3y – 2x + 18 = 0
3y = 2x – 18

Jawaban A

Soal No.14

Koordinat yang dilalui oleh persamaan garis y = 15 – 3x, kecuali …

1. (1,12)
2. (3,6)
3. (4,2)
4. (2,9)

PEMBAHASAN :
Untuk menyelesaikan soal di atas adalah dengan menguji pilihan satu persatu, sebagai berikut:

1. Koordinat (1,12)
   x = 1
   y = 15 – 3x
   y = 15 – 3(1)
   y = 12
   (1,12) (dilalui)
2. Koordinat (3,6)
   x = 3
   y = 15 – 3x
   y = 15 – 3(3)
   y = 6
   (3,6) (dilalui)
3. Koordinat (4,2)
   x = 4
   y = 15 – 3x
   y = 15 – 3(4)
   y = 3
   (4,3) (tidak dilalui)
4. Koordinat (2,9)
   x = 2
   y = 15 – 3x
   y = 15 – 3(2)
   y = 9
   (2,9) (dilalui)

Jawaban C

Soal No.15

Persamaan di bawah ini yang memiliki gradien (m) = 4/3 adalah …

1. 6x – 2y + 4 = 0
2. 4x – 3y + 6 = 0
3. 8y + 6x – 12 = 0
4. 3y + 4x – 6 = 0

PEMBAHASAN :
Untuk mengetahui persamaan garis dengan gradien (m) = 4/3 adalah dengan mengubah persamaan menjadi y = mx + c dan mengujinya satu persatu sebagai berikut:

1. 6x – 2y + 4 = 0
   6x + 4 = 2y
   y = 3x + 2
   m = 3
2. 4x – 3y + 6 = 0
   4x + 6 = 3y
   
3. 8y + 6x – 12 = 0
   8y = – 6x + 12
   4y = – 3x + 6
   
4. 3y + 4x – 6 = 0
   3y = – 4x + 6
   

Maka jawaban yang tepat adalah jawaban pilihan B
Jawaban B

Soal No.16

Titik – titik di bawah ini membentuk garis sejajar dengan sumbu x adalah …

1. (-1,-4) dan (1,4)
2. (1,3) dan (3,1)
3. (2,3) dan (2,-5)
4. (1,5) dan (3,5)

PEMBAHASAN :
Apabila terdapat garis yang sejajar dengan sumbu x, maka gradiennya adalah nol (m = 0), maka berlaku rumus sebagai berikut:

1. (-1,-4) dan (1,4)
   
2. (1,3) dan (3,1)
   
3. (2,3) dan (2,-5)
   
4. (1,5) dan (3,5)
   

Maka jawaban yang tepat adalah jawaban pilihan D
Jawaban D

Soal No.17

Dua buah garis, garis A dan garis B saling tegak lurus. Gradien garis A = -2 sedangkan gradien garis B adalah …

1. ½
2. 2
3. -1
4. 1

PEMBAHASAN :
Hasil kali gradien dari dua garis yang saling tegak lurus = -1
Maka gradien garis B dapat dihitung sebagai berikut:
m_A x m_B = -1
-2 x m_B = -1

Jawaban A

Soal No.18

Garis y = 5 memiliki gradien …

1. -1
3. Tidak memiliki gradien
4. 1

PEMBAHASAN :
Apabila suatu garis sejajar dengan sumbu y maka garis tersebut tidak memiliki gradien. Garis y = 5 sejajar sumbu y.
Jawaban C

Soal No.19

Garis lurus yang melalui titik (2,1) dan titik (3,-5) memiliki gradien …

1. 1
2. -3
4. -6

PEMBAHASAN :
Gradien  yang melalui dua titik, titik (2,1) dan titik (3,-5)  maka rumus  gradien yang berlaku sebagai berikut:

Jawaban D

Soal No.20

Garis A dan B saling tegak lurus, garis B memiliki persamaan 3y + 6x – 12 = 0 sedangkan garis A melewati titik (2,3). Maka persamaan garis A adalah …

1. 2y – 3x + 6 = 0
2. 2y – x – 4 = 0
3. 2y + x – 10 = 0
4. y – 6x – 5 = 0

PEMBAHASAN :
Menentukan gradien garis B:
3y + 6x – 12 = 0
⇔ 3y = – 6x + 12
⇔ y = – 2x + 4

Maka gradien garis B = – 2
Hasil kali gradien dari dua garis yang saling tegak lurus = -1
Maka gradien garis A dapat dihitung sebagai berikut:
m_A x m_B = -1
m_A x -2 = – 1
m_A = ½

Untuk persamaan garis A yang melewati titik (2,3) berlaku  rumus sebagai berikut:
y – y₁ = m (x – x₁ )
y – (3) = ½ (x – 2)
y – 3 = ½ x – 1
y = ½ x + 2
dikalikan 2, menjadi:
2y – x – 4 = 0
Jawaban B

Soal No.21

Diketahui persamaan garis y = 4x + 9 dan melalui titik (2,-5). Persamaan garis yang sejajar dengan persamaan tersebut adalah …

1. y = 4x – 13
2. y = 2x + 5
3. y = 6x – 5
4. y = 3x – 2

PEMBAHASAN :
Dua garis yang sejajar memiliki gradien yang sama:
Persamaan garis :
y = 4x + 9
m = 4

Untuk persamaan garis yang melewati titik (2,-5)dengan m = 4 berlaku  rumus sebagai berikut:
y – y₁ = m (x – x₁ )
y – (- 5) = 4 (x – 2)
y + 5 = 4x – 8
y = 4x – 13
Jawaban A

Soal No.22

Suatu persamaan garis yang melalui titik (1,2) dan (3, -4) adalah …

1. y = 2x + 5
2. y = – 5x +3
3. y = -3x + 5
4. y = x + 13

PEMBAHASAN :
Persamaan garis lurus melalui dua titik yaitu (1,2) dan (3, -4). Apabila diketahui dua titik koordinatnya. Rumus yang berlaku  adalah sebagai berikut:

Jawaban C

Soal No.23

Gradien garis yang tegak lurus dengan garis 2y = 6x + 10 adalah …

1. – 1/3
2. 1/2
3. -1
4. 2/3

PEMBAHASAN :
Hasil kali gradien dari dua garis yang saling tegak lurus = -1
2y = 6x + 10
Dibagi 2
y = 3x + 5
m₁ = 3

Maka gradien garis yang saling tegak lurus tersebut  dapat dihitung sebagai berikut:
m₁ x m₂ = -1
3 x m₂ = -1
m₂= – 1/3
Jawaban A

Soal No.24

Persamaan garis lurus yang melewati titik (2,5) dan (-2, 1) adalah …

1. y = 2x
2. y = x + 3
3. y = 2x – 5
4. y = – 3x – 2

PEMBAHASAN :
Persamaan garis lurus melalui dua titik yaitu (2,5) dan (-2, 1). Apabila diketahui dua titik koordinatnya. Rumus yang berlaku  adalah sebagai berikut:

Jawaban B

Soal No.25

Gradien garis yang melalui titik (-4,3) dan (2,4) adalah …

1. 1/3
2. – 1/2
3. 1/6
4. -1

PEMBAHASAN :
Gradien  yang melalui dua titik  (-4,3) dan (2,4) maka rumus  gradien yang berlaku sebagai berikut:

Jawaban C

Soal No.26

Diketahui garis 3x + 8y = 15 dan 2x + 6y = 8, maka koordinat titik potongnya adalah …

1. (13,-3)
2. ( ½ , -2)
3. (2,5)
4. (-3, 4)

PEMBAHASAN :
Menyelesaikan sistem persamaan linier dua variable untuk mencari titik potong, sebagai berikut:
3x + 8y = 15  |x 2 → 6x + 16y = 30
2x + 6y = 8    |x 3 → 6x + 18y = 24
.                                              -2y = 6
.                                                  y = -3

Sehingga nilai x dapat dicari sebagai berikut:
3x + 8y = 15
3x + 8(-3) = 15
3x – 24 = 15
3x = 39
x = 13

Maka titik potong untuk kedua garis tersebut adalah (13,-3)
Jawaban A

Soal No.27

Diketahui persamaan garis yang melalui titik (0,5) dan (2,3) adalah …

1. 2y – 3x + 12 = 0
2. – 3y + 5x + 10 = 0
3. y – 2x – 4 = 0
4. y + x – 5 = 0

PEMBAHASAN :
Persamaan garis lurus melalui dua titik yaitu (0,5) dan (2, 3), apabila diketahui dua titik koordinatnya. Rumus yang berlaku  adalah sebagai berikut:

2(y – 5) = -2x
2y – 10 = -2x
2y + 2x – 10 = 0
y + x – 5 = 0
Jawaban D

Soal No.28

Garis dengan gradien = 3 dan melewati titik (- 2,1). Maka persamaan garis tersebut adalah …

1. y = 3x + 7
2. y = – 2x + 5
3. y = 4x – 3
4. y = x + 1

PEMBAHASAN :
Persamaan garis lurus melalui titik (-2 ,1 ) dan bergradien m = 3. Apabila diketahui gradien dan salah satu titik kordinatnya. Rumus yang berlaku  adalah sebagai berikut:
y – y₁ = m (x – x₁ )
y – 1 = 3 (x – ( – 2))
y – 1 = 3 (x + 2)
y – 1 = 3x + 6
y = 3x + 7
Jawaban A

Soal No.29

Terdapat sebuah garis 3y + 6x – 12 = 0, maka persamaan garis yang sejajar dengan garis tersebut adalah …

1. 3y – 2x + 6 = 0
2. y = ½ x – 3
3. – 2x – y + 7 = 0
4. y = 5 + 3x

PEMBAHASAN :
Dua garis yang sejajar memiliki gradien yang sama (m₁ = m₂ )
Gradien garis 3y + 6x – 12 = 0 adalah:
3y = – 6x + 12
y = – 2x + 4
Maka gradiennya (m) = – 2

Mencari gradien yang sama dengan menguji pilihan satu persatu:

1. 3y – 2x + 6 = 0
   3y = 2x – 6
   
2. y = ½ x – 3
   m = ½
3. – 2x – y + 7 = 0
   y = – 2x + 7
   m = – 2
4. y = 5 + 3x
   m = 3

Jawaban C

Soal No.30

Gradien garis A = p dan gradien garis B = q = ½ . Garis-garis tersebut saling tegak lurus, maka nilai p adalah …

1. – 1
2. – ½
3. – 2
4. ½

PEMBAHASAN :
Hasil kali gradien dari dua garis yang saling tegak lurus adalah – 1 (m_A x m_B = – 1)
p x q = – 1
p x ½ = – 1
p = – 2
Jawaban C

Soal No.31

Sebuah garis 3y = – 9x + 3 besar gradiennya adalah …

1. ½
2. – 1
3. – 3
4. – 9

PEMBAHASAN :
Gradien adalah koefisien dari variable x, maka persamaan garis harus diubah terlebih dahulu kebentuk y = mx + c
3y = – 9x + 3       Dibagi 3
y = – 3x + 1
Sehingga gradiennya (m) = – 3
Jawaban C

Soal No.32

Garis x = 3 maka gradien garisnya adalah …

2. Tidak memiliki gradien
3. 1
4. -1

PEMBAHASAN :
x = 3 (garis sejajar sumbu y)
Apabila suatu garis sejajar dengan sumbu y maka garis tersebut tidak memiliki gradien
Jawaban B

Soal No.33

Perhatikan gambar di bawah ini!

Persamaan garis tersebut adalah …

1. y = 5
2. y = – 5
3. x = 5
4. x = -5

PEMBAHASAN :
Garis di atas terbentuk dari titik-titik yang terletaj pada x = 5. Sehingga persamaan garisnya adalah x = 5.
Jawaban C

Soal No.34

Di bawah ini terdapat garis pada sebuah grafik

Persamaan garis tersebut adalah …

1. y + 3x – 7 = 0
2. 2y – 3x – 5 = 0
3. 3y – 4x – 1 = 0
4. y + 2x + 3 = 0

PEMBAHASAN :
Persamaan garis lurus melalui dua titik yaitu (2,3 ) dan (5,7 ). Apabila diketahui dua titik kordinatnya. Rumus yang berlaku  adalah sebagai berikut:

Jawaban C

Soal No.35

Garis di bawah ini yang melalui titik (2,1) adalah …

1. 2y + 3x = 10
2. 3y – 4x = 12
3. 3y + 5x = 13
4. y + 2x = 6

PEMBAHASAN :
Untuk mengetahui garis yang melalui titik (2,1) harus dilakukan pengujian pada setiap pilihan sebagai berikut:

1. 2y + 3x = 10
   2(1) + 3(2) = 10
   2 + 6 ≠ 10
2. 3y – 4x = 12
   3(1) – 4(2) = 12
   3 – 8 ≠ 12
3. 3y + 5x = 13
   3(1) + 5(2) = 13
   3 + 10 = 13
   13 = 13
4. y + 2x = 6
   1 + 2(2) = 6
   1 + 4 = 6
   5 ≠ 6

Maka jawaban yang adalah C
Jawaban C

Soal No.36

Suatu titik (a,4) dilalui oleh garis 3x – 4y = 14. Maka nilai a adalah …

1. 12
2. – 8
3. 14
4. 10

PEMBAHASAN :
Titik (a,4) → (x,y)
3x – 4y = 14
⇔ 3(a) – 4(4) = 14
⇔ 3a – 16 = 14
⇔ 3a = 30
⇔ a = 10
Jawaban D

Soal No.37

Garis y – 8 = 0 adalah garis …

1. Melalui titik (0,0)
2. Sejajar sumbu y
3. Sejajar sumbu x
4. Lengkung terbuka ke atas

PEMBAHASAN :
y – 8 = 0
y = 8
garis tersebut adalah garis yang sejajar sumbu x
Jawaban C

Soal No.38

Sebuah garis dengan persamaan ½ py = (3p – 2)x, memiliki gradien = 3. Maka nilai 3p – 1 adalah …

2. 1
3. 2
4. 3

PEMBAHASAN :
½ py = (3p – 2)x, ubah ke persamaan y = mx + c

Maka nilai 3p – 1 adalah:

Jawaban D

Soal No.39

Garis x = 1 memotong garis 2x + 5y + 13 = 0 di titik P. Persamaan garis yang melalui titik P dan sejajar sumbu X adalah …

1. y = -3
2. y = 2
3. y = – ½
4. y = 1

PEMBAHASAN :
Menentukan titik P:
x = 1
2x + 5y + 13 = 0
2(1) + 5y + 13 = 0
5y + 15 = 0
5y = – 15
y = – 3
Titik P = (1,- 3)

Sehingga garis yang sejajar sumbu X dan melalui titik P adalah garis y = -3
Jawaban A

Soal No.40

Pernyataan yang sesuai dengan persamaan garis y = 2x – 5 kecuali …

1. Melalui titik (1,-3)
2. Melalui titik (2,-1)
3. Tidak melalui titik (0,0)
4. Memotong sumbu x di (5/2, 0)

PEMBAHASAN :

Diuji ke setiap pilihan jawaban:

1. Melalui titik (1,-3)
   x = 1
   y = 2x – 5
   y = 2(1) – 5
   y = -3
   Melalui titik (1,-3)
2. Melalui titik (2,-2)
   x = 2
   y = 2x – 5
   y = 2(2) – 5
   y = -1
   tidak melalui titik (2,-2)
3. Tidak melalui titik (0,0)
   x = 0
   y = 2x – 5
   y = 2(0) – 5
   y = – 5
   tidak melalui titik (0,0)
4. Memotong sumbu x di (5/2, 0)
   y = 0
   y = 2x – 5
   2x – 5 = 0
   2x = 5
   x = 5/2
   memotong sumbu x di (5/2, 0)

Jawaban B