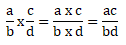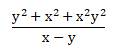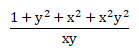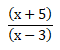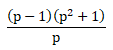Rangkuman Materi, Contoh Soal & Pembahasan Persamaan & Fungsi Kuadrat SMP

By Posted on

Untuk Pembelajaran selanjutnya…

Bentuk Aljabar

Bentuk aljabar merupakan suatu bentuk matematika untuk menyelesaikan masalah yang dalam penyajiannya memuat huruf-huruf untuk mewakili bilangan yang belum diketahui. Unsur-unsur aljabar meliputi:

  1. Variable/ peubah: lambang untuk mengganti suatu bilangan yang belum diketahui nilai pastinya. Misalnya dengan huruf kecil a, b, c, x, y, dst.
  2. Koefisien: konstanta dari suatu suku pada bentuk aljabar. Contoh: 3x2 – 7x + 2, 7 = koefisien x.
  3. Konstanta: suku dari suatu bentuk aljabar dalam bentuk bilangan yang tidak memuat variable. Contoh: 5 + 6x2 – x, 5 = konstanta
  4. Faktor: bilangan yang membagi habis suatu bilangan (bilangan pembagi habis)
  5. Suku dalam bentuk aljabar adalah suatu variable beserta koefisien atau konstanta yang dipisahkan oleh operasi hitung. Suku dalam aljabar dibagi menjadi dua, yaitu:
    • Suku sejenis: suku dengan variable serta pangkat yang sama pada masing-masing variabelnya.
    • Suku tidak sejenis: suku dengan variable serta pangkat yang berbeda pada masing-masing variabelnya.

    Berdasarkan banyaknya penggunaan operasi hitung, suku dibagi menjadi:

    • Suku satu: bentuk aljabar yang tidak dihubungkan oleh operasi hitung. Contoh: 5x atau 2ab atau -7xy
    • Suku dua: bentuk aljabar yang dihubungkan oleh satu operasi hitung. Contoh: 4x+5 atau 2a-6
    • Suku tiga: bentuk aljabar yang dihubungkan oleh dua operasi hitung. Contoh: 3x+2y-xy

Operasi Hitung Pada Bentuk Aljabar

  1. Penjumlahan dan pengurangan: penjumlahan dan pengurangan pada bentuk aljabar hanya bisa dilakukan pada suku-suku yang sejenis atau sama.
  2. Perkalian: perkalian bilangan bulat pada bentuk aljabar akan berlaku sifat distributive (penyebaran) terhadap penjumlahan dan pengurangan.
  3. Perpangkatan: perkalian yang berulang pada bilangan yang sama. Hal ini berlaku juga pada bentuk aljabar
  4. Pembagian: menentukan factor persekutuan dari pembilang dan penyebut, kemudian lakukan pembagian pada pembilang dan penyebut masing-masing dengan faktor sekutunya.
  5. Pecahan, syarat yang berlaku:
    • Pada operasi pecahan bentuk aljabar untuk penjumlahan dan pengurangan harus disamakan penyebutnya terlebih dahulu.
    • Perkalian pecahan bentuk aljabar caranya pembilang kali pembilang dan penyebut kali penyebut kemudian sederhanakan apabila bisa disederhanakan, bentuk umumnya sebagai berikut:

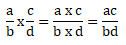
      Dengan b ≠ 0 dan d ≠ 0
    • Pembagian pecahan bentuk aljabar caranya dengan mengubah ke bentuk perkalian dengan membalik pecahan pembaginya, pembilang jadi penyebut dan penyebut jadi pembilang. Bentuk umumnya sebagai berikut:

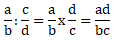
      Dengan b ≠ 0, c ≠ 0, dan d ≠ 0

Faktorisasi Bentuk Aljabar

Faktorisasi bentuk aljabar adalah mengubah bentuk penjumlahan menjadi suatu bentuk perkalian dari bentuk aljabar. Jenis-jenis faktorisasi bentuk aljabar, sebagai berikut:

  1. Menggunakan sifat distributif
    ap + aq → a(p + q), dengan a merupakan faktor persekutuan dari ap dan aq
  1. Selisih dua kuadrat
    (a + b)(a – b) → (a + b)(a – b) = a2 – ab + ab – b2 = a2 – b2
    a2 – b2 = (a + b)(a – b)
    maka, a2 – b2 adalah selisih dua kuadrat
  1. Bentuk kuadrat:
    1. ax2 + bx + c, a = 1fa
      x2 + (p+q)x + pq = ax2 + bx + c
      a = 1, b = p + q, c = pq
      faktornya (x + p) (x + q)
      p dan q adalah faktor c
    2. ax2 + bx + c, a ≠ 1 dan a ≠ 0
      ax2 + bx + c = ax2 + px + qx + c
      dengan p x q = a x c dan p + q = b
      atau ax2 + bx + c = 1/a (ax + m)(ax + n)
      m x n = a x c dan m + n = ba

Soal No.1

Selesaikan persamaan kuadrat berikut menggunakan faktorisasi

  1. x2 +2x – 3 = 0
  2. 3x2 = 5x + 2
  3. 2x2 + 6x = 0

PEMBAHASAN :

  1. x2 + 2x – 3 = 0
    (x-1)(x+3) = 0
    x-1 = 0 atau x + 3 = 0
    x = 1 atau x = -3
  2. 3x2 = 5x + 2
    3x2 – 5x -2 = 0
    (3x+1)(x-2) = 0
    3x + 1 = 0 atau x – 2 = 0
    x = – 1/3 atau x = 2
  3. 2x2 + 6x = 0
    2x(x + 3) = 0
    2x = 0 atau x + 3 = 0
    x = 0 atau x = -3

Soal No.2

Tentukan himpunan penyelesaian dari 9x2 – 4 = 0

PEMBAHASAN :
9x2 – 4 = 0
(3x – 2)(3x + 2) = 0
3x – 2 = 0 atau 3x + 2 = 0
x = atau x =
Maka himpunan penyelesaiannya adalah

Soal No.3

Tentukan himpunan penyelesaian dari x2 + 6x – 16 = 0 dengan cara melengkapkan kuadrat sempurna

PEMBAHASAN :
Cara melengkapkan kuadrat sempurna, langkah-langkahnya:

  1. Letakan suku-suku yang mengandung peubah (variabel) di ruas kiri sedangkan konstanta di ruas kanan
    x2 + 6x – 16 = 0
    x2 + 6x = 16
  2. Koefisien x2 nya harus satu, dalam persamaan tersebut koefisien x2 sudah 1.
  3. Tambahkan kedua ruas dengan kuadrat dari setengah koefisen x

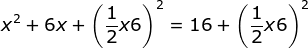
    x2 + 6x + 32 = 16 + 32
    (x + 3)2 = 25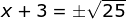

    x + 3 = ± 5
    x + 3 = 5 atau x + 3 = -5
    x = 2 atau x = -8

Soal No.4
Tentukan himpunan penyelesaian dari 2x2 + 9x -5 = 0 dengan menggunakan metode rumus!

PEMBAHASAN :
Dari persamaan 2x2 + 9x -5 = 0 diperoleh informasi:
a = 2, b = 9, c = -5.
Menentukan himpunan penyelesaiannya menggunakan rumus:




Maka himpunan penyelesaiannya adalah {-5, ½}

Soal No.5

Himpunan penyelesaian dari 3x2 – 4x = 5 adalah…

PEMBAHASAN :
3x2 – 4x = 5
3x2 – 4x – 5 = 0
Maka :
a = 3, b = -4, dan c = -5, sehingga himpunan penyelesaiannya:




Maka himpunan penyelesaiannya =

Soal No.6

Himpunan penyelesaian dari  adalah…

PEMBAHASAN :

Persamaan dikali 4 agar tidak dalam bentuk pecahan
     x  4
⇔6x2– 7x – 3 = 0
⇔ (2x – 3)(3x + 1) = 0
⇔ 2x – 3 = 0 atau 3x + 1 = 0

Maka himpunan penyelesaiannya adalah

Soal No.7

Himpunan penyelesaian dari adalah…

PEMBAHASAN :
       dikali x

⇔ x2 + 4 = 4 + 3x
⇔ x2 + 4 – 3x – 4 = 0
⇔ x2 – 3x = 0
⇔ x(x – 3) = 0
⇔ x = 0 atau x = 3
x = 0 tidak memenuhi karena jika dimasukan hasilnya tidak didefinisikan. Maka himpunan penyelesaiannya {3}

Soal No.8

Tentukan persamaan kuadrat yang akar-akarnya diketahui sebagai berikut!

  1. 2 dan 3
  2. -5 dan 1

PEMBAHASAN :

  1. Diketahui:
    x1 = 2 dan x2 = 3
    (x – x1)(x – x2) = 0
    (x – 2)(x – 3) = 0
    x2 – 5x + 6 = 0
  2. Diketahui:
    x1 = -5 dan x2 = 1
    (x – x1)(x – x2) = 0
    (x – (-5))(x – 1) = 0
    (x + 5)(x – 1) = 0
    x2 + 4x – 5 = 0
  3. Diketahui:
    x1 = dan x2 =
    (x – x1)(x – x2) = 0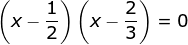



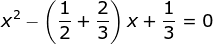
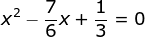
    6x2 – 4x – 5 = 0
  4. Diketahui:
    x1 =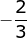  dan x2 =
    (x – x1)(x – x2) = 0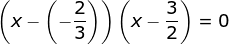




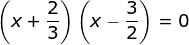
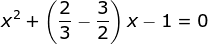
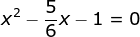
    6x2 – 5x – 6 = 0

Soal No.9

Tentukan persamaan kuadrat yang akar-akarnya diketahui dengan menggunakan rumus jumlah dan hasil kali akar-akar

  1. 2 dan 3
  3. -5 dan 1

PEMBAHASAN 

  1. Diketahui:
    x1 = 2 dan x2 = 3
    x1 + x2 = 2 + 3 = 5
    x1 . x2 = (2)(3) = 6
    Maka:
    x2 – (x1 + x2)x + x1.x2 = 0
    x2 – 5x + 6 = 0
  2. Diketahui:
    x1 = -5 dan x2 = 1
    x1 + x2 = -5 + 1 = -4
    x1 . x2 = (-5)(1) = -5
    Maka:
    x2 – (x1 + x2)x + x1.x2 = 0
    x2 – (-4)x + (-5) = 0
    x2 + 4x – 5 = 0
  3. Diketahui:



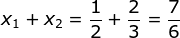
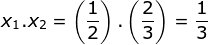
    Maka:
    x2 – (x1 + x2)x + x1.x2 = 0
    x2 – x + = 0
    6x2 – 7x + 2 = 0
  4. Diketahui:



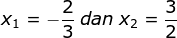
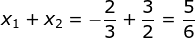
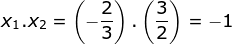
    Maka:
    x2 – (x1 + x2)x + x1.x2 = 0
    x2 –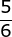 x – 1 = 0
    6x2 – 5x – 6 = 0

Soal No.10

Keliling sebidang tanah yang berbentuk persegi panjang adalah 70 m dan luasnya 300 m2. Tentukan panjang dan lebar persegi panjang tersebut!

PEMBAHASAN :
Jika dimisalkan:
lebar = x m
karena keliling 70 m dimana keliling = 2p + 2l = 2(p+l) = 70 m
maka p + l = 70/2 = 35 m
sehingga p = 35 – l = 35 – x m
Maka untuk menentukan x dapat diperoleh dari rumus luas
L = p x l = (35 – x).x = 300 m2
35x – x2 = 300
x2 + 35x – 300 = 0
(x – 15)(x – 20) = 0
x – 15 = 0 atau x – 20 = 0
x = 15 atau x = 20
sehinggal lebar = x m = 15 m (diambil yang lebih kecil karena lebih lebih pendek dibanding panjang)
dan panjangnya = 35 – 15 m = 20 m

Soal No.11

5x2 + 2x – 8, koefisien x pada bentuk aljabar tersebut adalah …

  1. 2
  2. 5
  3. 6
  4. 8

PEMBAHASAN :
5x2 + 2x – 8
Pada bentuk aljabar di atas koefisien x adalah 2
Jawaban A

Soal No.12

Hasil dari perhitungan 3p + 2q dengan p = 2x + 3y – 5 dan q = 6x – 4y + 8 adalah …

  1. 18x – y + 1
  2. 18x + y + 1
  3. – 18x – y – 1
  4. 18x + y – 1

PEMBAHASAN :
Diketahui:
p = 2x + 3y – 5
q = 6x – 4y + 8

Maka 3p + 2q dapat dihitung sebagai berikut:

3p + 2q = 3(2x + 3y – 5) + 2(6x – 4y + 8)
.              = 6x + 9y – 15 + 12x – 8y + 16
.              = 18x + y + 1
Jawaban B

Soal No.13

Apabila a = 4p – q – 3 dan b = 3p + 5q + 6 maka 2a + 3b adalah …

  1. 17p – 13q – 12
  2. 17p + 13q + 12
  3. – 17p – 13q + 12
  4. 17p + 13q – 12

PEMBAHASAN :
Diketahui:
a = 4p – q – 3
b = 3p + 5q + 6

Maka
2a + 3b = 2(4p – q – 3) + 3(3p + 5q + 6)
.              = 8p – 2q – 6 + 9p + 15q + 18
.              = 17p + 13q + 12
Jawaban B

Soal No.14

Hasil dari (2pq2 + 3qr)(pq – 5r) adalah …

  1. – 2p2 q3 – 7pq2 r – 15qr2
  2. 2p2 q3 + 7pq2 r – 15qr2
  3. 2p2 q3 + 7pq2 r + 15qr2
  4. 2p2 q3 – 7pq2 r – 15qr2

PEMBAHASAN :
(2pq2 + 3qr)(pq – 5r)
⇔ 2pq2 (pq – 5r) + 3qr (pq – 5r)
⇔ 2p2 q3 – 10pq2 r + 3pq2 r – 15qr2
⇔ 2p2 q3 – 7pq2 r – 15qr2
Jawaban D

Soal No.15

Hasil dari

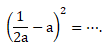
PEMBAHASAN :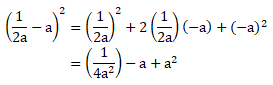

Jawaban C

Soal No.16

Di bawah ini bentuk aljabar bersuku tiga adalah …

  1. 2x + 5y
  2. 3x – 6y + 5
  3. 7xy – 4
  4. x2 – 2xy + 3y2 – 5z

PEMBAHASAN :

  • 2x + 5y (bentuk aljabar bersuku dua)
  • 3x – 6y + 5 (bentuk aljabar bersuku tiga)
  • 7xy-4 (bentuk aljabar bersuku 2)
  • x2 – 2xy + 3y2 – 5z (bentuk aljabar bersuku empat)

Jawaban B

Soal No.17

Bentuk aljabar suku sejenis di bawah ini adalah …

  1. x3  dan y3
  2. 2x2 y dan 2xy2
  3. 3x2 y2 dan 2x2 y2
  4. x3 y2 dan 5x2 y3

PEMBAHASAN :
Suku dalam aljabar dibagi menjadi dua, yaitu:

  • Suku sejenis: suku dengan variable serta pangkat yang sama pada masing-masing variabelnya.
  • Suku tidak sejenis: suku dengan variable serta pangkat yang berbeda pada masing-masing variabelnya.

Jawaban C

Soal No.18

Pengurangan dari bentuk aljabar 6x2 + 3x – 8 dan 4x2 – 2x + 5 adalah …

  1. – 2x2 + 5x – 13
  2. 2x2 –  5x – 13
  3. 2x2 + 5x + 13
  4. 2x2 + 5x – 13

PEMBAHASAN :
(6x2 + 3x – 8) – (4x2 – 2x + 5)
⇔ 6x2 + 3x – 8 – 4x2 + 2x – 5
⇔ 2x2 + 5x – 13
Jawaban D

Soal No.19

Hasil dari (2x + 1)(3x – 5)= …

  1. 6x2 – 7x – 5
  2. 6x2 + 7x – 5
  3. 6x2 – 7x + 5
  4. – 6x2 – 7x – 5

PEMBAHASAN :
(2x + 1)(3x – 5)
⇔ 2x(3x – 5) + 1(3x – 5)
⇔ 6x2 – 10x + 3x – 5
⇔ 6x2 – 7x – 5
Jawaban A

Soal No.20

Sederhanakan pecahan bentuk aljabar dari

PEMBAHASAN :
Pembagian pecahan bentuk aljabar caranya  dengan mengubah ke bentuk perkalian dengan membalik pecahan pembaginya, pembilang jadi penyebut dan penyebut jadi pembilang.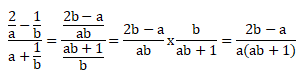

Jawaban B

Soal No.21

Hasil dari

PEMBAHASAN :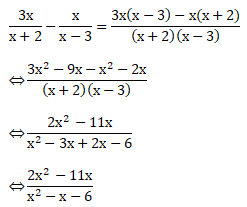

Jawaban B

Soal No.22

Perhatikan persamaan kuadrat berikut ini!

Maka nilai a + b = …

  2. 1
  3. 2
  4. 3

PEMBAHASAN :

Dari persamaan di atas didapat nilai a = 1 dan b = 2
Maka a + b = 1 + 2 = 3
Jawaban D

Soal No.23

Hasil perhitungan dari

adalah…

PEMBAHASAN :

Jawaban C

Soal No.24

Jika (2x +3y)(px + qy) = rx2 +23xy + 12y2 maka nilai r adalah …

  1. 3
  2. 4
  3. 10
  4. 15

PEMBAHASAN :
(2x +3y)(px + qy) = 2x(px + qy) + 3y(px + qy) = 2px2 + 2xqy + 3ypx + 3qy2
⇔ 2px2 + 2xqy + 3ypx + 3qy2 = rx2 +23xy + 12y2
⇔ 2px2 + (2xqy + 3ypx) + (3q)y2 = rx2 +23xy + 12y2

Menentukan nilai q
2p = r
3q = 12
q = 4

Menentukan nilai p
2xqy + 3ypx = 23xy
⇔ 2q + 3p = 23
⇔ 2(4) + 3p = 23
⇔ 3p = 15
⇔ p = 5

Menentukan nilai r
2p = r
r = 2 x 5 = 10
Jawaban C

Soal No.25

Hasil perhitungan dari

PEMBAHASAN :

Jawaban C

Soal No.26

Hasil dari (2p + 5q)2 – (3p – q)2 = …

  1. 5p2 + 14pq + 26q2
  2. – 5p2 + 14pq + 26q2
  3. – 5p2 – 14pq – 26q2
  4. 5p2 + 14pq – 26q2

PEMBAHASAN :
(2p + 5q)2 – (3p – q)2 = {(2p)2 + 2(2p)(5q) + (5q)2 } – {(3p)2 + 2(3p)(- q) + (-q)2
⇔ 4p2 + 20pq + 25q2 – 9p2 – 6pq + q2
⇔ – 5p2 + 14pq + 26q2
Jawaban B

Soal No.27

Hasil dari

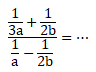
PEMBAHASAN :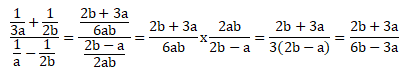

Jawaban A

Soal No.28

Menentukan (x3 y2 z4 )2 adalah …

  1. x5 y4 z6
  2. x6 y4 z8
  3. x2 y2 z2
  4. x z2

PEMBAHASAN :
Operasi hitung pada pangkat sebagai berikut:
(pa )b = paxb
Maka (x3 y2 z4 )2 = x3×2 y2×2 z4×2 = x6 y4 z8
Jawaban B

Soal No.29

Hasil perhitungan dari (2x + 5)(5x – 7) = …

  1. 10x2 + 11x – 35
  2. x2 + 10x – 35
  3. 10x2 – 11x – 35
  4. 10x2 + 11x – 15

PEMBAHASAN :
(2x + 5)(5x – 7) = 2x(5x – 7) + 5(5x – 7)
⇔ 2x (5x) + 2x(-7) + 5(5x) + 5(-7)
⇔ 10x2 – 14x + 25x – 35
⇔ 10x2 + 11x – 35
Jawaban A

Soal No.30

Hasil perhitungan dari (2x + 3)(5x + 2) = px2 + qx + 6. Nilai p + q = …

  1. -9
  2. -10
  3. -11
  4. -12

PEMBAHASAN :
(2x + 3)(5x + 2) = 2x(5x + 2) + 3(5x+2) = 10x2 + 4x + 15x + 6 = 10x2 + 19x + 6
⇔ 10x2 + 19x +96 = px2 –  qx – 6
⇔ p = 10 , q = 19
Maka nilai p – q = 10 – 19 = -9
Jawaban A

Soal No.31

Bentuk sederhana dari bentuk  aljabar 4a2 b2 + 24a2 b adalah …

  1. 4a2 b(b + 6)
  2. 4a b(b – 6)
  3. 4a2 b2(b + 6)
  4. 4a2 b2(b – 6)

PEMBAHASAN :
Menentukan faktor persekutuan terbesar (FPB) dari 4a2 b2 – 24a2 b yaitu 4a2 b
Maka bentuk sederhana dari 4a2 b2 + 24a2b = 4a2 b(b + 6)
Jawaban A

Soal No.32

Pemfaktoran dari p(x – y) + q(x – y) adalah …

  1. (a – y)(x + q)
  2. (x – y)(p + q)
  3. (x + y)(p – q)
  4. (p – q)(x + y)

PEMBAHASAN :
Faktor dari p(x – y) + q(x – y) = (x – y)
Maka pemfaktoran dari p(x – y) + q(x – y) = (x – y)(p + q)
Jawaban B

Soal No.33

Hasil perhitungan dari adalah …

PEMBAHASAN :
Menentukan faktor dari x2 – 16 = (x + 4)(x – 4)
Maka: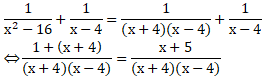

Jawaban B

Soal No.34

Hasil dari menyederhanakan persamaan adalah …

PEMBAHASAN :

Jawaban C

Soal No.35

Hasil sederhana dari  adalah …

PEMBAHASAN :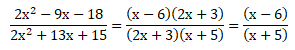

Jawaban C

Soal No.36

Persamaan 8x2 -32 pemfaktorannya adalah …

  1. 8(x + 2)(x – 4)
  2. 8(x – 2)(x – 2)
  3. 4(x + 2)(x – 4)
  4. 8(x + 2)(x – 2)

PEMBAHASAN :
Maka pemfaktoran dari 8x2 -32 = 8(x2 – 4) = 8(x + 2)(x – 2)
Jawaban C

Soal No.37

Persamaan 256x2 – 169y2 pemfaktorannya adalah …

  1. (16x + 13y)(16x – 13y)
  2. (16x – 13y)(16x – 13y)
  3. (- 16x + 13y)(- 16x + 13y)
  4. (16x + 13y)(16x + 13y)

PEMBAHASAN :
Bentuk dasar aljabar x2 – y2 = (x + y)(x – y)
Maka pemfaktoran dari 256x2 – 169y2 = (16x + 13y)(16x – 13y)
Jawaban A

Soal No.38

Hasil perhitungan dari

PEMBAHASAN :

Jawaban D

Soal No.39

Hasil perhitungan dari adalah …

PEMBAHASAN :

Jawaban B

Soal No.40

Pemfaktoran dari persamaan 64x2 – (x – y)2 = …

  1. (7 + y)(9x + y)
  2. (- 7x + y)(- 9x – y)
  3. (7x + y)(x + y)
  4. (7x + y)(9x – y)

PEMBAHASAN :
64x2 – (x – y)2 = {8x – (x – y)}{8x + (x – y)}
⇔ (8x – x + y)(8x + x – y)
⇔ (7x + y)(9x – y)
Jawaban D

Soal No.41

Pemfaktoran dari persamaan ¼ p4 – 2p2 q2 + 4q4 adalah …

  1. (2p + q)(2p – q)(p – 2q)(p + 2q)
  2. ( ½ p + q)( ½ p – q)(p – 2q)(p + 2q)
  3. ( ½ p2 + q)( ½ p2 – q)(p – 2q)(p + 2q)
  4. ( ¼  p + q)( ¼ p – q)(p – 2q)(p + 2q)

PEMBAHASAN :
¼ p4 – 2p2 q2 + 4q4 = ( ½ p2 – q2 )( ½ p2 – q2)
⇔ ½ (p2 – 4q2) ½ (p2 – 4q2)
⇔ ½ (p + 2q)(p – qy) ½ (p + 2q)(p – 2q)
⇔ ( ½ p + q)( ½ p – q)(p – 2q)(p + 2q)
Jawaban B

Soal No.42

Sebuah persegi panjang memiliki luas (x2 – 5x + 4) cm, lebarnya (x – 4) cm, dan panjangnya adalah … cm.

  1. x – 2
  2. x + 3
  3. x – 1
  4. x + 1

PEMBAHASAN :
Diketahui:
Luas = (x2 – 5x + 4) cm
a = 1
b = – 5
c = 4
Lebar = (x – 4) cm
Menentukan x1 dan x2 sebagai berikut:

Menentukan faktor dari persamaan x2 – 5x + 4 = (x – x1 )(x – x2 )
⇔ x – x1 = x – 4
⇔ x – x2 = x – 1
Maka untuk menghitung panjang persegi panjang tersebut, yaitu:
Luas persegi panjang = panjang x lebar

Jawaban C

Soal No.43

Hasil pemfaktoran dari 0,8x2 – 2,4x – 1,8 = …

  1. (0,2x + 0,3)2x – 3)
  2. (0,2x – 0,3)(2x + 3)
  3. 2(0,2x + 0,3)(2x – 3)
  4. 2(0,2x + 0,3)(2x + 3)

PEMBAHASAN :
Diketahui:
a = 0,8
b = – 2,4
c = – 1,8

Maka faktor dari 0,8x2 – 2,4x – 1,8 = (0,4x + 0,6)(2x – 3)
⇔ 2(0,2x + 0,3)(2x – 3)
Jawaban C

Soal No.44

Sebuah segitiga memiliki luas (6x2 – 19x + 15) cm, tingginya (2x – 3) cm, maka panjang alasnya adalah …

  1. 3x – 5
  2. 6x – 10
  3. 2x + 3
  4. 6x + 5

PEMBAHASAN :
Diketahui:
Luas = (6x2 – 19x + 15) cm
Tinggi = (2x – 3) cm

Maka untuk menghitung panjang alasnya, sebagai berikut:
L segitiga = ½  x alas x tinggi
6x2 – 19x + 15 = ½ x alas x 2x – 3
2(6x2 – 19x + 15) = 2x – 3 x alas


Jawaban B

Soal No.45

Hasil perhitungan dari

PEMBAHASAN :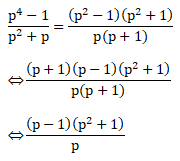

Jawaban B

Soal No.46

PEMBAHASAN :

Jawaban C

Soal No.47

Hasil penyederhanaan dari

PEMBAHASAN :

Jawaban A

Soal No.48

Hasil (p + q)3 adalah …

  1. p3 + 3p2 q2 + 3p2 q2 + q3
  2. p3 –  3p2 q –  3pq2 –  q3
  3. p2 + 3p2 q3  + 3p3 q2 + q2
  4. p3 + 3p2 q + 3pq2 + q3

PEMBAHASAN :
Untuk memudahkan penguraian perpangkatan bentuk aljabar, maka gunakan pola segitiga pascal sebagai berikut:
1
1              1
1              2              1 →  (p + q)2 = p2 + 2pq + q2
1              3              3              1 → (p + q)3 = p3 + 3p2 q + 3pq2 + q3
1              4              6              4              1  →  (p + q)4 = p4 +  4p3 q + 6p2 q2 + 4pq3 + q4
Dst
Jawaban D

Soal No.49

144x2 – px + 100, untuk menyempurnakan persamaan kuadrat tersebut maka nilai p adalah …

  1.  – 44
  2. – 55
  3. – 66
  4. – 77

PEMBAHASAN :
a = 144 →√144 = 12
b = -p
c = 100 → √100 = 10

Maka untuk menentukan nilai p dapat dihitung sebagai berikut:
b = – p = 2 x (12 + 10) = 44
p = -44
Jawaban A

Soal No.50

Hasil perhitungan dari (5x + 3)(3x – 4) adalah …

  1. 5x2 + 11x2 – 12
  2. 15x2 + 11x2 + 12
  3. – 15x2 – x2 – 12
  4. 15x2 – 11x2 – 12

PEMBAHASAN :
(5x + 3)(3x – 4) = 5x(3x – 4) + 3(3x – 4)
⇔ 15x2 – 20x + 9x2 – 12
⇔ 15x2 – 11x2 – 12

Jawaban D

Semoga Bermanfaat

Related posts: