Rangkuman Materi, Contoh Soal & Pembahasan Lingkaran Tingkat SMP

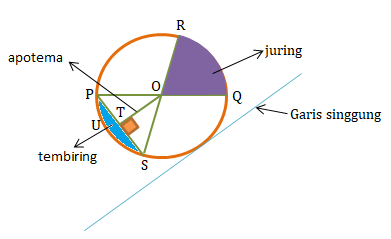
Unsur-Unsur Lingkaran

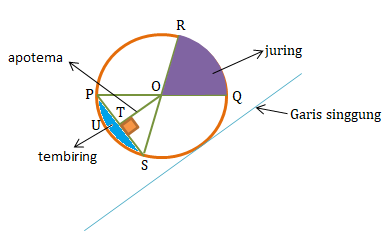
1. Jari-jari lingkaran, adalah garis yang menghubungkan titik pusat lingkaran dengan titik pada keliling lingkaran. Contohnya garis OR, OQ, OP, dan OS.
2. Diameter lingkaran, adalah garis lurus antara dua titik pada keliling lingkaran yang melewati titik pusat lingkaran. Contohnya garis PQ dan garis RS.
3. Titik pusat lingkaran, adalah suatu titik yang berada tepat di tengah-tengah lingkaran. Contohnya titik O.
4. Busur lingkaran, adalah garis lengkung pada keliling lingkaran. Busur lingkaran di bagi 2 macam yaitu:
   • Busur kecil: panjangnya kurang dari setengah lingkaran
   • Busur besar: panjangnya lebih dari setengah lingkaran

   Contohnya: garis PR, RQ, QS, dan PS

5. Tali busur lingkaran, adalah garis lurus yang menghubungkan garis lengkung busur lingkaran pada keliling lingkaran tetapi tidak melewati titik pusat lingkaran. Contohnya garis lengkung PR, RQ, QS, dan PS.
6. Juring lingkaran, adalah daerah yang dibatasi atau diapit oleh dua garis jari-jari dan satu busur lingkaran. Juring lingkaran dibagi menjadi dua yaitu juring kecil dan juring besar tergantung besar kecilnya busur lingkaran. Contohnya daerah QOR.
7. Tembereng lingkaran, adalah daerah yang dibatasi oleh busur lingkaran dan tali busur lingkaran. Contohnya daerah busur PS dan tali busur PS.
8. Sudut lingkaran
   • Sudut pusat lingkaran: sudut antara dua buah jari-jari pada titik pusat lingkaran. Contohnya ∠POQ
   • Sudut keliling lingkaran: sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu pada keliling lingkaran. Contohnya tali busur PR dan RQ bertemu di titik R sehingga membentuk ∠PRQ.

   Sifat-sifat sudut pada lingkaran, sebagai berikut:

   • Apabila sudut keliling suatu lingkaran menghadap diameter lingkaran, maka besar sudut keliling sama dengan 90⁰ .
   • Apabila sudut-sudut keliling menghadap busur yang sama, maka besar sudut-sudut keliling tersebut adalah sama.
   • Jumlah sudut keliling yang saling berhadapan adalah 180⁰ .
9. Garis singgung lingkaran, adalah garis yang memotong lingkaran tepat di satu titik pada keliling lingkaran. Contohnya perhatikan gambar di atas!
10. Apotema lingkaran, adalah garis tegak lurus dengan tali busur merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran. Contohnya garis OU.

Rumus-Rumus Lingkaran

Luas lingkaran

L = π x r² atau L = ¼ π d² k

Keterangan:

π = phi = 3,14 = 22/7

r = jari-jari = ½ x d

d = diameter

Keliling lingkaran

K = 2 x π x r atau K = π x d

Garis singgung

Garis singgung melalui titik di luar lingkaran

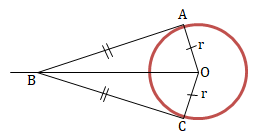
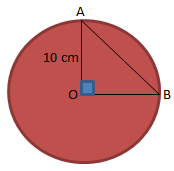
Berlaku teorema Pythagoras:

Perhatikan ΔAOB!

OB² = OA² + AB²

Keterangan:

OA = r = jari-jari

OB = Jarak titik ke pusat lingkaran

AB = panjang garis singgung

Garis singgung dua lingkaran

1. Garis singgung persekutuan luar
   
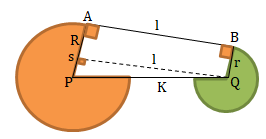
   Berlaku teorema Pythagoras:
   Perhatikan ΔPQS!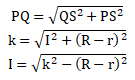
   
   Keterangan:
   R = panjang jari-jari lingkaran besar
   r = panjang jari-jari lingkaran kecil
   k = jarak pusat lingkaran A dan B
   PS = R – r
   I = AB = panjang garis singgung lingkaran A dan B
2. Garis singgung persekutuan dalam
   
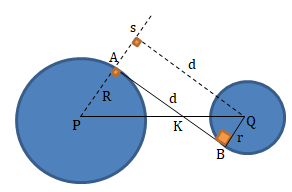
   Perhatikan ΔPQS!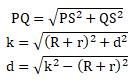
   
   Keterangan:
   AB = d = panjang garis singgung persekutuan dalam
   R = panjang jari-jari lingkaran besar
   r = panjang jari-jari lingkaran kecil
   k = jarak titik pusat kedua lingkaran
   PS = jumlah jari-jari lingkaran P dan Q =  R + r

Lingkaran dalam dan lingkaran luar 

Jari-jari lingkaran luar segitiga:

Jari-jari lingkaran dalam segitiga:

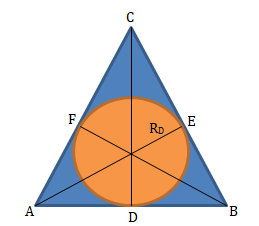
Soal No.1

Jika diketahui keliling suatu lingkaran adalah 78,5 cm. Maka luas lingkaran tersebut adalah… (π = 3,14)

1. 400,00 cm²
2. 454,323 cm²
3. 490,625 cm²
4. 521,425 cm²

PEMBAHASAN :
Diketahui
Keliling = 78,5 cm
Menentukan diameter dari keliling
K = π. d

Menentukan jari-jari dari diameter
d = 2. r
maka r = ½. d = ½. 25 cm = 12,5 cm
Maka luas lingkaran tersebut adalah
L = πr² = 3,14. (12,5)² = 490,625 cm²
Jawaban C

Soal No.2

Diketahui gambar berikut

Luas daerah yang diarsir adalah….

1. 28,26 cm²
2. 33,23 cm²
3. 38,56 cm²
4. 50,16 cm²

PEMBAHASAN :
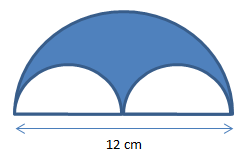
Menentukan luas daerah yang diarsir yaitu dengan mengurangkan luas setengah lingkaran besar dengan 2 luas setengah lingkaran kecil
Luas Arsir = luas setengah lingkaran besar – 2 x luas setengah lingkaran kecil
Menentukan luas setengah lingkaran besar
L = ½ . π. r² = ½ . 3,14. (½.12)² = ½ . 3,14. (6)² = 56,52 cm²
Menentukan luas setengah lingkaran kecil
L = ½ . π. r² = ½ . 3,14. (½.6)² = ½ . 3,14. (3)² = 14,13 cm²
Maka luas daerah yang di arsir adalah
L = 56,52 – 2. 14,13 = 56,52 – 28,26 = 28,26 cm²
Jawaban A

Soal No.3

Jika diketahui panjang busur AB yaitu 9 cm dengan jari-jari lingkaran 8 cm. Maka sudut pusat yang dibentuk oleh busur AB adalah….

1. 50^o
2. 55,5^o
3. 60,5^o
4. 64,5^o

PEMBAHASAN :
Jika digambarkan sebagai berikut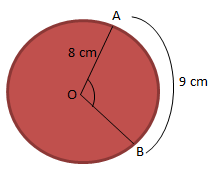

Menentukan ∠AOB dapat ditentukan dari perbandingan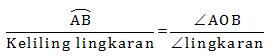




Jawaban D

Soal No.4
Luas juring AOB jika diketahui panjang busur AB yaitu 26,167 cm dan panjang jari-jari lingkarannya yaitu 25 cm adalah….

1. 254,650^o
2. 289,56^o
3. 327,083^o
4. 376,54^o

PEMBAHASAN :
Jika digambarkan sebagai berikut

Menentukan ∠AOB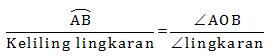



Menentukan luas juring AOB dengan menggunakan perbandingan




Jawaban C

Soal No.5

Jika diketahui lingkaran

Maka luas temberengnya adalah…

1. 20,934 – 50√3 cm²
2. 34,654 – 50√3 cm²
3. 20,934 – 100√3 cm²
4. 34,654 – 100√3 cm²

PEMBAHASAN :
Menentukan luas juring AOB


Menentukan luas Δ AOB

tinggi segitiga diperoleh lewat phytagoras

maka luas Δ AOB
luas Δ AOB = ½. alat. tinggi = ½. 20. 10√3 = 100√3 cm²
Maka luas temberengnya
luas tembereng = luas juring – luas segitiga = 20,934 – 100√3 cm²
Jawaban C

Soal No.6

Diketahui lingkaran berikut

Panjang tali busur AB adalah

1. 8√2
2. 10√2
3. 12√2
4. 15√2

PEMBAHASAN :
Menentukan panjang tali busur abi bisa ditentukan menggunakan Phytagoras pada segitiga AOB

Jawaban B

Soal No.7

Jika Diketahui jari-jari lingkaran P yaitu 12 cm. Panjang garis singgung persekutuan luar lingkaran P dan Q  adalah 6 cm dengan jarak pusat lingkaran nya adalah 10 cm. Maka jari-jari lingkaran Q adalah….

1. 1 cm
2. 2 cm
3. 3 cm
4. 4 cm

PEMBAHASAN :
Diketahui
R = 12 cm
l = 6 cm
k = 10 cm
Menentukan jari-jari dihitung dari rumus persekutuan luar


Kuadratkan kedua sisi
36 = 100 – (144 – 24 r + r²
36 = 100 – 144 + 24r – r²
r² – 24r + 80 = 0
(r – 20) (r – 4) = 0
r = 20 atau r = 4 cm
jari-jari lingkaran B yang mungkin adalah 4 cm
Jawaban D

Soal No.8

Jika dua buah lingkaran dengan Lingkaran P memiliki jari-jari 8 cm dan lingkaran Q = 2 cm. Jika jarak kedua pusat lingkaran adalah 15 cm. Panjang garis singgung persekutuan dalamnya adalah….

PEMBAHASAN :
Diketahui
R = 8 cm
r = 2 cm
k = 15 cm
Menentukan panjang garis singgung persekutuan dalam menggunakan rumus


Jawaban A

Soal No.9

Sebuah taman berbentuk lingkaran berdiameter 24 meter. Di dalam taman itu terdapat sebuah kolam berbentuk persegi panjang berukuran 9 meter x 6 meter. Pada bagian taman di luar kolam ditanami rumput dengan harga Rp. 6.000,00. Bila ongkos pemasangan rumput adalah Rp. 4.000,00 per m² maka biaya penanaman rumput itu seluruhnya adalah….

PEMBAHASAN 
Diketahui
d = 24 m, maka r = 12 m
Menentukan luas tanah yang akan ditanami rumput
L = luas taman – luas kolam
L = (π r²) – (pxl)
l = (3,14.(12)²) – 9 x 6 = 452,16 – 54 = 398,16 m²
Maka biaya pemasangannya adalah
Biaya = Luas yang akan ditanami x (harga rumput + harga pasang)
Biaya = 398,16 x (Rp. 6.000 + Rp. 4.000) = 398,16 x Rp. 10.000 = Rp. 3.981.600,00
Jawaban C

Soal No.10

Jika selembar kertas dengan ukuran 50 cm x 60 cm akan dibuat lingkaran dengan diameter 44 cm. Maka sisa kertas tersebut adalah….

1. 197 cm²
2. 454,23 cm²
3. 867,34 cm²
4. 1480,24 cm²

PEMBAHASAN :
Diketahui:
panjang kertas = 60 cm
lebar kertas = 50 cm
d = 44 cm, maka r = 22 cm
Menentukan sisa kertas yang tidak terpakai
sisa = luas kertas – luas lingkaran
sisa = (p x l) – (πr²)
sisa = (60 x 50) – (3,14. (22)²) = 3000 – 1519,76
sisa = 1480,24 cm²
Jawaban D

Soal No.11

Daerah yang dibatasi atau diapit oleh dua garis jari-jari dan satu busur lingkaran disebut …

1. Tembereng
2. Juring
3. Segitiga
4. Tali busur

PEMBAHASAN :
Pada unsur-unsur lingkaran yang dimaksud dengan juring adalah daerah yang dibatasi atau diapit oleh dua garis jari-jari dan satu busur lingkaran. Sedangkan tembereng adalah daerah yang dibatasi oleh busur lingkaran dan tali busur lingkaran.
Jawaban B

Soal No.12

Sebuah lingkaran memiliki jari-jari 12 cm. panjang keliling lingkaran adalah … cm

1. 80,32
2. 78,55
3. 75,36
4. 72,31

PEMBAHASAN :
Diketahui:
r = 12 cm
π = 3,14

Menghitung panjang keliling lingkaran adalah sebagai berikut:
K = 2πr = 2 x 3,14 x 12 cm = 75,36 cm
Jawaban C

Soal No.13

Sebuah kolam berbentuk setengah lingkaran memiliki diameter 16 m. kolam tersebut pinggirannya akan dipasangi dengan warna keramik yang berbeda. Panjang batas kolam yang akan dipasangi keramik adalah … m.

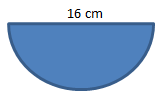
1. 41,12
2. 39,5
3. 35,09
4. 30,87

PEMBAHASAN :
Diketahui:
d = 16 m

Menentukan panjang batas kolam yang dipasangi keramik adalah sebagai berikut:

panjang batas kolam = ½ keliling lingkaran + diameter
.                                      = (½ x π x d) + d = (½ x 3,14 x 16 m) + 16 m = 41,12 m
Jawaban A

Soal No.14

Perhatikan gambar lingkaran di bawah ini!

Luas lingkaran di atas adalah 132,665 cm². Panjang jari-jari lingkaran tersebut adalah … cm.

1. 10
2. 11
3. 12
4. 13

PEMBAHASAN :
Diketahui:
L = 132,665 cm²
Maka, panjang jari-jari dapat dihitung sebagai berikut:
L = ¼ x L lingkaran
132,665 = ¼ x 3,14 x r²
132,665 = 0,785 x r²
r² = 169
r = 13
Jawaban D

Soal No.15

Perhatikan gambar di bawah ini!

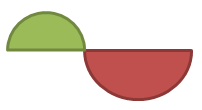
Apabila diameter lingkaran besar 30 cm dan diameter lingkaran kecil 20 cm. Luas daerah yang diarsir adalah …

1. 356,78
2. 452,42
3. 510,25
4. 555,13

PEMBAHASAN :
Diketahui:
Diameter lingkaran besar (d) = 30 cm atau r = ½ x 30 cm = 15 cm
Dameter lingkaran kecil (d) = 20 atau r = ½ x 20 cm = 10 cm

Maka, luas daerah yang diarsir dapat dihitung sebagai berikut:
Luas = Luas setengah lingkaran besar + luas setengah lingkaran kecil
.         = (½ x π x r²) + (½ x π x r²) = (½ x 3,14 x (15)²) + (½ x 3,14 x (10)²)
.         = 353,25 + 157 = 510,25
Jawaban C

Soal No.16

Seorang atlet berlatih di suatu arena olah raga dengan lapangan yang berbentuk seperti gambar di bawah ini.

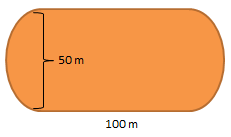
Panjang lintasan pada lapangan  ini adalah …

1. 452,42
2. 510,25
3. 555,13

PEMBAHASAN :
Diketahui:
Diameter lingkaran (d) = 50 m
panjang satu lintasan lurus = 100 m

Menghitung panjang lintasan sebagai berikut:
Panjang lintasan atau keliling = (2 x panjang lintasan lurus) + (keliling lingkaran)
.                                                      = (2 x 100 m) + (3,14 x 50 m) = 200 m + 157 m = 357 m
Jawaban A

Soal No.16

Seorang atlet berlatih di suatu arena olah raga dengan lapangan yang berbentuk seperti gambar di bawah ini.

Panjang lintasan pada lapangan  ini adalah …

1. 452,42
2. 510,25
3. 555,13

PEMBAHASAN :
Diketahui:
Diameter lingkaran (d) = 50 m
panjang satu lintasan lurus = 100 m

Menghitung panjang lintasan sebagai berikut:
Panjang lintasan atau keliling = (2 x panjang lintasan lurus) + (keliling lingkaran)
.                                                      = (2 x 100 m) + (3,14 x 50 m) = 200 m + 157 m = 357 m
Jawaban A

Soal No.17

Sebuah lingkaran dengan titik pusat di O dengan ∠POQ = 150⁰ dan panjang OP = 15 cm. Maka panjang busur PQ adalah …

1. 23,13 cm
2. 32,15 cm
3. 39,25 cm
4. 40,15 cm

PEMBAHASAN :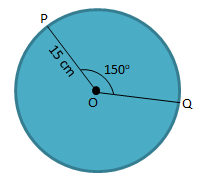

Diketahui:
OP = r = 15 cm
Titik pusat = titik O
∠POQ = 150

Dengan perbandingan, dapat dihitung panjang busur PQ sebagai berikut:

Jawaban C

Soal No.18

Sebuah lingkaran, diketahui panjang OA = 20 cm dan ∠AOB = 60⁰ . Luas juring AOB adalah … cm²

1. 200,5
2. 209,3
3. 214,5
4. 287,2

PEMBAHASAN :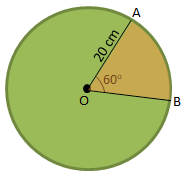

Diketahui:
OA = 20 cm
∠AOB = 60

Maka luas juring POQ dapat dihitung sebagai berikut: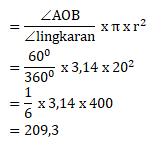

Jawaban C

Soal No.19

Sebuah lingkaran memiliki luas juring POQ = 45,6 cm² dan ∠POQ = 42. Jari-jari lingkaran tersebut adalah … cm.

1. 11,2
2. 12,3
3. 13,2
4. 14,5

PEMBAHASAN :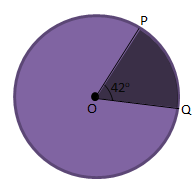

Diketahui:
luas juring POQ = 45,6 cm²
∠POQ = 42

Mencari luas lingkaran dapat dihitung sebagai berikut:

Untuk menghitung jari-jari lingkaran dapat dihitung sebagai berikut:

Menentukan jari-jari dari luas lingkaran
L = πr²
391 = 3,14 x r²
r² = = 125
r   = = 11,2 cm
Jawaban A

Soal No.20

Perhatikan gambar lingkaran di bawah ini!

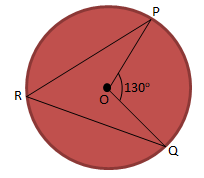
Diketahui ∠POQ = 130⁰ , maka ∠PRQ = … ⁰

1. 50
2. 65
3. 70
4. 75

PEMBAHASAN :
Diketahui:
∠POB = 130

Pada lingkaran luar segitiga seperti gambar diatas berlaku:
∠PRQ = ½ x ∠POQ = ½ x 130 = 65
Jawaban B

Soal No.21

Di dalam sebuah lingkaran terdapat sebuah segitiga siku-siku (lingkaran luar segitiga)  dengan  ∠A = 5x, ∠B = 90⁰  dan ∠C = 4x. Besar ∠ACB = …

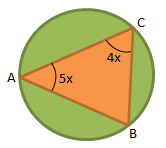
1. 20
2. 30
3. 40
4. 50

PEMBAHASAN :
Diketahui:
∠A = 5x
∠B = 90⁰
∠C = 4x
∠ABC = 180⁰

Menentukan nilai ∠C
∠A + ∠B + ∠C = 180⁰
5x   +  90⁰ + 4x = 180⁰
.                       9x = 90⁰
.                          x = 10
maka, ∠ACB = ∠C = 4x = 4 x 10 = 40
Jawaban C

Soal No.22

Pada lingkaran terdapat sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran atau disebut dengan sudut keliling lingkaran. Sudut keliling lingkaran memiliki sifat-sifat sebagai berikut, kecuali …

1. Sudut keliling harus bertolak belakang dengan sudut pusat
2. Sudut keliling suatu lingkaran yang menghadap diameter lingkaran, maka besar sudut keliling sama dengan 90⁰ .
3. Sudut-sudut keliling yang menghadap busur yang sama, maka besar sudut-sudut keliling tersebut akan sama.
4. Jumlah sudut keliling yang saling berhadapan adalah 180⁰ .

PEMBAHASAN :
Sifat-sifat sudut keliling adalah:

• Apabila sudut keliling suatu lingkaran menghadap diameter lingkaran, maka besar sudut keliling sama dengan 90⁰ .
• Apabila sudut-sudut keliling menghadap busur yang sama, maka besar sudut-sudut keliling tersebut adalah sama.
• Jumlah sudut keliling yang saling berhadapan adalah 180⁰ .

Jawaban A

Soal No.23

Daerah yang dibatasi oleh busur lingkaran dan tali busur lingkaran adalah …

1. Tali busur
2. Apotema
3. Tembereng
4. Busur

PEMBAHASAN :

• Tali busur: garis lurus yang menghubungkan garis lengkung busur lingkaran pada keliling lingkaran tetapi tidak melewati titik pusat lingkaran.
• Apotema: garis tegak lurus dengan tali busur merupakan jarak terpendek antara tali busur dengan titik pusat lingkaran.
• Tembereng: daerah yang dibatasi oleh busur lingkaran dan tali busur lingkaran.
• Busur: garis lengkung pada keliling lingkaran.

Jawaban C

Soal No.24

Sebuah lingkaran memiliki keliling 94,2 cm. Maka luas lingkaran adalah … cm.

1. 698,6
2. 706,5
3. 728,2
4. 755,6

PEMBAHASAN :
Diketahui:
K = 94,2 cm
π = 3,14

Menentukan panjang jari-jari lingkaran dapat dihitung sebagai berikut:
K = 2πr
94,2 = 2 x 3,14 x r
94,2 = 6,28 x r
r  = 15 cm

Maka, luas lingkaran dapat dihitung sebagai berikut:
L = πr² = 3,14 x 15² = 706,5 cm²
Jawaban B

Soal No.25

Diketahui dua buah lingkaran P dan Q, masing-masing memiliki jari jari lingkaran P adalah 2 kali jari-jari lingkaran Q. Besar perbandingan luas lingkaran P dan Q adalah …

1. 4 : 1
2. 3 : 1
3. 2 : 1
4. 1 : 1

PEMBAHASAN :
Diketahui:
r_p = 2 x r_Q

Maka untuk menghitung besar perbandingan luas lingkaran P dan Q adalah: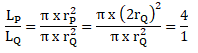

Maka perbandingannya adalah 4 : 1
Jawaban A

Soal No.26

Perhatikan gambar di bawah ini!

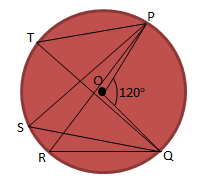
Maka ∠PTQ = …

1. 50
2. 60
3. 70
4. 80

PEMBAHASAN :
Diketahui:
∠POQ = 120

Pada lingkaran luar segitiga seperti gambar diatas berlaku:
∠PTQ = ½ x ∠POQ = ½ x 120 = 60
Jawaban B

Soal No.27

Banyak garis singgung yang dapat melalui titik yang berada di luar lingkaran adalah … buah.

1. 1
2. 2
3. 3
4. 4

PEMBAHASAN :
Garis singgung lingkaran  adalah garis yang memotong lingkaran tepat di satu titik pada keliling lingkaran.
Jawaban A

Soal No.28

Dua buah lingkaran yang berpusat di titik P dan Q, jari-jari lingkaran P adalah 7 cm dan jari-jari lingkaran Q adalah 5 cm. Jarak kedua pusat lingkaran tersebut 15 cm. sehingga panjang garis singgung persekutuan dalam kedua lingkaran tersebut adalah …

1. 9 cm
2. 10 cm
3. 11 cm
4. 12 cm

PEMBAHASAN :
Diketahui:
R = 7 cm
r = 5 cm
k = 15 cm

maka panjang garis singgung persekutuan dalam (d) dapat dihitung sebagai berikut: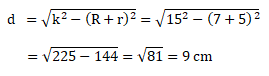

Jawaban A

Soal No.29

Sebuah segitiga memiliki panjang sisi 15 cm, 20 cm, dan 25 cm. Maka panjang jari-jari lingkaran luar segitiga tersebut adalah … cm.

1. 10,5
2. 11
3. 12,5
4. 13

PEMBAHASAN :
Diketahui:
Panjang sisi a = 15 cm
Panjang sisi b = 20 cm
Panjang sisi c = 25 cm

Menentukan luas segitiga sebagai berikut:
L = ½ x 15 cm x 20 cm
.  = 150 cm²

Menentukan jari-jari lingkaran luar segitiga adalah: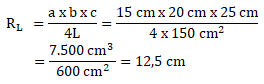

Jawaban C

Soal No.30

Dari soal no. 29 panjang jari-jari lingkaran dalamnya … cm.

1. 2,9
2. 4,5
3. 5
4. 5,4

PEMBAHASAN :
Diketahui:
Panjang sisi a = 15 cm
Panjang sisi b = 20 cm
Panjang sisi c = 25 cm

Menentukan luas segitiga sebagai berikut:
L = ½ x 15 cm x 20 cm
.  = 150 cm²

Menentukan panjang jari-jari lingkaran dalamnya sebagai berikut:
s = ½ x keliling segitiga
.  =  ½  x (15 cm +20 cm + 25 cm)
.  = 30 cm

Maka jari-jari lingkaran dalamnya adalah

Jawaban C

Soal No.31

Perhatikan gambar di bawah ini!

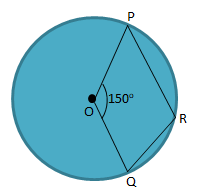
Besar sudut ∠PRQ adalah … ⁰

1. 95
2. 90
3. 205
4. 105

PEMBAHASAN :
Diketahui:
∠juring kecil POQ = 150
∠juring besar POQ = 360⁰ – 150⁰ = 210

Maka besar ∠PRQ = ½ x 210⁰ = 105
Jawaban D

Soal No.32

Dua buah lingkaran dengan jari-jarinya masing-masing 12 cm dan 6 cm dengan jarak kedua titik pusat lingkaran 36 cm. Panjang garis singgung persekutuan dalamnya adalah …

1. 31,1
2. 26,8
3. 33,9
4. 41,2

PEMBAHASAN :
Diketahui:
R = 12 cm
r = 6 cm
k = 36 cm

Untuk menghitung panjang garis singgung persekutuan dalam (d) adalah:

Jawaban A

Soal No.33

Dua buah lingkaran dengan jari-jarinya masing-masing 12 cm dan 6 cm dengan jarak kedua titik pusat lingkaran 36 cm. Panjang garis singgung persekutuan dalamnya adalah …

1. 31,1
2. 26,8
3. 33,9
4. 41,2

PEMBAHASAN :
Diketahui:
R = 12 cm
r = 6 cm
k = 36 cm

Untuk menghitung panjang garis singgung persekutuan dalam (d) adalah:

Jawaban A

Soal No.34

Terdapat dua buah lingkaran P dan Q dengan jari jari P = 10 cm dan jari-jari Q = 6 cm. Panjang garis persekutuan dalam = 42 cm. Maka jarak antara titik pusat P dan Q  = … cm.

1. 43
2. 45
3. 37
4. 39

PEMBAHASAN :
Diketahui:
R = 10 cm
r  = 6 cm
d = 42 cm

Rumus yang berlaku untuk garis singgung persekutuan dalam untuk menentukan jarak antara titik pusat Pdan Q sebagai berikut: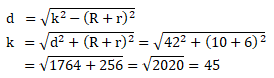

Jawaban B

Soal No.35

Perhatikan gambar di bawah ini!

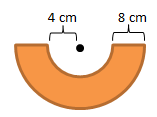
Luas daerah yang diarsir pada gambar tersebut adalah …

1. 43
2. 45
3. 37
4. 39

PEMBAHASAN :
Diketahui:
Jari-jari lingkaran besar = r_b = 8 cm + 4 cm = 12 cm
Jari-jari lingkaran kecil = r_k = 8 cm

Maka untuk menghitung luas daerah yang diarsir sebagai berikut:
Luas daerah yang diarsir = ½ luas lingkaran besar – ½ luas lingkaran kecil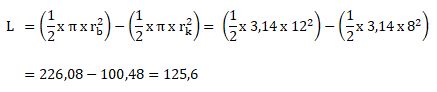

Jawaban D

Soal No.36

Perhatikan gambar di bawah ini!

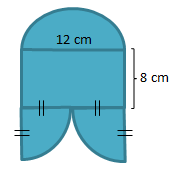
Besar keliling dari gambar yang diarsir adalah … cm.

1. 75,76
2. 77,68
3. 81,12
4. 85,32

PEMBAHASAN :
Menentukan keliling setengah lingkaran
K = ½  x (π x d)
K  = ½  x (3,14 x 12 cm) = 18,84 cm

Menentukan keliling persegi panjang
K = 2 x (p + l)
K= 2 x (12 cm + 8 cm) = 40 cm

Menentukan keliling seperempat dua lingkaran
K = 2 x (1/4 x π x d)
K = 2 x (1/4 x 3,14 x 12 cm) = 18,84 cm

Maka besar keliling gambar yang diarsir adalah 18,84 cm + 40 cm + 18,84 cm = 77,68 cm
Jawaban B

Soal No.37

Luas daerah yang diarsir pada soal no.36 adalah … cm..

1. 178,12
2. 180,43
3. 197,36
4. 209,04

PEMBAHASAN :
Menentukan luas setengah lingkaran
L = ½  x (π x r²)
L = ½  x (3,14 x 6² cm) = 56,52 cm

Menentukan luas persegi panjang
L = p x l = 12 cm x 8 cm = 96 cm²

Menentukan luas seperempat lingkaran
L = 2 x (1/4 x π x r²)
L = 2 x (1/4 x 3,14 x 6² cm) = 56,52 cm

Maka besar keliling gambar yang diarsir adalah 56,52 cm + 96 cm + 18,84 cm = 209,04 cm
Jawaban D

Soal No.38

Sebuah lingkaran dengan titik pusat di O. titik P dan Q terletak pada keliling lingkaran dengan panjang OP = OQ = 30 cm dan ∠POQ = 60⁰ . Maka panjang busur PQ adalah … cm.

1. 28,2
2. 31,4
3. 37,5
4. 40,3

PEMBAHASAN :
Diketahui:
OP = OQ = 30 cm
∠POQ = 60⁰

Maka, untuk menghitung panjang busur PQ adalah sebagai berikut:

Jawaban D

Soal No.39

Perhatikan gambar di bawah ini!

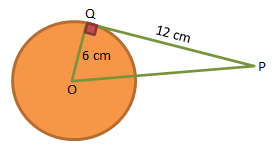
Panjang jarak dari titik O ke P = … cm

1. 13,4
2. 14
3. 14,9
4. 15

PEMBAHASAN :
Diketahui:
OQ = 6 cm
PQ = 12 cm
∠PQO = sudut siku-siku

Maka untuk menghitung panjang OP berlaku sebagai berikut: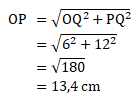

Jawaban A

Soal No.40

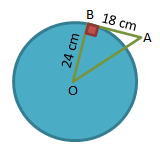
Keliling lingkaran pada gambar di atas adalah … cm.

1. 400
2. 300
3. 200
4. 100

PEMBAHASAN :
Diketahui:
∠ABO = sudut siku-siku
AB = 18 cm
OA = 24 cm

Menentukan jari-jari lingkaran sebagai berikut: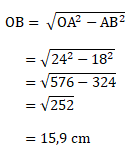

Maka keliling lingkaran dapat dihitung sebagai berikut:
K = 2πr
K = 2 x 3,14 x 15,9 cm = 100 cm
Jawaban D