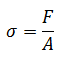Untuk Pembelajaran selanjutnya…
Merupakan kemampuan suatu benda untuk kembali ke keadaan semula setelah gaya yang dikenakan padanya dilepaskan. Sifat elastis suatu bahan berkaitan erat dengan modulus elastis. Modulus elastis disebut juga modulus Young. Modulus elastis adalah perbandingan antara tegangan dan regangan yang dialami oleh suatu benda.
Tegangan
merupakan hasil bagi antara gaya tarik yang dialami benda dengan luas penampangnya, dan dirumuskan:

Keterangan:
s : tegangan (N/m2)
F : gaya (N)
A : luas penampang (m2)
Regangan
merupakan hasil bagi antara pertambahan panjang dengan panjang awal, dan dirumuskan:
Keterangan:
e : regangan (tanpa satuan)
∆l : pertambahan panjang (m)
lo : panjang awal (m)
l : panjang akhir (m)
Modulus Elastis
Yaitu perbandingan antara tegangan dan regangan yang dialami oleh suatu benda, dan dirumuskan:
Hukum Hooke
Jika gaya tarik tidak melampaui batas elastisitas pegas, pertambahan panjang pegas berbanding lurus dengan gaya tariknya. Jika dirumuskan sebagai berikut:
F = k.Δx
Keterangan:
F = gaya pada pegas (N)
k = konstanta gaya
Δx = pertambahan panjang (m)
Hukum Hooke Untuk Susunan Pegas
Pegas Tersusun Seri

Sumber gambar : https://sumberbelajar.belajar.kemdikbud.go.id/
- Tetapan pegas pengganti seri

- Gaya tarik yang dialami tiap pegas akan sama besar
F1 = F2 = F3 - Pertambahan panjang pegas pengganti seri = total pertambahan panjang tiap-tiap pegas
Δx = Δx1 + Δx2
Pegas Tersusun Paralel
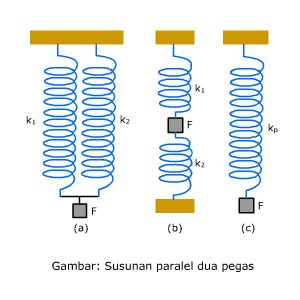
Sumber gambar : https://sumberbelajar.belajar.kemdikbud.go.id/
- Tetapan pegas pengganti paralel
kp = k1 + k2 - Gaya tarik pada pegas pengganti F = total gaya tarik pada tiap pegas
F = F1 + F2 - Gaya tarik yang dialami tiap pegas akan sama besar
Δx = Δx1 = Δx2
Soal No.1 (UTBK 2019)
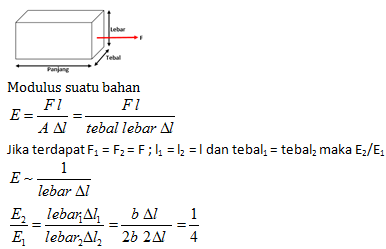
Seutas pita elastis memiliki panjang l dan lebar b. Jika salah satu ujung pita itu diklem pada dinding dan ujung yang lain ditarik dengan gaya sebesar F, pita itu bertambah panjang sebesar Δl. Pita kedua memiliki panjang l dan lebar 2b serta ketebalan yang sama. Jika salah satu ujung pita kedua itu diklem pada dinding dan ujung yang lain ditarikdengan gaya sebesar F, pita bertambah panjang 2Δl. Rasio modulus Young pita kedua dan modulus Young pita pertama adalah….
- 1 : 4
- 1 : 2
- 1 : 1
- 2 : 1
- 4 : 1
Soal No.2 (SBMPTN 2018)
Sebuah sistem mekanik diperlihatkan pada gambar. Sudut kemiringan bidang θ = 30 dan bidang miring licin. Sistem berada dalam keadaan setimbang serta massa katrol dan massa pegas diabaikan. Jika setiap massa dijadikan dua kali semula, salah satu cara yang dapat dilakukan agar sistem tetap setimbang adalah….
- konstanta pegas tetap dan pertambahan panjang pegas menjadi 2 kali semula
- konstanta pegas menjadi 0,5 kali semula dan pertambahan panjang pegas menjadi 2 kali semula
- konstanta pegas tetap dan pertambahan panjang pegas menjadi setengah kali semula
- konstanta pegas menjadi dua kali semula dan pertambahan panjang pegas tetap
- konstanta pegas tetap dan pertambahan panjang pegas menjadi 4 kali semula
PEMBAHASAN :
Menggambarkan gaya – gaya yang terlibat pada benda.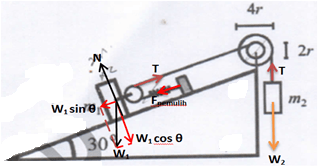
Untuk mengetahui situasi pegas (pada komponen sumbu x) maka yang ditinjau hanya pada arah sumbu ini.
Dalam kondisi setimbang
ΣFx = 0
(kita anggap benda 1 bergerak tepat akan atas atau benda 2 tepat akan bergerak ke bawah, maka pada arah ini gaya bernilai positif)
w2– T + T – w1 sin θ – Fpemulih = 0
w2 – w1 sin θ = Fpemulih
w2 – w1 sin 30 = Fpemulih
m2g – m1g ½ = ½ k Δx2 (Situasi 1)
Jika semua massa dijadikan dua kali semula
m2’ = 2m2 dan m1’ = 2m1
maka:
m2‘g – m1’g ½ = ½ k’ Δx2 (Situasi 2)
2m2g – 2m1g ½ = ½ k’ Δx2
2( m2g – m1g ½) = ½ k’ Δx2
agar sistem tetap setimbang (tidak bergerak) Δx harus dikondisikan tetap konsekuensinya
k’ = 2k
Artinya konstanta pegas menjadi 2 kali semula dan pertambahan panjang pegas tetap
Jawaban D
Soal No.3 (SBMPTN 2018)
Tiang baja berbentuk silinder pejal digunakan untuk menyangga sebuah beban. Akibat pembebanan tersebut, tiang baja mengalami pemendekan sebesar Δl. Jika digunakan dua tiang baja identik yang disambung dan digunakan untuk menyangga beban yang sama, pemendekan yang dialami oleh setiap tiang tersebut adalah…
- 4(Δl)
- 2(Δl)
- Δl
- (Δl)/2
- (Δl)/4
PEMBAHASAN :
Situasi 1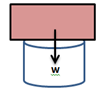
Jika situasi ini dianggap pegas maka
F = k ΔL1
mg = k ΔL1 (1)
Situasi 2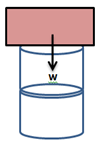
Jika situasi ini dianggap pegas yang dirangkai seri maka
F = kseri ΔL2
mg = = kseri ΔL2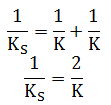
KS = ½ K
mg = ½ K ΔL2 (2)
Subsitusi 1 ke 2
K ΔL1 = ½ K ΔL2
ΔL1 = ½ ΔL2
ΔL2 = 2 ΔL1
ΔL2 merupakan pemendekan 2 buah silinder pejal yang identik
ΔL2 = 2ΔLsilinder
2ΔL1 = 2ΔLsilinder
ΔLsilinder = ΔL1
Jawaban B
Soal No.4
Sebuah pegas memiliki tetapan 5 Nm-1. Berapakah massa beban yang harus digantungkan agar pegas bertambah panjang 98 mm? Berapakah periodenya jika beban tersebut digetarkan? (g = 9,8 m s-2)
Soal No.5
Diketahui seutas kawat dengan diameter 4 mm dan memiliki panjang 5 m dan digantung secara vertikal dan diberi beban seberat 50 kg. Jika kawat tersebut tertarik sejauh 3 mm tentukan :
a. tegangan kawat
b. regangan kawat
c. modulus elastik bahan kawat
(g = 10 m/s2; π = 22/7)
PEMBAHASAN :
Diketahui:
Diameter (d) = 3,5 mm
Jari-jari (r) = 4 mm/2 = 2 x 10-3 m
L = 5 m
m = 50 kg
ΔL = 3 mm = 3 x 10-3 m
- Menentukan tegangan kawat
Menggunakan rumus berikut: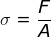
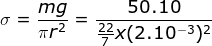
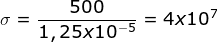
- Menentukan regangan dapat ditentukan dengan rumusan
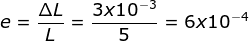
- Menentukan Nodukus elastis
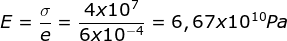
Soal No.6
Jika diketahui modulus Young alumunium = 7,0 x 1010 Pa. Tentukan gaya yang diperlukan agar kawat alumunium tertarik sepanjang 1 mm dengan panjang kawat 800 mm dan garis tengahnya 2,0 mm?
PEMBAHASAN :
Diketahui:
E = 7,0 x 1010
Lo = 800 mm
ΔL = 1 mm
d = 2,0 mm
r = 1/2 x 2 mm = 1 mm = 10-3 m
A = πr2 = 3,14. (10-3)2 = 3,14. 10-6
Menentukan gaya tarik dari modulus elastis![]() , maka:
, maka:![]()
Soal No.7
Tentukan diameter minimum agar kawat alumunium tidak kehilangan sifat elastisnya oleh gaya 800π. Diketahui batas tegangan tarik alumunium adalah 200 MPa.
PEMBAHASAN :
Diketahui:
Gaya tarik = 800π N
Tegangan tarik maksimum = 200 MPa = 2 x 108 Pa
Menentukan diameter minimum dari rumusan tegangan![]()
![]()
![]()
![]()
![]()
Soal No.8
Senar diketahui ditarik dengan gaya 140 N yang memiliki panjang 80 cm dan diameter 1/π cm. Diketahui modulus elastiknya 2,0 x 1011 N/m2. Tentukan:
a. tegangannya
b. pertambahan panjangnya
c. panjang akhir setelah ditarik
d. regangannya (π = 22/7)
PEMBAHASAN :
Diketahui :
F = 140 N
Lo = 80 cm = 0,8 m
d = 1/π cm = 1/π x 10-2 m
E = 2,0 x 1011 N/m2
- Menentukan tegangan

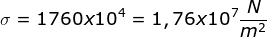
- Menentukan pertambahan panjang dari rumusan modulus Young
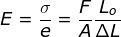
Maka pertambahan panjangnya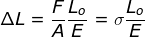
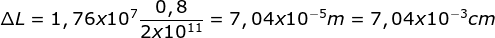
- Menentukan panjang senar jika ditarik
ΔL = L – Lo
L = ΔL + Lo = 80 cm + 0,0074 cm = 80,00704 cm - Menentukan regangan
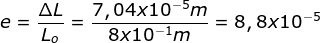
Soal No.9
Sebuah silinder memiliki panjang 1 meter diketahui modulus elastisnya = 1,6 x 1010 N/m2 memiliki luas penampang 1,25 x 10-3 m2 ditarik dengan gaya 2.500 N. Tentukan:
a. tegangan
b. regangan
c. pertambahan volume
PEMBAHASAN :
Diketahui:
Lo = 1 m
A = 1,25 x 10-3 m2
F = 2500 N
E = 1,6 x 1010 N/m2
- Menentukan tegangan
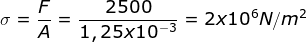
- Menentukan regangan
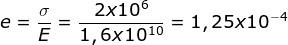
- Menentukan pertambahan volume
Pertambahan volume ditentukan dengan rumus
ΔV = A.ΔL
Dapat ditentukan dari rumus
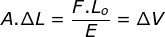
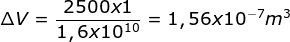
Soal No.10
Kabel penahan lift memiliki luas penampang 6 cm2 digunkanan untuk menahan lift yang bertanya 24.000 N. Jika tegangan kabel tidak boleh melebihi 10 persen dari batas elastisitas kabel yaitu 32.000 N/cm2, berapa percepatan ke atas maksimum yang diperbolehkan
PEMBAHASAN :
Diketahui:
A = 6 cm2
Wlift = 24.000 N
Tegangan maksimal (σmaks) = 20% dari batas elastisitas kabel= 20% x 32.000 N/cm2 = 6.400 N/cm2
Menentukan gaya maksimum (Fmaks)![]()
![]()
Gaya yang bekerja adalah gaya ke atas Fm dan berat liwt W lift, sehingga menurut hukum II Newton,
∑F = m.a
+Fm – mg = m am![]()
Jika W = mg = 24000![]()
Maka percepatan ke atas maksimum (am) adalah![]()
Soal No.11
Pegas yang panjangnya 15 cm digantung secara vertikal. Jika diregangkan dengan gaya sebesar 0,5 N sehingga panjangnya menjadi 27 cm. Tentukan panjang pegas jika direnggangkan oleh gaya 0,7 N?
PEMBAHASAN :
Diketahui:
Lo = 15 cm
pertambahan panjang dengan gaya 0,5 N
x = L – Lo = 27 – 15 = 12 cm = 12 x 10-2 m
Untuk menentukan panjang pegas L ketika ditarik oleh gaya 0,7 N maka kita bisa membandingkannya![]()
nilai k sama, maka bisa dicoret sehingga menjadi:![]()
![]()
![]()
Maka panjang pegas L menjadi
L = Lo + x = 15 cm + 16,8 cm = 31,8 cm
Soal No.12
Seutas kawat ditarik oleh gaya 300 N sehingga bertambah panjang 0,25 mm. Berapakah energi potensialnya.
PEMBAHASAN :
Diketahui:
F = 300 N
Pertambahan panjang (x) = 0,25 mm = 2,5 x 10-4 m
Menentukan energi potensial
EP = 1/2 F.x = 1/2. 300. 2,5 x 10-4 = 3,75 x 10-2
Soal No.13
Pegas memiliki panjang 10 cm digantung secara vertikal. Kemudian bagian bawahnya di beri beban 100 gram sehingga berubah panjangnya menjadi 15 cm. Jika beban tersebut ditarik 5 cm ke bawah. Tentukan energi potensial elastik pegas (g = 10 m/s2)
PEMBAHASAN :
diketahui :
m = 100 gram = 10-1 kg
x = 15 – 10 = 5 cm = 5. 10-2 m
Besarnya gaya tarik sebesar berat beban
F = m.g = 10-1. 10 = 1 newton
Maka besarnya energi potensialnya adalah
EP = 1/2 F. x = 1/2 1.5.10-2 = 2,5. 10-2 joule
Soal No.14
Jok suatu motor turun 5 cm ketika pengendara bermassa 50 kg duduk di atasnya. Jika shockbreaker dianggap pegas. Tentukan energi potensialnya jika seseorang bermassa 75 kg naik sepeda motor tersebut? (g = 10 m/s2)
PEMBAHASAN :
Diketahui:
m = 50 kg, maka berat:
F1 = m.g = 50. 10 = 500 N
F2 = m.g = 75. 10 = 750 N
x1 = 5 cm = 5 x 10-2
Menentukan tetapan gas (k)
F1 = k.x1![]()
Menentukan penyusutan pegas saat diberikan beban 75 kg
F2 = k.x2![]()
Menentukan energi potensial saat diberi beban 75 kg
EP = 1/2.kx2 = 1/2. 104. (7,5 x 10-2)2 = 28,125 joule
Soal No.15
Seorang penerjun diikat dengan tali yang elastis. Terjun dari ketinggian 60 m. Panjang tali 20 meter dengan tetapan elastik 225 N/m. Jika massa penerjun tersebut adalah 70 kg dan g = 10 m/s2, tentukanlah apakah atlet tersebut sampai ke tanah atau tidak.
PEMBAHASAN :
Diketahui:
m = 70 kg
g = 10 m/s2
h = 60 m
Lo = 20 m
k = 250 N/m
Menentukan atlet tersebut sampai ke tanah atau tidak bisa ditentukan menggunakan hukum kekekalan energi mekanik. Dimana energi potensial maksimum di titik terendah tali = energi potensial elastik tali.
Epmaks = EPtali
m.g.h = 1/2 kx2![]()
![]()
Maka titik terendahnya adalah
L = Lo + x = 20 + 18,33 m = 38,33 m
L < h
38,33 m< 60 m
Artinya atlet belum sampai ke tanah
Soal No.16
Jika sebuah pegas yang digantung pada langit-langit lift kemudian dibagian bawahnya di beri beban 40 gram. Pada kondisi diam pegas bertambah panjang 10 cm. Tentukan pertambahan pegas ketika:
a. lift bergerak ke atas dengan percepatan 5 m/s2
b. lift bergerak ke bawah dengan percepatan 5 m/s2
(percepatan gravitasi = 10 m/s2)
PEMBAHASAN :
Tinjau benda:

Diketahui:
m = 40 gram = 4 x 10-2 kg
g = 10 m/s2
x = 10 cm = 0,1 m
menentukan konstanta pegas (k) ditinjau dari hukum II Newton:
∑F = ma
+kx -mg = 0
kx = mg![]()
- Menentukan pertambahan panjang pegas ketika lift bergerak ke atas dengan a = 4 m/s2
ΣF = ma
+kx – mg = ma
kx = m (a + g)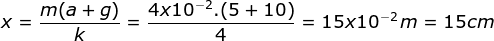
- Menentukan pertambahan panjangpegas ketika lift sedang bergerak ke bawahh dengan a = -4
ΣF = ma
+kx – mg = ma
kx = m (a + g)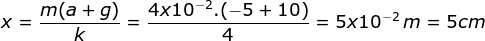
Soal No.17
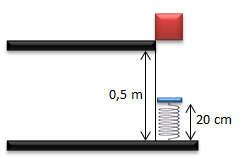
Sebuah balok jatuh dari meja yang memiliki ketinggian 0,5 m. Balok tepat jatuh di ujung sebuah pegas yang memiliki tetapan 2,8 kN/m. Jika tinggi pegas semula adalah 20 cm. Ketika jatuh bendah tersebut menekan pegas sehingga memiliki tinggi terendah 10 cm. Tentukan massa balok. (g = 10 m/s2)
PEMBAHASAN :
Diketahui:
h1 = 50 cm = 0,5 m
h2 = 10 cm = 0,1 m
h1 – h2 = 0,5 – 0,1 m = 0,4 m
k = 2,8 kN/m = 2,8 x 103 N/m
g = 10 m/s2
x = 20- 10 = 10 cm = 0,1 m
Kondisi benda awal dan akhir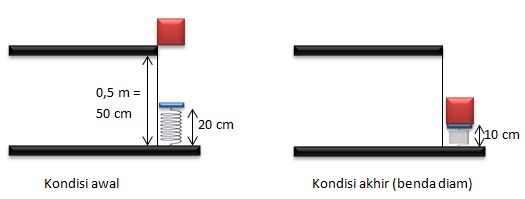
berlaku hukum kekekalan energi mekanik
(EPbalok + EPpegas)awal = (EPbalok + EPpegas)akhir
mgh1 + 0 = mgh2 + 1/2 kx2![]()
![]()
Soal No.18
Tentukan nilai perbandingan period susunan pegas pada a dan b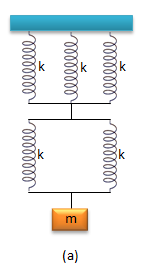

PEMBAHASAN :
Menentukan tetapan pegas pengganti
- ka = (k paralel k paralel k)seri (k paralel k)
ka = (k + k + k) seri (k + k)
ka = 3k seri 2k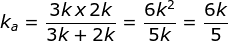
- kb = (k paralel 2k) seri (k paralel 2k)
kb = (k + 2k) seri (k + 2k)
kb = 3k seri 3k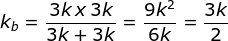
menentukan perbandingan period pegas a dan b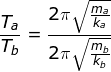
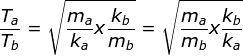
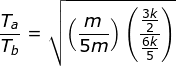
![]()
Jadi Ta : Tb = 1 : 2
Soal No.19
Sebuah pegas memerlukan usaha 70 joule untuk meregang sepanjang 5 cm. Tentukan usaha yang diperlukan untuk meregangkan pegas tersebut sepanjang 35 cm
PEMBAHASAN :
Diketahui:
W1 = 70 joule
x1 = 5 cm
x2 = 3 cm
Menentukan usaha yang diperlukan untuk meregangkan pegas 3 cm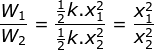
![]()
![]()
Semoga Bermanfaat