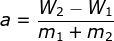Untuk Pembelajaran selanjutnya…
Hukum Newton
Hukum I Newton
“jika resultan gaya pada suatu benda sama dengan nol, maka benda mula-mula diam akan senantiasa diam, sedangkan benda yang mula-mula bergerak akan terus bergerak dengan kecepatan tetap”. Dinyatakan sebagai berikut.
ΣF = 0
Digunakan untuk benda diam atau benda bergerak lurus.
Hukum II Newton
“Percepatan yang dihasilkan oleh resultan gaya yang bekerja pada suatu benda berbanding lurus dengan resultan gaya, searah dengan resultan gaya, dan berbanding terbalik dengan massa benda”. Dinyatakan sebagai berikut .
∑F=ma
Keterangan :
∑F : resultan gaya (Newton)
m : massa benda (kg)
a : percepatan
Hukum III Newton
Energi memiliki arti sebagai kemampuan untuk melakukan usaha. Contoh : energi potensial, dan energi kinetik. Dinyatakan dengan:
Faksi = -Freaksi
PENERAPAN HUKUM NEWTON
Benda digantungkan dengan tali dan di gerakkan
persamaannya sebagai berikut.
∑F = ma
T-mg = ma
T = mg + ma
Keterangan :
T : tegangan tali (N)
m : massa benda (kg)
g : percepatan gravitasi (m/s2)
a : percepatan (m/s2)
Digerakkan kebawah dengan percepatan a, persamaannya sebagai berikut.
∑F = ma
Mg – T = ma
T = mg – ma
Orang yang berada di lift
Lift diam atau bergerak dengan v konstan.
∑F = 0
N – W = 0
N = W
lift dipercepat kebawah
∑F = ma
W – N = ma
N = W – ma
N = mg – ma
Benda yang digantung dengan seutas tali melalui katrol
dengan dua utas tali dalam keadaan setimbang. Jika masa tali dan massa katrol diabaikan dan W₂ > W₁ maka percepatan benda nya sebagai berikut.
![]()
Benda yang di gantungkan dengan dua utas tali dalam keadaan setimbang
![]()
Gaya normal dan Gaya Gesekan
Gaya normal adalah gaya yang ditimbulkan oleh alas bidang suatu benda, arahnya tegak lurus terhadap bidang tersebut. Sedangkan gaya gesek adalah gaya yang ditimbulkan akibat persentuhan langsung antara dua permukaan, arahnya selalu berlawanan dengan arah gerak benda. Dibagi menjadi dua macam, yaitu :
- Gaya gesek statis ( fs) yaitu gaya gesekan yang bekerja pada benda ketika benda dalam keadaan diam.
- Gaya gesek kinetik ( fk) adalah gaya gesekan yang bekerja pada benda ketika benda mengalami pergerakan.
Gerak atau diamnya suatu benda diperoleh berdasarkan beberapa aturan, yaitu :
- Jika F ˂ fs’ maka benda dalam keadaan diam.
-
Jika F = fs’ maka benda akan tepat akan bergerak.
-
Jika F > fs’ maka benda bergerak dan gaya gesekan statis fs berubah menjadi fk
Hubungan antara gaya gesek, gaya normal, dan koefisien gaya gesek dituliskan sebagai berikut.
-
Gaya gesek statis : fs = µs N.
-
Gaya gesek kinetis : fk = µk N.
Jika sebuah balok yang beratnya w diletakkan pada bidang datar dan balok tidak dipengaruhi gaya luar maka besar gaya normal tersebut adalah :
N = w
Jika sebuah balok yang massanya m berada pada bidang miring licin yang memiliki sudut kemiringan maka besarnya gaya normal dapat ditentukan dengan :
N = w cos θ
Hukum Gravitasi Newton
“Gaya gravitasi antara dua benda berbanding lurus dengan massa setiap benda dan berbanding terbalik dengan kuadrat jarak antara keduanya”. Ditulis dalam persamaan reaksi berikut:
![]()
Keterangan :
F12 = F21 : gaya tarik menarik antara kedua benda (N)
G : tetapan umum gravitasi = 6,672 x 10 23 Nm2/kg2
m1 : massa benda 1 (kg)
m2 : massa benda 2 (kg)
r2 : jarak antara kedua benda (m)
Kuat medan gravitasi
kuat medan gravitasi diartikan sebagai gaya yang bekerja pada satuan massa yang terjadi dalam medan gravitasi. Kuat medan gravitasi ditulis dalam persamaan matematis berikut.![]()
Keterangan :
M : massa benda yang menghasilkan percepatan gravitasi (kg)
r : jarak titik ke pusat massa (kg)
Perbandingan percepatan gravitasi dua buah planet
Dinyatakan dalam persamaan berikut.
![]()
Hukum Kepler tentang planet
- Hukum I Kepler “semua planet bergerak pada lintasan elips mengitari matahari dengan matahari berada di salah satu fokus elips”.
- Hukum II Kepler “suatu garis khayal yang menghubungkan matahari dengan planet menyapu luas juring yang sama dalam selang waktu yang sama”.
- Hukum III Kepler “perbandingan kuadrat periode terhadap pangkat tiga dari setengah sumbu panjang elips adalah sama untuk semua planet”. Hukum III Kepler jika dituliskan dalam persamaan matematis sebagai berikut.

Keterangan :
T : periode revolusi
R : jari- jari rata-rata orbit planet
Gaya Pegas
Tegangan, Regangan, dan Modulus Elastik
Tegangan
Tegangan merupakan perbandingan antara gaya yang diberikan dengan luas penumpang benda. Dapat ditulis sebagai berikut:![]()
Keterangan :
F : Gaya
A : Luas penumpang
Regangan
Regangan merupakan perbandingan antara perubahan panjang dan panjang mula-mula. Dapat ditulis sebagai berikut:![]()
Keterangan :
perubahan panjang (m)
I : panjang mula-mula (m)
Modulus elastik
Hukum Hooke dan Energi Potensial Pegas
Secara matematis hukum Hooke dapat di tuliskan sebagai berikut.
F = kx
Keterangan :
F : gaya (Newton)
K : konstanta pegas (N/m)
X : pertambahan panjang (m)
Pegas dapat disusun secara seri, pararel, maupun campuran antara seri dan pararel. Pegas yang tersusun baik secara seri, pararel, maupun campuran akan diketahui konstanta pegas total.
- Pegas tersusun secara seri
![]()
- Pegas tersusun secara pararel
ktot = k1+ k2+…kn
Energi potensial pegas dirumuskan sebagai berikut.
Ep = kx2 atau Ep = kx
Informasi berikut digunakan untuk menjawab soal no 1 dan 2
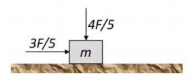
Suatu balok bermassa 2 kg yang berada pada suatu bidang datar licin mengalami dua gaya konstan seperti ditunjukkan gambar dengan F = 10 newton. Kecepatan pada saat t = 0 sekon adalah 2 m/s ke arah kiri.
Soal No.1 (UTBK 2019)
Besar gaya normal yang bekerja pada balok (dalam satuan newton) dan percepatan balok (dalam satuan m/s2) berturut-turut sama dengan…
- 12 dan 3
- 18 dan 6
- 28 dan 3
- 34 dan 6
- 40 dan 3
PEMBAHASAN :
Menggambarkan gaya – gaya yang terlibat pada benda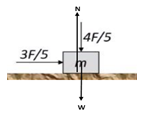
F = 10 newton
Massa = 2 kg
Pada saat t = 0 benda memiliki vo = 2 m/s ke kiri
Menentukan gaya normal (N)
Searah sumbu Y kondisi benda diam
ΣFY = 0
ΣFatas = ΣFbawah
N = 4F/5 + w
N = 4 (10)/5 + mg
N = 8 + 2 (10)
N = 28 newton
Menentukan percepatan (a)
Searah sumbu x kondisi benda bergerak
ΣF = m a
3F/5 = 2a
3(10)/5 = 2a
6 = 2a
a = 3 m/s2
Jawaban C
Soal No.2 (UTBK 2019)
Perpindahan balok selama t detik pertama adalah….
- (2t – 3t2) m
- (-2t + 3t2) m
- (2t – 4,5t2) m
- -2t + 1,5t2) m
- (2t – 1,5t2) m
Soal No.3 (SBMPTN 2014)
Planet A mengitari sebuah bintang pada lintasan berbentuk lingkaran berjari-jari R dengan periode T. Jika planet b mengitari bintang yang sama ada lintasan lingkaran berjari-jari 4R, maka periode edar lanet B adalah …
- T/2
- 2T
- 4T
- 8T
- 16T
PEMBAHASAN :
Untuk menyelesaikan soal ini kita akan menggunkan hukum kepler III
T2 = R3![]()
![]()
![]()
![]()
T2 = 8T
Jawaban : D
Soal No.4 (SBMPTN 2014)
Sebuah kotak diletakkan pada bak mobil terbuka yang sedang mulai bergerak dengan percepatan 6 m/s2. Massa kotak adalah 40 kg. Jika koefisien gesekan statik dan kinetik antara lantai bak terbuka dan kotak berturut-turut adalah 0,8 dan 0,5 maka gaya gesekan yang diberikan lantai bak terbuka pada kotak adalah sebesar …
- 120 N
- 160 N
- 200 N
- 240 N
- 320 N
PEMBAHASAN :
kotak pada bak mobil mulai bergerak sehingga yang berlaku adalah gaya gesek statik.
Fs = µs N
Fs = µs mg
Fs = (0,8)(40)(10)
Fs = 320 N
Jawaban : E
Soal No.5 (UN 2014)
Seseorang dengan massa 60 kg berada di dalam lift yang bergerak ke bawah dengan percepatan 3 ms2. Jika percepatan gravitasi 10 ms2, gaya desakan kaki orang pada lantai lift adalah …
- 420 N
- 570 N
- 600 N
- 630 N
- 780 N
PEMBAHASAN :
Untuk menyelesaikan soal ini kita mengunakan hukum Newton II
∑F = ma
w – N = ma
N = mg – ma
N = m(g-a)
N = (60kg)(10-3) m/s2
N = 420 N
Jawaban : A
Soal No.6 (SBMPTN 2012)
Kedua ujung sebuah pegas memiliki tetapan pegas 50 N/m ditarik masing-masing dengan gaya sebesar 10 N yang saling berlawanan. Pertambahan panjang pegas tersebut adalah …
- 0,0 m
- 0,1 m
- 0,2 m
- 0,3 m
- 0,4 m
PEMBAHASAN :
Soal ini kita selesaikan dengan menggunakan Hukum Hooke
F = kΔx![]()
maka pertambahan panjang total yaitu
2Δx = 2 (0,2) = 0,4 M
Jawaban : E
Soal No.7 (UN 2013)
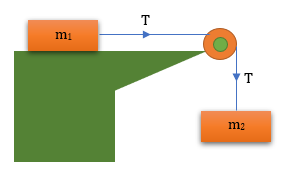
Benda m1 = 4 kg terletak di meja licin dan dihubungkan dengan benda m2 = 6 kg yang tergantung pada ujung mega. Benda m1 mula-mula ditahan kemudian dilepaskan hingga bergerak, maka tegangan tali T adalah…
- 96 N
- 72 N
- 40 N
- 24 N
- 15 N
PEMBAHASAN :
Untuk mengerjakan soal ini kita mengunakan Hukum Newton II
∑F = ma
w2 = (m1 + m2)a
60 = (4 + 6)kg a
a = 6 m/s2
∑F = m2a
w2– T = m2a
60-T = (6 kg)(6 m/s2)
T = 24 N
Jawaban : D
Soal No.8 (UN 2013)
Jika massa benda 2kg dan sudut kemiringan 30 serta percepatan gravitasi (g=9,8 ms-1) benda akan tetap meluncur. Nilai koefisien gesekan maksimum antara benda dengan bidang miring adalah …
PEMBAHASAN :
Untuk menyelesaikan soal ini kita akan menggunakan hukum Newton 1
∑F = 0
w sin α – fs = 0
w sin α = fs
w sin α = µs w cos α![]()
µs = tan α
µs= tan 30o
µs= ![]()
Jawaban : B
Soal No.9 (UN 2013)
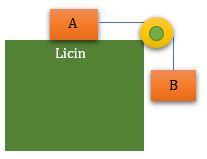
- 2,5 ms2
- 10 ms2
- 12 ms2
- 15 ms2
- 18 ms2
PEMBAHASAN :
Untuk menyelesaikan soal ini kita pakai hukum Newton II
∑F = m.a
Wb = (m1+m2)a
100 = (30+10)a
a = 2,5 ms-2
Jawaban : A
Soal No.10 (UN 2009)
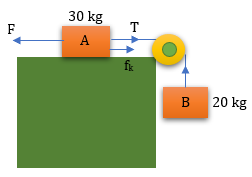
- 70 N
- 90 N
- 150 N
- 250 N
- 330 N
PEMBAHASAN :
Soal ini dikerjakan dengan menggunakan Hukum Newton II
∑F = m. a
(F-fk-wB) = (mA + mB)g
F-µk NA-wB = (30+20)(2)
F-µk mAg-mag=100
F-(0,1)(30)(10)=(20)(10)=100
F= 330 N
Jawaban : E
Soal No.11 (UN 2008)

- Benda diam
- Benda bergerak lurus beraturan
- Bergesekan dengan percepatan nol
- Bergerak dengan percepatan 2 ms2
- Bergerak dengan percepatan 5 ms2
PEMBAHASAN :
Penyelesain menggunakan Hukum Newton II. Karena gaya ke kanan lebih besar, benda bergerak ke kanan dan gaya geseknya ke kiri
∑F = ma
F2-F1-fk = ma
40-15-5 = 4a
20 = 4a
a = 5 ms2
Jawaban : E
Soal No.12 (UN 2013)
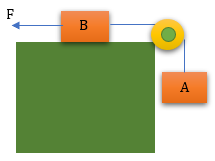
- 5 ms2
- 7,5 ms2
- 10 ms2
- 12,5 ms2
- 15 ms2
PEMBAHASAN :
Mengerjakan soal ini ingat Hukum Newton II
∑F = m.a
F-wA = (mA+mB)a
(40-20)N = (2+2)kg . a
a = 5 ms2
Jawaban : A
Soal No.13 (UN 2010)
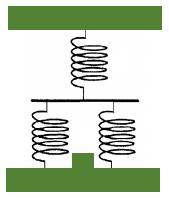
- 0,50
- 0,75
- 0,85
- 1,00
- 1,50
PEMBAHASAN :
Untuk pegas yang disusun paralel: Kp = 200 N/m + 200 N/m = 400 N/m
K total merupakan Penjumlahan dari pegas yang dihubungkan secara seri![]()
![]()
F = kΔx![]()
Δx = 0,75×10-2m = 0,75 cm
Jawaban : B
Soal No.14 (UN 2015)
Sebuah balok dengan berat W newton terletak pada saat t = 0 s, balok diam. Kemudian dari waktu t = 0 s sampai dengan t = 5 s balok didorong dengan gaya konstan F newton sejajar bidang datar sehingga balok bergerak dan baru berhenti pada t = 10 s. Jika koefisien gesek kinetik antara balok dan bidang datar adalah 0,2 maka….
- 5F = W
- 5F = 2W
- 2F = W
- 2F = 5W
- F = 5W
PEMBAHASAN :
Menentukan percepatan (a) pada t = 0 s sampai t = 5 s (diberi gaya sebesar F dan mengalami gaya gesek f)
ΣF = m.a1
F – f = m.a1![]()
Menentukan percepatan (a) pada t = 5 s sampai t = 10 s (hanya gaya gesek f yang bekerja)
ΣF = m.a2
f = m.a2![]()
Karena tidak ada perubahan percepatan maka
a1 = a2![]()
F = 2f
F = 2.(0,2. W)
F = 0,4 W
5F = 2W
Jawaban : B
Soal No.15 (SBMPTN 2012)
Keadaan di bawah ini yang menyebabkan besar gaya normal yang bekerja pada benda tidak sama dengan berat benda tersebut adalah….
- Pada kondisi benda diam di dasar kolam
- Benda diam di atas benda miring
- Benda berada di lift yang bergerak ke atas dengan percepatan tetap
- Benda di atas bidang datar, di tarik ke atas tali, tetapi tetap diam
PEMBAHASAN :
- Pada kondisi benda diam di dasar kolam, berlaku:

ΣF = 0
N + FA = w
N + FA – w = 0
N = w – FA
Maka N ≠ w
BENAR - Benda diam di atas bidang miring
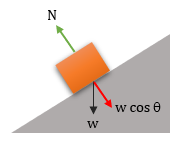
ΣF = 0
N – w cos θ = 0
N = w cos θ
Maka N ≠ w
BENAR - Benda berada di lift yang bergerak ke atas dengan percepatan tetap.
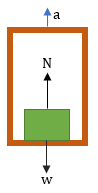
ΣF = ma
N – w = ma
N = w + ma
Maka N ≠ w
BENAR - Benda di atas bidang datar, di tarik ke atas tali, tetapi tetap diam.
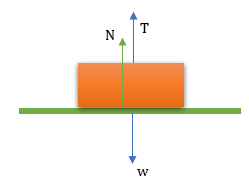
ΣF = 0
N + T= w
N = w – T
Maka N ≠ w
BENAR
Semua jawaban benar
Jawaban : E
Soal No.16 (UN 2011)
Perbandingan massa planet A dan B adalah 2 : 3 sedangkan perbandingan jari-jari planet A dan B adalah 1 : 2. Jika berat benda di planet A adalah w, maka berat benda tersebut di planet B adalah….
- 3/8 w
- 3/4 w
- 1/2 w
- 4/3 w
- 8/3 w
PEMBAHASAN :
Diketahui:
mA : mB = 2 : 3
RA : RB = 1 : 2
wA = w
Menentukan berat benda di planet B (wB) melalui perbandingan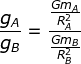
G dapat di coret karena merupakan tetapan, sehingga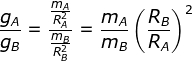
Masukan data yang diketahui ke persamaan tersebut.![]()
Karena berat benda (w) sebanding dengan percepatan gravitasi (g) di dalam persamaan w = m.g, maka![]()
![]()
![]()
Jawaban : A
Soal No.17 (UN 2010)
Seorang astronot ketika berada di permukaan bumi mengalami medan gravitasi sebesar g maka ketika berada pada ketinggian 1,5R dari permukaan bumi akan mengalami medan gravitasi sebesar….(R : jari-jari bumi)
PEMBAHASAN :
Diketahui:
h = 1,5 R
Menentukan percepatan gravitasi pada ketinggian 1,5 R melalui perbandingan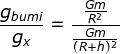
Karena G tetapan dan tidak ada perbedaan massa, maka G dan m dapat di coret sehingga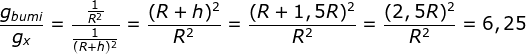
maka ![]()
Jawaban : C
Soal No.18 (UN 1998)
Sistem pada gambar berikut ini dalam keadaan seimbang dan benda A tepat akan bergerak. Koefisien gesek statis A dengan lantai adalah μs. Persamaan gaya dalam arah mendatar yang benar adalah…
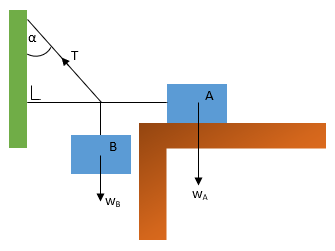
- μs wA = T cos α
- μs wA = T sin α
- μs wA + wA cot α = 0
- μs wA – T cos 45º = 0
- μs (wA – wB) = T cos α
PEMBAHASAN :
Perhatikan gambar berikut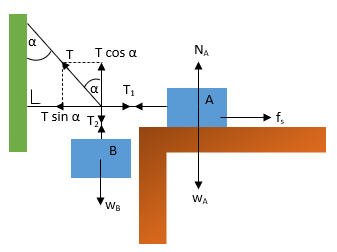
Pada arah mendatar atau sumbu X, berlaku:
ΣFx = 0
T1 – fs = 0
T1 = fs
T1 = μs wA
ΣFx = 0
T1 – T sin α = 0
μs wA – T sin α = 0
μs wA = T sin α
Jawaban : B
Soal No.19 (SBMPTN 2011)
Perhatikan gambar berikut!
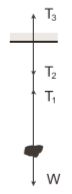
Sebuah batu digantung dengan seutas tali pada langit-langit suatu ruang. Gaya oleh tali pada langit-langit T2 merupakan reaksi bagi tegangan tali T1.
SEBAB
Gaya-gaya T1 dan T2 sama besar, tetapi berlawanan arah.
PEMBAHASAN :
Gaya tali T2 merupakan reaksi bagi tegangan tali T3, bukan reaksi bagi tegangan tali T1. T1 merupakan reaksi bagi gaya berat w. Pernyataan Salah
Besar gaya T2 dan T1 sama besar namun berlawanan arah. Alasan benar
Jawaban : D
Soal No.20 (SNMPTN 2011)
Pada benda diam, resultan gaya yang bekerja pada benda tersebut adalah nol.
SEBAB
Pada benda diam tidak ada satupun gaya yang bekerja padanya
PEMBAHASAN :
Sesuai dengan konsep hukum I Newton ΣF = 0, pada benda diam resultan gaya yang bekerja pada benda adalah nol. Pernyataan Benar
Pada benda diam ada gaya yang bekerja pada benda, gaya berat, gaya normal yang jika dijumlahkan gaya keseluruhan pada benda diam akan bernilai nol. Alasan salah
Jawaban : C
Soal No.21 (SNMPTN 2008)
Dua balok masing-masing bermassa m dihubungkan dengan seutas tali dan ditempatkan pada bidang miring licin menggunakan sebuah katrol. Jika massa tali dan katrol diabaikan dan sistem bergerak ke kiri maka besar tegangan tali adalah…
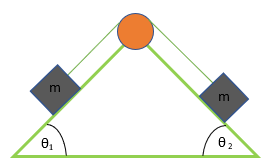
- ½mg(sin θ1 – sin θ2)
- ½mg(sin θ1 + sin θ2)
- mg(sin θ1 – sin θ2)
- mg(sin θ1 + sin θ2)
- 2mg(sin θ1 – sin θ2)
PEMBAHASAN :
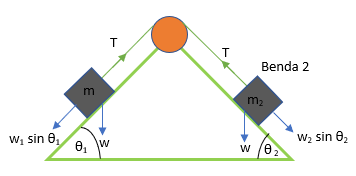
ΣF = ma
Menentukan besar tegangan tali dengan meninjau benda 2
ΣF = m2a
w2 sin θ2 – T = m2a
![]()
T = ½mg(sin θ1 + sin θ2)
Jawaban : B
Soal No.22 (SPMB 2004)
Sebuah helikopter bermassa 300 kg bergerak vertikal ke atas dengan percepatan 2 m/s2. Seorang tentara bermassa 60 kg memanjat tali yang menjulur dari helikopter dengan kecepatan tetap 1 m/s relatif terhadap helikopter. Gaya tegangan tali saat itu adalah…
- 600 N
- 660 N
- 720 N
- 780 N
- 3.600 N
PEMBAHASAN :

ΣF = ma
T – worang = morang a
T = worang + morang a
T = 60. 10 + 60 . 2 = 720 N
Jawaban : C
Soal No.23 (SPMB 2002)
Pada gambar berikut ini, sistem dalam keadaan setimbang. Perbandingan massa A dan massa B adalah…

- 1 :
- 1 : 2
 : 1
: 1- 2 : 1
- 3 : 1
PEMBAHASAN :
Untuk menentukan perbandingan massa A dan B digunakan penurunan rumus untuk benda yang digantung dengan seutas tali melalui katrol.
g dapat dicoret sehingga:
Maka:
Jawaban : A
Soal No.24 (UMPTN 2001)
Gaya (F) sebesar 12 N bekerja pada sebuah benda yang massanya m1, menyebabkan percepatan m1 sebesar 8 ms-2. Jika F bekerja pada benda yang bermassa m2, maka percepatan yang ditimbulkan adalah 2 ms-2. Jika F bekerja pada benda yang bermassa m1 + m2, maka percepatan benda ini adalah…
- 1,2 ms-2
- 1,6 ms-2
- 2,4 ms-2
- 3,0 ms-2
- 3,6 ms-2
PEMBAHASAN :
Diketahui:
F = 12 N
percepatan (a) pada m1 = 8 ms-2
percepatan (a) pada m2 = 2 ms-2
F = m1. a
12 = m1. 8
m1 = 12/8 = 1,5 kg
Menentukan m2
F = m2. a
12 = m2. 2
m1 = 12/2 = 6 kg
Maka m1 + m2 = 1,5 + 6 = 7,5 kg
Menentukan percepatan saat benda bermassa m1 + m2
F = (m1 + m2) .a
12 = 7,5 . a
a = 12/7,5 = 1,6 ms-2
Jawaban : B
Soal No.25 (UMPTN 2000)
Balok yang beratnya w ditarik sepanjang permukaan mendatar dengan kelajuan v oleh gaya F yang bekerja pada sudut θ terhadap horizontal. Besarnya gaya normal yang bekerja pada balok oleh permukaan adalah…
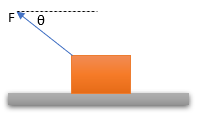
- w + F cos θ
- w + F sin θ
- w – F sin θ
- w – F cos θ
- w
PEMBAHASAN :
Tinjau benda:
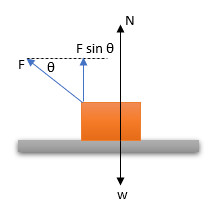
ΣF = 0
N + F sin θ – w = 0
N = w + F sin θ
Jawaban : B
Soal No.26 (UMPTN 1999)
Diketahui:
TA = T
RA = p
RB = q
Untuk menentukan periode revolusi planet B menggunakan perbandingan kedua planet menggunakan Hukum III Kepler
Soal No.27 (UMPTN 1997)
Sebuah satelit bumi mengorbit setinggi 3.600 km di permukaan bumi. Jika jari-jari bumi 6.400 km dan gerak satelit dianggap melingkar beraturan, maka kelajuan (dalam km/s) adalah….
- 6,4
- 64
- 640
- 6400
- 64000
PEMBAHASAN :
Diketahui:
R = 6.400 km
h = 3.600 km
r = R + h = 6.400 + 3.600 = 10.000 km
Menentukan kelajuan satelit
Soal No.28 (UMPTN 1997)
Tinjaulah sebuah satelit yang diluncurkan ke atas dengan laju awal v! Jika gesekan dengan udara diabaikan, massa bumi = M, massa satelit m , dan jari-jari bumi = R, agar satelit tidak kembali ke bumi, v2 berbanding lurus dengan….
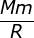
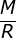
- M2 R
- MR
- MmR
PEMBAHASAN :
Persamaan kecepatan lepas satelit dituliskan sebagai berikut:
atau
Semoga Bermanfaat