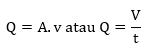Rangkuman Fluida Dinamis, Contoh Soal & Pembahasan

1. Fluida dianggap tidak kompresibel.
2. Fluida dianggap bergerak tanpa gesekan walaupun ada gerakan materi (tidak mempunyai kekentalan).
3. Aliran fluida adalah aliran stasioner, yaitu kecepatan dan arah gerak partikel fluida yang melalui suatu titik tertentu selalu tetap.
   
4. Tak bergantung waktu (tunak), artinya kecepatannya konstan pada titik tertentu dan membentuk aliran laminer (berlapis)

DEBIT

Yaitu Volume fluida tiap satuan waktu yang mengalir dalam pipa. Dirumuskan sebagai berikut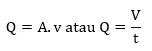

Keterangan :
Q : debit (m³/s)
V : volume fluida (m³)
T : waktu (s)
A : luas (m²)
V : kecepatan (m/s)

PERSAMAAN KONTINUITAS

Persamaan kontinuitas berbunyi “pada fluida yang tak termampatkan, hasil kali antara kelajuan aliran fluida dalam suatu wadah dengan luas penampang wadah selalu konstan”.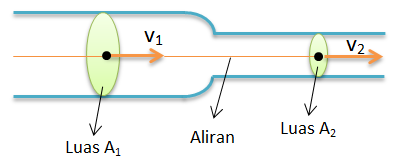

Jika suatu wadah memiliki penampang yang berbeda maka menurut persamaan kontinuitas berlaku
Q₁ = Q₂
A₁.v₁ = A₂. v₂
Keterangan :
Q₁ = debit ketika masuk (m³/s)
Q₂ = debit ketika keluar (m³/s)
A₁ = luas penampang 1 (m²)
A₂ = luas penampang 2 (m²)
v₁ = kecepatan fluida ketika masuk (m/s)
v₂ = kecepatan fluida ketika keluar (m/s)

Persamaan Bernoulli

Menurut persamaan ini, besaran p + ρgh + ½ ρv₁² memiliki nilai yang sama pada setiap titikdalam aliran fluida, sesuai dengan gambar berikut:

Bila dituliskan dalam suatu persamaan yaitu sebagai berikut :
p₁ + ρgh₁ + ½ ρv₁² = p₂ + ρgh₂ + ½ ρv₂²
Keterangan :
p₁, p₂ = tekanan di titik 1 dan 2 (N/m²)
v₁, v₂ = kecepatan aliran di titik 1 dan 2 (m/s)
h₁, h₂ = ketinggian di titik 1 dan 2 (m)
ρ = massa jenis fluida (kg/m³)
g = percepatan gravitasi (m/s²)

Penggunaan Persamaan BERNOULLI

Gaya angkat pesawat

Pesawat terbang dapat terangkat ke udara karena kecepatan udara pada sayap bagian atas lebih besar dibandingkan dengan kecepatan udara pada sayap bagian bawah. Akibatnya tekanan bagian atas lebih kecil dibandingkan tekanan bagian bawah. Ditunjukan melaui gambar berikut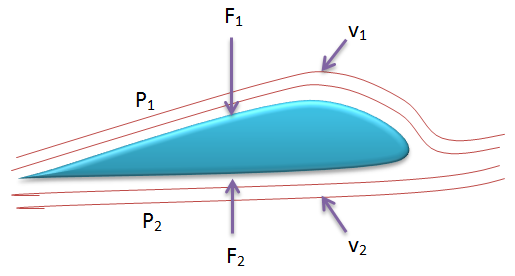

F₁ – F₂ = ½ ρA (v₂²-v₁²)
Keterangan
F₁ – F₂ = gaya angkat pesawat terbang (N)
P₁ = tekanan pada sayap bagian bawah (N/m²)
P₂ = tekanan pada sayap bagian atas (N/m²)
A = luas penampang sayap (m²)
v₁ = kecepatan udara sayap bagian atas (m/s)
v₂ = kecepatan udara sayap bagian bawah (m/s)
ρ = massa jenis (kg/m)

Venturimeter tanpa manometer

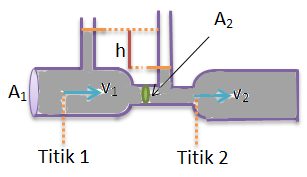
kelajuan pada luas penampang A₁ yaitu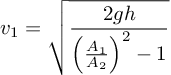

keterangan :
v₁ = kelajuan fluida pada penampang 1
g = percepatan gravitasi (m/s2)
h = perbedaan ketinggian pada fluida (m)
A₁ = luas penampang 1
A₂ = luas penampang 2

Venturimeter dengan manometer

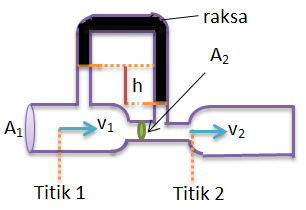
Kelajuan pada luas penampang A₁ sebagai berikut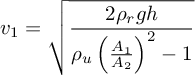

Keterangan :
v₁ = kelajuan fluida pada penampang 1
g = percepatan gravitasi (m/s2)S
h = perbedaan ketinggian pada fluida (m)
A₁ = luas penampang 1 (m2)
A₂ = luas penampang 2 (m2)
ρ_r = massa jenis raksa (kg/m3)
ρ_u = massa jenis udara (kg/ms3)
v₂ = kecepatan udara sayap bagian bawah (m/s)
P = massa jenis (kg/m3)

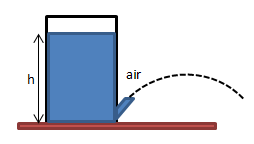
Tangki berlubang

Keterangan :
v = kecepatan semburan (m/s)
g = percepatan gravitasi (m/s²)
h = tinggi lubang dari permukaan air (m)

waktu yang dibutuhkan semburan air mencapai tanah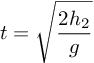

keterangan :
t = waktu yang dibutuhkan air mencapai tanah (s)
g = percepatan gravitasi (m/s²)
h₂ = ketinggian lubang diukur dari permukaan tanah (m)

jarak jangkauan air (x)

keterangan :
h = tinggi lubang dari permukaan air (m)
h₂ = ketinggian lubang diukur dari permukaan tanah (m)

Soal No.1 (UN 2012)

suatu zat cair dialirkan melalui pipa seperti tampak pada gambar berikut.

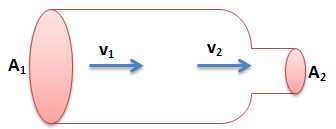
Jika luas penampang A₁ = 8 cm² , A₂ = 2cm², dan laju zat cair v₂ = 2m/s, maka besar v₁ adalah….

1. 0,5 m/s
2. 1,0 m/s
3. 1,5 m/s
4. 2,0 m/s
5. 2,5 m/s

PEMBAHASAN :
Untuk menghitung besarnya v₁ kita akan menggunakan persamaan kontinuitas
Q₁ = Q₂
A₁.v₁ = A₂. v₂
8. v₁= 2. 2

Jawaban : A

Soal No.2 (UMPTN 1995)

Air mengalir pada suatu pipa yang diameternya berbeda dengan perbandingan 1: 2. Jika kecepatan air yang mengalir pada bagian pipa yang besar sebesar 40 m/s, maka besarnya kecepatan air pada bagian pipa yang kecil sebesar…. m/s

1. 20
2. 40
3. 80
4. 120
5. 160

PEMBAHASAN :
Diketahui diameter pipa kecil : diameter pipa besar = 1 : 2
v₂ = 40 m/s
Untuk menghitung besarnya v₁ kita akan menggunakan persamaan kontinuitas
Q₁ = Q₂
A₁.v₁ = A₂. v₂
Luas penampang dihitung dari luas lingkaran dimana A = 1/4.πd², sehingga:
1/4.πd₁². v₁=1/4.πd₂². v₂
(1)².v₁= (2)². 40 m/s

Jawaban : E

Soal No.3 (UN 2002)

Pipa berjari-jari 15 cm disambung dengan pipa lain yang berjari-jari 5cm. Keduanya dalam posisi horizontal. Apabila kecepatan aliran air pada pipa besar adalah 1 m.s^-1 pada tekanan 10⁵ N.m^-2, maka tekanan pada pipa yang kecil (massa jenis air 1 gr.cm^-3) adalah….

1. 10.000 N m^-2
2. 15.000 N m^-2
3. 30.000 N m^-2
4. 60.000 N m^-2
5. 90.000 N m^-2

PEMBAHASAN :
Untuk menghitung besarnya kecepatan pada pipa kecil (v₂) kita akan menggunakan persamaan kontinuitas
Q₁ = Q₂
A₁.v₁ = A₂. v₂
Karena lingkaran untuk menentukan luas penampang, menggunakan rumus A = πr²
πr₁². v₁= πr₂². v₂
(15)².1 = (5)². v₂

Untuk menghitung tekanan di pipa kecil (P₂) kita akan menggunakan Persamaan Bernoulli:
p₁ + ρgh₁ + ½ ρv₁² = p₂ + ρgh₂ + ½ ρv₂²
Karena posisi keduanya horizontal maka nilai h₁ dan h₂ = 0, maka
P₁ + ½ ρv₁² = P₂ + ½ ρv₂²
P₂ = P₁+ ½ ρ(v₁²-v₂²)
P₂ = 10⁵ + 1/2. 10³. (1²– 9²)
P₂ = 100.000 – 40.000
P₂ = 60.000 N.m^-2
Jawaban : D

Soal No.4 (SIMAK UI 2011)

Fluida ideal mengalir melalui pipa mendatar dengan luas penampang A m², kemudian fluida mengalir melalui dua pipa yang luas penampangnya lebih kecil seperti gambar.

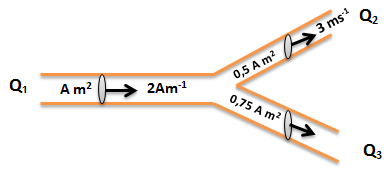
Kecepatan fluida pada pipa yang luas penampangnya 0,75 A m² adalah….

1. 0,5 m/detik
2. 2/3 m/detik
3. 1,5 m/detik
4. 2 m/detik
5. 2,5 m/detik

PEMBAHASAN :
Untuk menyelesaikan soal ini kita menggunakan persamaan kontinuitas
Q₁ = Q₂ + Q₃
A₁.v₁ = A₂. v₂ + A₃. v₃
A. 2 = 0,5 A. 3 + 0,75 A. v₃
v₃ = 2/3 m/s
Jawaban : B

Soal No.5 (UN 2011)

Sayap pesawat terbang dirancang agar memiliki gaya angkat ke atas maksimal, seperti gambar jika v adalah kecepatan aliran udara dan P adalah tekanan udara maka sesuai dengan azas bernoulli rancangan tersebut dibuat agar…..

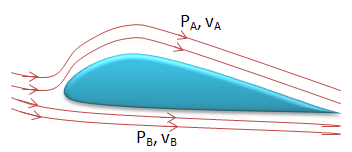
1. V_A > V_B sehingga PA > P_B
2. V_A > V_B sehingga PA < P_B
3. V_A < V_B sehingga PA < P_B
4. V_A < V_B sehingga PA > P_B
5. V_A > V_B sehingga PA = P_B

PEMBAHASAN :
Menurut Persamaan Bernoulli jika kecepatan fluida makin besar maka tekanannya makin kecil. Menurut gambar agar sayap pesawat terangkat maka perlu P_B > P_A maka v_A > v_B
Jawaban : B

Soal No.6 (UN 2007)

Sebuah tabung berisi penuh zat cair (ideal). Pada dindingnya sejauh 20 cm dari permukaan atas terdapat lubang kecil (jauh lebih kecil dari penampang tabung) sehingga zat cair memancar (terlihat seperti pada gambar)
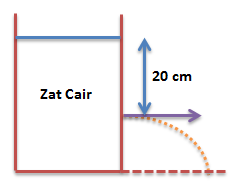Besar kecepatan pancaran air tersebut dari lubang kecil….

1. 1,0 M/S
2. 2,0 M/S
3. 3,0 M/S
4. 5,0 M/S
5. 5,5 M/S

PEMBAHASAN :
Diketahui h = 20 cm = 0,2 m
Untuk menentukan kecepatan pancaran air kita menggunakan rumus:


Jawaban : B

Soal No.7 (UMPTN 1992)

Air terjun setinggi 8 m dengan debit 10 m³/s dimanfaatkan untuk memutar generator listrik mikro. Jika 10% energi air berubah menjadi energi listrik dan g = 10 m/s² daya keluaran generator listrik adalah….

1. 70 Kw
2. 75 Kw
3. 80 kw
4. 90 Kw
5. 95 Kw

PEMBAHASAN :

Diketahui η = 10%, g = 10 m/s², ρ_air = 1000 g/L, Q = 10 m³/s, h = 8 m
Menghitung daya dari air terjun menggunakan rumus:
P = ηρQgh
P = 10%.1000.10.10.8
P = 80.000 W = 80kW
Jawaban : C

Soal No.8 (UN 1990)

Air mengalir melalui pipa yang bentuknya seperti pada gambar.

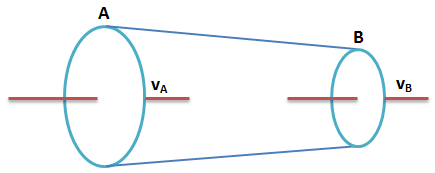
Bila diketahui luas penampang di A dua kali penampang di B maka vA/vA sama dengan…..

1. 1/4
2. 1/2
3. 1
4. 2
5. 4

PEMBAHASAN :
Untuk menyelesaikan soal ini kita menggunakan persamaan kontinuitas
Q_A = Q_B
A_A.v_A = A_B. v_B


Jawaban : B

Soal No.9 (UN 2008)

Gambar berikut ini menunjukkan peristiwa kebocoran pada tangki air.

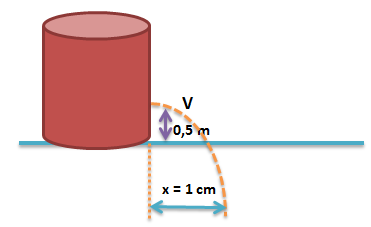
Kecepatan (v) air yang keluar dari lubang adalah….

PEMBAHASAN :
menghitung terlebih dahulu waktu yang diperlukan air sampai tanah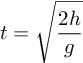


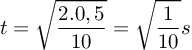
diketahui x = 1 m, untuk menghitung v digunakan rumusan: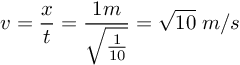

Jawaban : B

Soal No.10 (UN 2013)

Sebuah bak penampung berisi air setinggi 1 meter (g = 10 m/s²) dan pada dinding terdapat lubang kebocoran (lihat gambar).

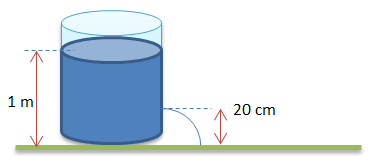
Kelajuan air yang keluar dari lubang tersebut adalah….

1. 1 m/s
2. 2 m/s
3. 4 m/s
4. 8 m/s
5. 10 m/s

PEMBAHASAN :
Diketahui h = 1 m – 0,2 m = 0,8 m
untuk menghitung kelajuan air yang keluar menggunakan rumus: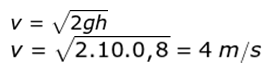

Jawaban : C

Soal No.11 (UN 2012)

Perhatikan gambar penampang pipa berikut!

Air mengalir dari pipa A ke B terus ke C. Perbandingan luas penampang A dengan penampang C adalah 8 : 3. Jika kecepatan aliran di penampang A adalah v maka kecepatan aliran pada pipa C adalah….

1. 
2. 
3. v
4. 
5. 8 v

PEMBAHASAN :
Berdasarkan asas kontinuitas berlaku
Q_A = Q_C
A_A v_A = A_C v_C
Dari soal diketahui A_A : A_A = 8 : 3 dengan vA = v, maka vC

Jawaban : C

Soal No.12 (UMPTN 1989)

Air terjun setinggi 10 m dengan debit 50 m³/s dimanfaatkan untuk memutar turbin yang menggerakkan generator listrik. Jika 25% energi air dapat berubah menjadi energi listrik dan g = 10 m/s² maka daya keluaran generator adalah….

1. 0,9 MW
2. 1,10 MW
3. 1,25 MW
4. 1,30 MW
5. 1,50 MW

PEMBAHASAN :
Menentukan daya keluaran generator
P_out = ηρQgh
P_out = 25%. 1000. 50.10.10
P_out = 1250000 W = 1,25 MW
Jawaban : C

Soal No.13 (UN 1993)

Kecepatan fluida ideal pada penampang A₁ adalah 20 m/s. Jika luas penampang A₁ = 20 cm² dan A₂ = 5 cm² maka kecepatan fluida pada penampang A₂ adalah….

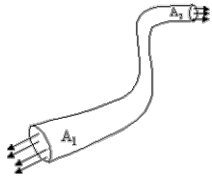
1. 1 m/s
2. 5 m/s
3. 20 m/s
4. 80 m/s
5. 100 m/s

PEMBAHASAN :
Berdasarkan asas kontinuitas berlaku
Q₁ = Q₂
A₁ v₁ = A₂ v₂
Diketahui v₁ = 20 m/s, A₁ = 20 cm² dan A₂ = 5 cm² maka v₁

Jawaban : D

Soal No.14 (PP 1980)

Sebuah pipa silindris yang lurus mempunyai dua macam penampang, masing-masing dengan luas 200 mm² dan 100 mm². Pipa tersebut diletakkan secara horizontal, sedangkan air di dalamnya mengalir dari penampang besar ke penampang kecil. Apabila kecepatan arus di penampang besar adalah 2 m/s maka kecepatan arus di penampang kecil…

1. ¼ m/s
2. ½ m/s
3. 1 m/s
4. 2 m/s
5. 4 m/s

PEMBAHASAN :
Berdasarkan asas kontinuitas berlaku
Q₁ = Q₂
A₁ v₁ = A₂ v₂
Diketahui v₁ = 2 m/s, A₁ = 200 mm² dan A₂ = 100 mm² maka v₂

Jawaban : E

Soal No.15 (UN 2014)

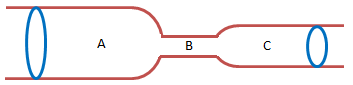
Pada gambar, air dipompa dengan kompresor bertekanan 120 kPa memasuki pipa bagian bawah (I) dan mengalir ke atas dengan kecepatan 1 m/s, (g = 10 m/s² dan massa jenis air 1000 kg/m³). Tekanan air pada bagian atas (II) adalah…

1. 52,5 kPa
2. 67,5 kPa
3. 80,0 kPa
4. 92,5 kPa
5. 107,5 kPa

PEMBAHASAN :
Menentukan v_II dari persamaan Kontinuitas
Q_I = Q_II
A_I v_I = A_II v_II
Diketahui v₁ = 1 m/s, r_I = 12 cm dan r_II = 6 cm maka v₂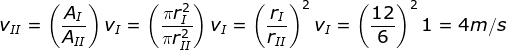

Menentukan tekanan air pada bagian atas (II) melalui persamaan Bernoulli
P_I + ½ρv_I² + ρgh_I = P_II + ½ρv_II² + ρgh_II
12 x 10⁴ + ½.10³.(1)² + 10³ (10)(0) = P_II + ½.10³.(4)² + 10³ (10)(2)
P_II = 120.500 – 28.000
P_II = 92.500 Pa = 92,5 kPa
Jawaban : D

Soal No.16 (UMPTN 1996)

Air terjun setinggi 20 m digunakan untuk pembangkit listrik tenaga air (PLTA). Setiap detik air mengalir 10 m³ . Jika efisiensi generator 55% dan percepatan gravitasi g = 10 m/s², daya rata-rata yang dihasilkan adalah…kW

1. 110
2. 1100
3. 2200
4. 2500
5. 5500

PEMBAHASAN :
Menentukan daya keluaran yang dihasilkan
P_out = ηρQgh = (55%)(1000)(10)(10)(20) = 1100 kW
Jawaban : B

Soal No.17 (UN 2013)

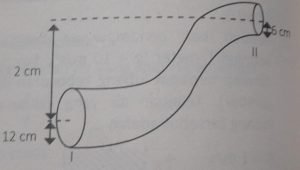
Sebuah tangki dipasang kran pada dindingnya tampak seperti gambar dan diisi air.

Kecepatan pancaran air saat kran dibuka adalah….

1. 2,5 m/s
2. 3,4 m/s
3. 5,0 m/s
4. 8,0 m/s
5. 12,5 m/s

PEMBAHASAN :
Diketahui:
g = m/s²
tinggi pancaran ke permukaan air (h) = 1,25 m
Menentukan kecepatan pancaran air (v) menggunakan rumusan

Jawaban : B

Soal No.18 (Tes ITB 1976)

Pesawat terbang dapat mengangkasa karena…

1. perbedaan tekanan dan aliran-aliran udara
2. pengaturan titik berat pesawat
3. gaya angkat dari mesin pesawat
4. perubahan momentum dari pesawat
5. berat pesawat yang lebih kecil daripada berat udara yang dipindahkan

PEMBAHASAN :
Pesawat terbang dapat mengangkasa akibat adanya perbedaan tekanan dan aliran-aliran udara yang dijelaskan oleh Hukum Bernoulli yang menjelaskan kecepatan udara pada sayap bagian atas lebih besar dibandingkan dengan kecepatan udara pada sayap bawah sehingga tekanan bagian atas sayap akan menjadi lebih kecil dibanding tekanan sayap bagian bawah.
Jawaban : A

Soal No.19 (UN 2013)

Perhatikan alat-alat berikut!

1. Pompa hidraulik
2. Karburator
3. Venturimeter
4. Termometer

Alat-alat yang prinsip kerjanya berdasarkan hukum Bernoulli adalah….

1. 1 dan 2
2. 1 dan 3
3. 1 dan 4
4. 2 dan 3
5. 2 dan 4

PEMBAHASAN :
Alat yang menggunakan prinsip kerja berdasarkan hukum Bernoulli adalah karburator dan venturimeter. Sedangkan pompa hidraulik bekerja berdasarkan hukum pascal. Termometer bekerja berdasarkan hukum Archimides
Jawaban : D

Soal No.20 (SIMAK UI 2009)

Saat ketinggian pesawat bertambah, tekanan udara di bawah sayap pesawat terbang lebih besar daripada tekanan udara di atas permukaan sayap.

SEBAB

Kecepatan aliran udara di atas permukaan sayap lebih besar daripada kecepatan udara di bawah sayap.

PEMBAHASAN :
Pada pesawat terbang, agar mengangkasa maka kecepatan udara pada sayap bagian atas lebih besar dibandingkan dengan kecepatan udara pada sayap bawah sehingga tekanan bagian atas sayap akan menjadi lebih kecil dibanding tekanan sayap bagian bawah. Maka, pernyataan benar dan alasannya juga benar dan saling berhubungan
Jawaban : A

Soal No.21 (UN 2004)

Perhatikan gambar berikut ini!

Jika luas penampang pipa A = 10 cm² dan pipa B = 4 cm². Kecepatan aliran air pada pipa B, jika kecepatan aliran air pada pipa A = 10 m/s, maka kecepatan pada pipa B adalah….(m/s)

1. 25
2. 20
3. 15
4. 10
5. 5

PEMBAHASAN :
Sesuai asas kontinuitas
Q_A = Q_B
A_A v_A = A_B v_B
Diketahui v_A = 10 m/s, A_A = 10 cm² dan A_B = 4 cm² maka v_B

Jawaban : A

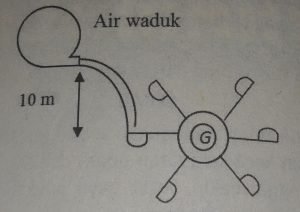
Soal No.22 (UMPTN 1999)

Pada gambar di atas, G adalah generator 1.000 W yang digerakkan degan kincir air. Generator hanya menerima energi sebesar 80% dari energi air. Jika generator dapat bekerja normal, debit air yang sampai ke kincir adalah….

1. 12,5 L/s
2. 25 L/s
3. 27,5 L/s
4. 125 L/s
5. 250 L/s

PEMBAHASAN :
Diketahui:
P_out = 1.000 W
η = 80%
h = 10 m
g = 10 m/s²
Menentukan debit air (Q)
P_out = ηρQgh

Jawaban : A

Soal No.24 (UN 2001)

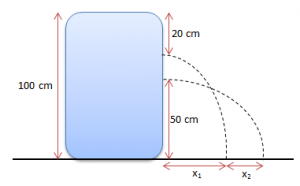
Sebuah tabung berisi zat cair (ideal). Pada dindingnya terdapat dua lubang kecil (jauh lebih kecil dari penampang tabung) sehingga zat cair memancar (terlihat seperti pada gambar).

Perbandingan antara x₁ dan x₂ adalah….

1. 2 : 3
2. 3 : 5
3. 2 : 5
4. 4 : 5
5. 3 : 4

PEMBAHASAN :
Menentukan perbandingan jarak jangkauan x₁ dengan x₂ menggunakan rumusan:

Keterangan:
x = jangkauan air
h₁ = tinggi lubang dari permukaan air
h₂ = tinggi lubang dari permukaan tanah
x₁ h₁ nya adalah 20 cm dan h₂ nya adalah 80 cm
x₂ h₁ nya adalah 50 cm dan h2 nya adalah 50 cm
maka perbandingannya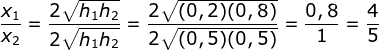

atau
x₁ : x₂ = 4 : 5
Jawaban : D

Soal No.25 (SIMAK UI 2011)

Sebuah pipa dengan luas penampang 616 cm² dipasang keran berjari – jari 3,5 cm di salah satu ujungnya. Jika kecepatan zat cair di pipa adalah 0,5 m/s. Maka dalam waktu 5 menit volume zat cair yang keluar dari keran adalah … m³

1. 10,2
2. 9,24
3. 8,29
4. 6,72
5. 5,2

PEMBAHASAN :
Diketahui:
A₁ = 616 x 10^-4 m²
r₂ = 3,5 cm maka A₂ = πr² = 3,14x(3,5)² = 12,25 cm²
v₁ = 0,5 m/s
t = 5 menit = 300 detik
Menentukan Volume zat cair yang keluar
Sesuai asas kontinuitas
Q₁ = Q₂
Q₁ = Q₂ = A₁.v₁ = 616 x 10^-4.(½) = 308 x 10^-4 m³/s

V = Qt
V = 308 x 10^-4. 3 x 10²
V = 924 x 10²
V = 9,24 m³
Jawaban : B

Soal No.26 (SBMPTN 2016)

Minyak (ρ = 0,8 x 10³ kg/m³) mengalir melewati pipa mendatar yang makin mengecil. Pada ujung pipa besar memiliki kelajuan 3,0 m/s. Perbedaan tekanan antara kedua ujung pipa adalah 2,8 kPa. Kelajuan minyak di ujung pipa yang kecil adalah … m/s

1. 2,5
2. 3,0
3. 3,5
4. 4,0
5. 4,5

PEMBAHASAN :
Diketahui:
Perbedaan tekanan (P₁ – P₂) = 2,8 kPa = 2800 Pa
Massa jenis (ρ) = 0,8 x 10³ kg/m³
v₁ = 3,0 m/s
Menentukan kelajuan minyak di ujung pipa kecil melalui persamaan Bernoulli
P₁ + ½ρv₁² + ρgh₁ = P₂ + ½ρv₂² + ρgh₂
Karena mendatar maka h₁= h₂, sehingga:
P₁ + ½ρv₁² = P₂ + ½ρv₂²
P₁ – P₂ + ½ρv₁² = ½ρv₂²
2800 + ½.800.9 = ½.800. v₂²
2800 + 3600 = 400. v₂²
v₂² = 16
v₂ = 4 m/s
Jawaban : D

Soal No.27 (SBMPTN 2016)

Ujung sebuah pipa silinder jari –jari 1,5 cm. Air (ρ = 1 x 10³ kg/m³) mengalir dengan laju tetap 7,0 m/s. Laju aliran massa yang meninggalkan pipa adalah … kg/s

1. 7000
2. 48
3. 7,0
4. 4,9
5. 2,5

PEMBAHASAN :
Diketahui:
r = 1,5 cm = 1,5 x 10^-2 m
ρ = 1 x 10³ kg/m³
v = 7,0 m/s
Menentukan laju aliran massa yang meninggalkan pipa
m = Aρv
m = πr² ρ v
m = (3,14)(2,25×10^-4)(1000)(7)
m = 4,94
m ≈ 4,9 kg/s
Jawaban : D

Soal No.28 (SBMPTN 2016)

Air dalam bak setinggi 0,2 m terletak 5 m di atas permukaan tanah.

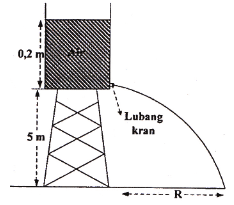
Di dasar bak terdapat lubang keran kecil sehingga air memancar keluar dan jatuh di permukaaan tanah pada jarak R. Jika g = 10 m.s^-2 nilai R adalah…

1. 2 meter
2. 5 meter
3. 7 meter
4. 10 meter
5. 15 meter

PEMBAHASAN :
Diketahui:
h₁ = 0,2 m
h₂ = 5 m
Menentukan jarak jangkauan air (R)

Jawaban : A

Soal No.29 (SBMPTN 2016)

Air (ρ = 1 x 10³ kg/m³) mengalir menuruni bukit melewati pipa dengan diameter 1,5 cm. kelajuan air di puncak bukit adalah 7,2 m/s. Jika ketinggian bukit adalah 9,5 m, maka kerapatan energi potensial (energi per satuan volume),pada puncak bukit relatif terhadap kaki bukit adalah …

1. 9,9 x 10⁴  J/m³
2. 9,7 x 10⁴  J/m³
3. 9,5 x 10⁴  J/m³
4. 7,2 x 10⁴  J/m³
5. 7,0 x 10⁴  J/m³

PEMBAHASAN :
Diketahui:
ρ = 1 x 10³ kg/m³
d₁ = 1,5 cm
v₁= 7,2 m/s
h₁ = 9,5 m
Menentukan kerapatan energi potensial

Jawaban : C

Soal No.30 (SBMPTN 2016)

Sebuah tangki air pada bagian bawahnya terdapat lubang sehingga air memancar keluar membentuk sudut 60° seperti pada gambar. Jika jarak pancarnya  cm dan , tinggi air (h) dalam tangki adalah…

1. 20 cm
2. 80 cm
3. 8√3 cm
4. 128 cm
5. 160 cm

PEMBAHASAN :
Diketahui:
x =  cm =
g = 10 m/s²
θ = 60^o
Menentukan kecepatan air
Karena air yang keluar merupakan gerak parabola, maka:



v_o² = 16
v_o = v =

16 = 20h

Jawaban : B