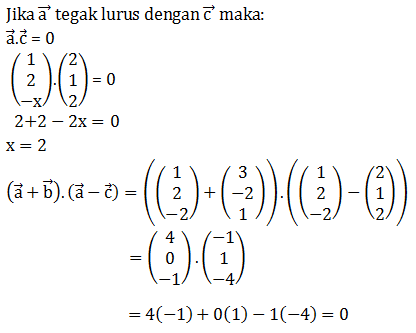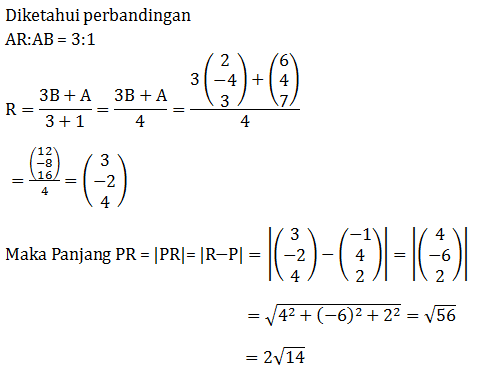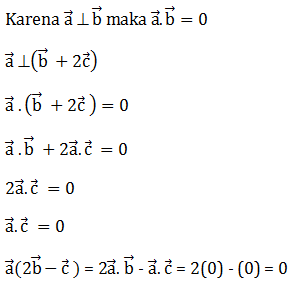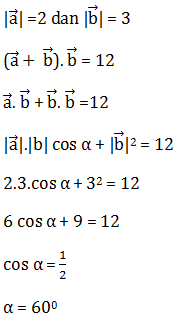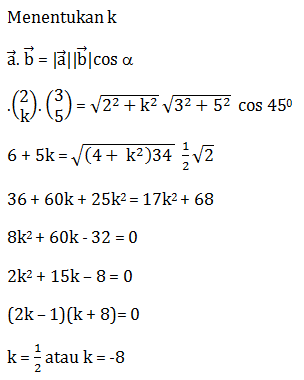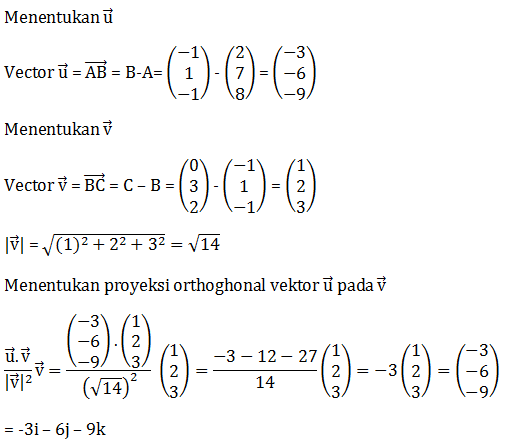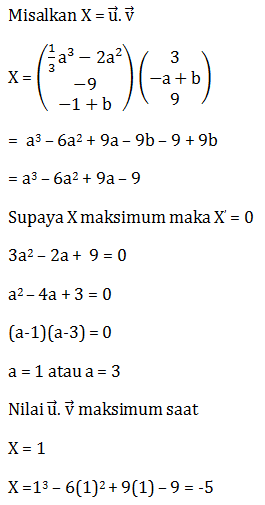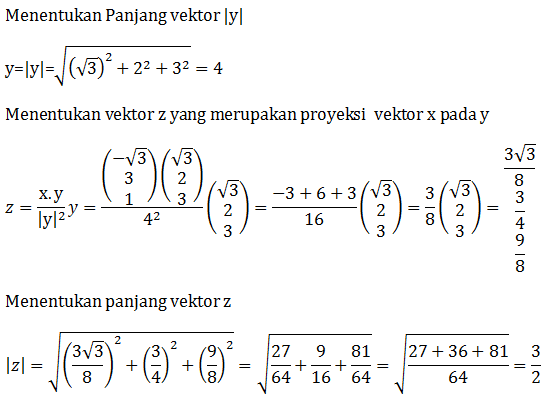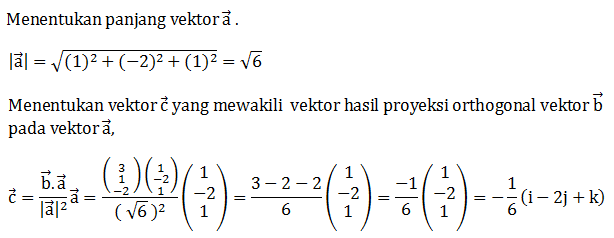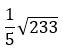Untuk Pembelajaran selanjutnya…
Vektor merupakan besaran yang mempunyai panjang dan arah. Contoh : vektor memiliki titik pangkal P dan titik ujung Q. Sedangkan panjang vektor ![]() dilambangkan dengan
dilambangkan dengan ![]() . Vektor dapat ditulis dengan huruf kecil misalkan
. Vektor dapat ditulis dengan huruf kecil misalkan ![]() ,
, ![]() ,
, ![]() . Misalkan pada gambar dibawah ini:
. Misalkan pada gambar dibawah ini:
Maka vektor ![]() dapat ditulis
dapat ditulis ![]() . Pada diagram cartesius jika dimisalkan titik A (a1, a2) dan titik B (b1, b2)
. Pada diagram cartesius jika dimisalkan titik A (a1, a2) dan titik B (b1, b2)
Secara geometri penjumlahan vektor ![]() dapat dilakukan dengan dua cara yaitu sebagai berikut
dapat dilakukan dengan dua cara yaitu sebagai berikut
Jika tegak lurus antara vektor ![]() dengan vektor
dengan vektor ![]() maka
maka ![]() .
.![]() = 0
= 0
Jika vector (a1, a2, a3) dan vektor (b1, b2, b3) sudut yang dapat dibentuk dari kedua vektor terbut adalah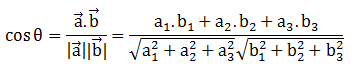
Vektor-vektor u, v, dan w tak nol dan | u | = | v |, Jika | v-w | = | u-w | maka…
PEMBAHASAN :
Diketahui:
| v – w | = | u – w |
Kedua sisi di akarkan![]()
v.v + w.w – 2v.w = u.u + w.w – 2 u.w
|v|2 + |w|2 – 2v.w = |u|2 + |w|2 – 2u.w
Dari soal diketahui | u | = | v | maka
v.w = u.w
u.w – v.w = 0
(u.w).w = 0
Karena perkaliannya = 0 maka (u-v) tegak lurus w
Jawaban : D
Soal No.4 (SBMPTN 2014)
Vektor – vektor u, v, dan x tidak nol. Vektor u + v tegak lurus u –x , jika …
- | u + v | = | u – v |
- | v | = | x |
- u.u = v.v, v = -x
- u.u = v.v , v = x
- u.v = v.v
PEMBAHASAN :
Diketahui
u + v tegak lurus u – x, maka:
(u + v ) . ( u – x ) = 0
u.u –u .x +u.v – v.x = 0
Jika v = x maka
u.u – u.v + u.v – v.v = 0
u.u – v.v = 0
u.u = v.v = 0
Jawaban : D
Soal No.5 (UN 2012)
- -4
- -2
- 2
- 4
Soal No.6 (SBMPTN 2014)
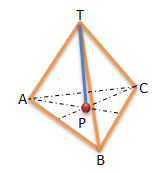
Diberikan limas T.ABC.
 ( u + v + w )
( u + v + w ) ( u + v + w )
( u + v + w ) ( u + v + w )
( u + v + w ) ( u + v + w )
( u + v + w )- u + v + w
Soal No.7 (UN 2005)
Diketahui titik A(6,4,7), B(2,-4,3),dan P(-1,4,2), titik R terletak pada garis AB sehingga AR:RB = 3:1. Panjang vektor PR adalah…
Soal No.8 (SNMPTN 2010)
- 4
- 2
- 1
- -1
Soal No.9 (SBMPTN 2014)
- 1 : 2
- 2 : 1
- 2 : 5
- 5 : 7
- 7 : 5
Soal No.10 (SNMPTN 2012)



- 3
- 5
Soal No.11 (EBTANAS 1989)
Titik R adalah terletak di antara titik P(2,7,8) dan Q(-1,1,-1) yang membagi garis PQ di dalam perbandingan 2:1 maka koordinat R adalah….
- (0,9,6)
- (0,3,2)


- (1,8,7)
Soal No.12 (SIMAK UI 2010)
Soal No.13 (UN 2014)
Soal No.14 (SIMAK UI 2010 IPA)
- -5
- -1
- 1
- 2
- 5
Soal No.15 (UN 2013)
 dan
dan 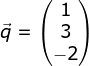 apabila α adalah sudut yang di bentuk antara vektor
apabila α adalah sudut yang di bentuk antara vektor Soal No.16 (SIMAK UI 2010)
- -¼
- -½

- ¼
- ½
Soal No.17 (UN 2011)
- 30o
- 45o
- 60o
- 90o
- 120o
Soal No.18 (UM UGM 2010 IPA)
- 3
- 1
- 1/3
- -1/3
- -1
Soal No.19 (EBTANAS 2001)
Soal No.20 (UMB PTN 2009)
- 60°
- 45°
- 30
- 25
- 20
Soal No.21 (UN 2009)
- 15o
- 30 o
- 45o
- 90o
- 120 o
PEMBAHASAN :
Soal No.22 (SNMPTN 2009)
Soal No.23 (UMPTN 2001)
- ¼
- ½
- 2
- 4
- 8
PEMBAHASAN :
Soal No.24 (UN 2014)
- -3
- -2
- -1
- 1
- 3
Soal No.25 (UMPTN 2004)
- 1
- -1
- 2
- 3
Soal No.26 (UN 2009)
- -3i – 6j – 9k
- i + 2j + 3k
 i +
i +  j + k
j + k- -9i – 18j – 27k
- 3i + 6j +9k
Soal No.27 (SNMPTN 2011)
- -9
- -7
- -5
- 5
- 9
Soal No.28 (UN 2006)
- ½
- 1

- 2

Soal No.29 (SBMPTN 2013)
Soal No.30 (UN 2013)
 (i – 2j + k)
(i – 2j + k) (3i – 2j + 2k)
(3i – 2j + 2k)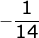 (i – 2j + k)
(i – 2j + k)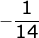 (3i – j + 2k)
(3i – j + 2k) (i – 2j + k)
(i – 2j + k)
Soal No.31 (UN 2004)
- -4 atau -2
- -4 atau 2
- 4 atau -2
- 8 atau -1
- -8 atau 1
Soal No.32
Diketahui titik P (4, 0, -2) dan P(2, 3, -4), tentukan:
- vektor

- panjang vektor

- vektor satuan dari vektor

PEMBAHASAN :

= (2, 3, -4) – (4, 0, -2)
= (-2, 3, -2)
= -2 +3
+3 -2
-2
- panjang vektor

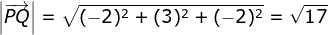
- vektor satuan dari vektor


Soal No.33
- ±

- ±

- ±
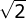
- ±10
- ±5
PEMBAHASAN :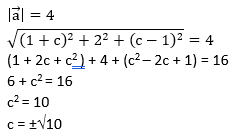
Jawaban : A
Soal No.34
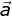 +
+  –
– 
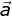 –
–  +
+ 
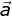 –
–  –
– 
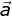 +
+  +
+ 
- –
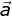 +
+  –
– 
PEMBAHASAN :
ABCD adalah jajar genjang, maka berlaku hubungan:

Jawaban : B
Soal No.35
 + 2
+ 2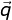 –
– 
- –
 – 2
– 2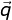 –
– 
 – 2
– 2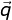 +
+ 
- –
 + 2
+ 2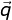 +
+ 
 + 2
+ 2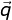 +
+ 
PEMBAHASAN :
Jawaban : E
Soal No.36
- 3
 +
+  – 2
– 2
- 7
 +
+  + 2
+ 2
- 7
 + 13
+ 13 – 3
– 3
 + 3
+ 3 – 2
– 2
- 3
 +
+  + 2
+ 2
PEMBAHASAN :
Jawaban : C
Soal No.37
PEMBAHASAN :
Jawaban : A
Soal No.38
- 5
- 6
- 2
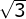
- 4
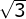
- 3

PEMBAHASAN :
Jawaban : D
Soal No.39

 –
– 
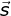

 +
+ 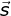
- –

 –
–
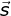

 –
– 
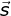

 +
+ 
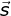
PEMBAHASAN :

Jawaban : A
Soal No.40

 –
– 
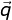

 +
+ 
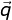
- –

 +
+ 
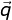
- –

 –
– 
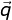

 +
+ 
PEMBAHASAN :
Jawaban : B
Soal No.41
- (1, -2, 15)
- (-3, -2, 1)
- (2, 5, 12)
- (3, -2, 10)
- (3, -5, 10)
PEMBAHASAN :
Jawaban : E
Soal No.42
PEMBAHASAN :
Jawaban : D
Soal No.42
- 6
- 3
- -5
- 1
- -7
PEMBAHASAN :
Syarat vektor segaris yaitu ![]() = k
= k![]()

Perhatikan persamaan (3) dapat diketahui bahwa k = ½
Dengan k = ½
Persamaan (1) → y = 4
Persamaan (2) → x = 2
Maka x + y = 2 + 4 = 6
Jawaban : A
Soal No.43
- 5
- 3
- -2
- 6
- -9
PEMBAHASAN :
Perhatikan persamaan berikut:
Persamaan (1) → – 5 = 2k – 3m → – 5 = 2k – 3m
Persamaan (2) kalikan (- 3) → 12 = – 9k – (- (-3)) → 12 = – 9k + 3m
. 7 = -7k
. k = – 1
-5 = 2k – 3m
-5 = 2(-1) – 3m
-5 = -2 – 3m
3m = -2 + 5
3m = 3
m = 1
maka k – m = – 1 – 1 = – 2
Jawaban : C
Soal No.44
- 5
- 3
- -2
- 6
- -9
PEMBAHASAN :
Perhatikan persamaan berikut:
Persamaan (1) → – 5 = 2k – 3m → – 5 = 2k – 3m
Persamaan (2) kalikan (- 3) → 12 = – 9k – (- (-3)) → 12 = – 9k + 3m
. 7 = -7k
. k = – 1
-5 = 2k – 3m
-5 = 2(-1) – 3m
-5 = -2 – 3m
3m = -2 + 5
3m = 3
m = 1
maka k – m = – 1 – 1 = – 2
Jawaban : C
Soal No.45
PEMBAHASAN :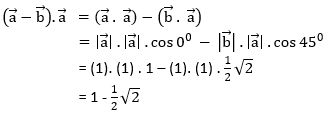
Jawaban : B
Soal No.46
- 9 atau -1½
- 3 atau -½
- 1 atau ½
- 9 atau -½
- 3 atau 1
PEMBAHASAN :
Jawaban : A
Soal No.47
PEMBAHASAN :
Jawaban : C
Soal No.48
PEMBAHASAN :
Jawaban : E
Soal No.49
PEMBAHASAN :
Jawaban : D
Soal No.50
- 1 dan 2
- 2 dan -3
- -2 dan -3
- 4 dan -1
- -1 dan -3
PEMBAHASAN :
Diketahui:![]() = (6a, 1, a3)
= (6a, 1, a3)![]() = (1, 5a2 , 1)
= (1, 5a2 , 1)![]() .
.![]() = (6a)(1) + (1)(5a2 ) + (a3 )(1)
= (6a)(1) + (1)(5a2 ) + (a3 )(1)
F (a) = 6a + 5a2 + a3
Syarat stasioner, sebagai berikut:
F(a) = 0
6a + 5a2 + a3 = 0 (dibagi a)
6 + 5a + a2 = 0
(a + 3)(a + 2) = 0
Jawaban : C
Soal No.51
Jika diketahui titik-titik sudut suatu segitiga ABC adalah A = (3, 8, 2), B = (4, 1, -2), dan C = (-1, 3, 5). Luas dari segitiga ABC tersebut adalah….
- 12,2
- 16,2
- 27,1
- 34,2
- 54,3
PEMBAHASAN :
Jika dimisalkan
Vektor ![]() =
= ![]()
. = (4, 1, -2) – (3, 8, 2) = (1, -7, -4)
Vektor ![]() =
= ![]()
. = (-1, 3, 5) – (3, 8, 2) = (-4, -5, 3)
. = ((-7).3 – (-5).(-4))![]() + ((-4).(-4) – 3.1)
+ ((-4).(-4) – 3.1)![]() + (1.-5 – (-7).(-4))
+ (1.-5 – (-7).(-4))![]()
. =(-21 – 20)![]() + (16 – 3)
+ (16 – 3)![]() + (-5 – 28)
+ (-5 – 28)![]()
. =(-41)![]() + 13
+ 13![]() -33
-33![]()
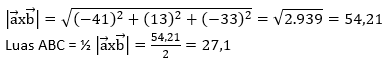
Jawaban : C
Soal No.52
- 4
 + 2
+ 2 + 3
+ 3
- -4
 –
–  + 3
+ 3
- 6
 + 3
+ 3 + 2
+ 2
 + 4
+ 4 – 6
– 6
- 6
 + 4
+ 4 + 4
+ 4
PEMBAHASAN :
Jawaban : E
Soal No.53
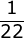 (1, 1, 1)
(1, 1, 1)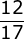 (1, 3, 5)
(1, 3, 5) (3, 1, 1)
(3, 1, 1) (3, 1, 2)
(3, 1, 2) (1, 1, 3)
(1, 1, 3)
PEMBAHASAN :
Perhatikan gambar kubus OABCDEFG!
Gambar
Jawaban : B
Soal No.54
PEMBAHASAN :
Jawaban : E
Soal No.55
- -1
- -2
- -3
- -4
- -5
PEMBAHASAN :
Jawaban : D
Semoga Bermanfaat