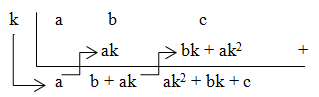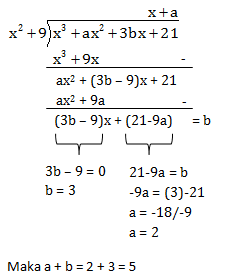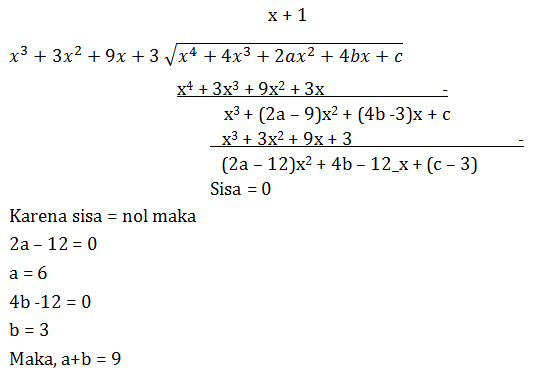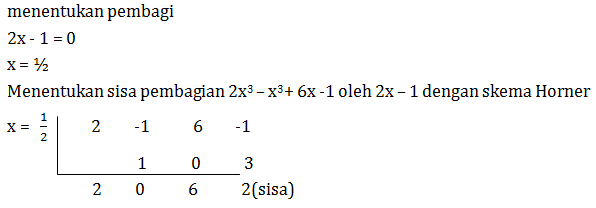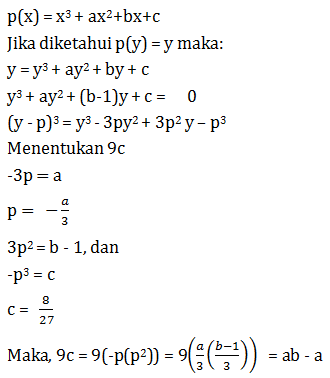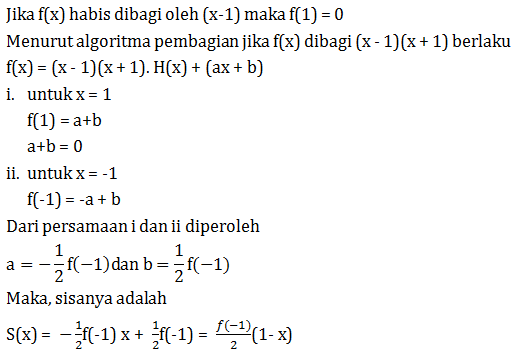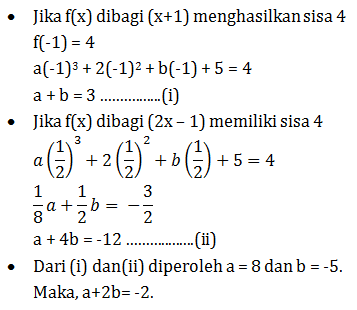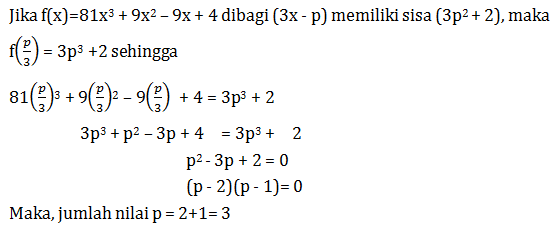Rangkuman, Contoh Soal & Pembahasan Suku Banyak

Pengertian

Merupakan suatu bentuk yang memuat variabel berpangkat. Dinyatakan sebagai berikut:

a_nxⁿ + a_n-1xⁿ + a_n-2x^n-2 + ….+a₂x² +a₁x + a_o
Dengan syarat:
n merupakan bilangan cacah
a_n ≠ 0
a_n, a_n-1, .., a₂,a₁, a_o­ merupakan bilangan real yang disebut koefisien suku banyak

xⁿ, x^n-1, …., x², x disebut variabel atau peubah

NILAI SUKU BANYAK

Untuk menentukan nilai suku banyak dapat dilakukan dengan dua cara, yaitu

Cara Substitusi

Jika suku banyak f(X) = ax³ + bx² + cx + d. Jika nilai x diganti k maka nilai suku banyak f(x) = ak³ + bk² + ck + d

Contoh soal :
Hitunglah nilai suku banyak berikut ini untuk nilai x yang diberikan
f(x) = 2x³ + 4x² – 18 untuk x = 3
Jawaban:
f(x) = 2x³ + 4x² – 18
f(3) = 2.3³ + 4. 3² – 18
f(3) = 2 . 27 + 4.9 – 18
f(3) = 54 + 36 – 18
f(3) = 72
Maka nilai suku banyak f(x) untuk x = 3 adalah 72

LIHAT JUGA : Video Pembelajaran Suku Banyak

Cara Horner/bangun/skema/Sintetik

Jika akan menentukan nilai suku banyak f(x) = ax² + bx + c untuk x = k dengan cara Horner maka dapat disajikan dengan bentuk skema berikut.

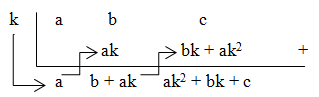
Contoh soal:
Hitunglah nilai suku banyak untuk nilai x yang diberikan berikut ini
f(x) = x³ + 2x² + 3x – 4 untuk x = 5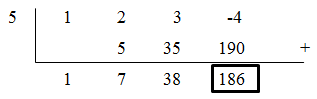

Jadi nilai suku banyak f(x) untuk x = 5 adalah 186

Derajat Suku Banyak dan Hasil Bagi dan Sisa Pembagian

Derajat merupakan pangkat tertinggi dari variabel yang terdapat pada suku banyak. Contoh ax³ + bx² + cx + d memiliki derajat n = 3

Jika suku banyak f(x) berderajat n dibagi oleh fungsi berderajat satu maka akan menghasilkan hasil bagi berderajat (n-1) dan sisa pembagian berbentuk konstanta

Contoh soal:
Tentukan derajat dan hasil bagi dan sisa pembagian suku banyak berikut.
2x³ + 4x² – 18 dibagi x – 3

Cara Horner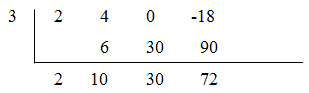

Diperoleh 2x² + 10x + 30 sebagai hasil bagi berderajat 2 dan 72 sebagai sisa pembagian

Menentukan hasil bagi dan sisa pembagian suku banyak oleh bentuk linear atau kuadrat

1. Suku banyak f(x) dibagi (ax + b) menghasilkan sebagai hasil bagi dan sebagai sisa pembagian, sedemikian hingga f(x) = (ax + b) +
   Contoh Soal:
   Tentukanlah hasil bagi dan sisanya jika memakai cara horner
   f(x) = 2x³ + x² + x + 10 dibagi (2x + 3)
   Jawaban: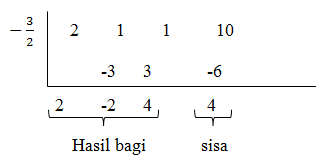
   
   Karena pembaginya
   2x + 3 =
   Faktor pengalinya =
   Hasil baginya = = x² – x + 2
   Maka sisa pembagian = 4
2. Suku banyak f(x) dibagi ax² + bx + c dapat difaktorkan menjadi
   (ax – p₁)(x – p₂) dapat ditulis f(x) = (ax² + bx + c) . h₂(x) + (ax – p₁).h₁(p₂) + f
   di mana h₂(x) merupakan hasil bagi dan (ax – p₁) h₁(p₂) + f merupakan sisa pembagian.
   Contoh soal:
   Tentukanlah hasil bagi dan sisa pembagian jika 2x³⁺ + x² + 5x – 1 dibagi (x² – 1)
   Jawab:
   (x² – 1) dapat difaktorkan menjadi (x+1)(x-1)
   Cara Horner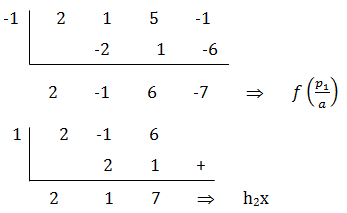
   
   Jadi (2x + 1) merupakan hasil bagi dan 7x merupakan sisa pembagian

Teorema sisa

1. Jika suku banyak f(x) dibagi (x – k), maka sisa pembaginya adalah f(k).
2. Jika suku banyak f(x) dibagi (ax + b), maka sisa pembaginya adalah .
3. Jika suku banyak f(x) dibagi (x – a)(x – b), maka sisanya adalah px + q dimana f(a) = pa + q dan f(b) = pb + q.

Teorema faktor

1. Jika f(x) suatu suku banyak, maka (x – a) faktor dari f(x) jika dan hanya jika a akar persamaan f(a) = 0.
2. (ax-b) adalah faktor dari suku banyak f(x), jika dan hanya jika f = 0
3. Suku banyak f(x) habis dibagi (x-a) jika dan hanya jika f(a) = 0

Akar-akar rasional persamaan suku banyak

1. Suku banyak berderajat dua: ax²+ bx + c = 0
   1. x₁ + x₂ =
   2. x₁ ⋅ x₂ =
2. Suku banyak berderajat tiga: ax³ + bx² + cx + d = 0
   1. x₁ + x₂ + x₃ =
   2. x₁ ⋅ x₂ + x₂ ⋅ x₃ + x₁ ⋅ x₃ =
   3. x₁ ⋅ x₂ ⋅ x₃ =
3. Suku banyak berderajat empat: ax⁴ + bx³ + cx² + dx + e = 0
   1. x₁ + x₂ + x₃ + x₄ =
   2. x₁ ⋅ x₂ ⋅ x₃ + x₂ ⋅ x₃ ⋅ x₄ + x₃ ⋅ x₄ ⋅ x₁ + x₄ ⋅ x₁ ⋅ x₂ =
   3. x₁ ⋅ x₂ + x₁ ⋅ x₃ + x₁ ⋅ x₄ + x₂ ⋅ x₃ + x₂ ⋅ x₄ + x₃ ⋅ x₄ =
   4. x­₁ ⋅ x₂ ⋅ x₃ ⋅ x₄ =

Soal No.1 (UTBK 2019)

Jumlah semua ordinat penyelesaian sistem persamaan

adalah…

1. -2
3. 1
4. 2
5. 4

PEMBAHASAN :

Jawaban A

Soal No.2 (UTBK 2019)

Jika p(x) = ax³ + bx² + 2x – 3 habis dibagi x² + 1, maka nilai 3a – b adalah…

PEMBAHASAN :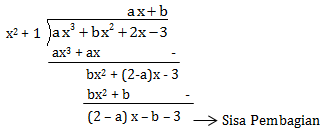

Karena habis dibagi, berarti sisa pembagiannya nol:
(2 – a)x – b – 3 = 0
⇒ 2 – a = 0 dan -b – 3 = 0
⇒ a = 2 dan b = -3
∴ 3a – b = 3.(2) – (-3) = 6+3 = 9
Jawaban D

Soal No.4 (SBMPTN 2013 IPA)

suku banyak x³ + 3x² + 9x + 3 membagi habis x⁴ + 4x³ + 2ax² + 4bx + c. Nilai a + b adalah…

1. 12
2. 10
3. 9
4. 6
5. 3

PEMBAHASAN :

Jawaban : C

Soal No.5 (UN 2014)

Suku banyak berderajat 3, jika dibagi (x² + 2x – 3) bersisa (3x – 4), jika dibagi (x² – x -2) bersisa (2x + 3). Suku banyak tersebut adalah …

1. x³ – x² – 2x – 1
2. x³ + x ² – 2x – 1
3. x ³ + x² + 2x – 1
4. x³ + 2x² – x – 1
5. x³ + 2x² + x + 1

PEMBAHASAN :
Sesuai algoritma pembagian dan teorema sisa:

1. Jika f(x) dibagi (x² + 2x – 3) bersisa (3x – 4), sehingga:
   f (x)= (x² + 2x – 3)(ax + b) + (3x – 4) = (x – 1)(x + 3)(ax + b) + (3x – 4)
   f (1) = 3(1) – 4 = -1
   f(-3) = 3(-3) – 4 = -13
2. Jika f(x) dibagi (x² – x – 2) bersisa (2x + 3), sehingga:
   f(x) = (x² – x – 2)(ax + b) + (2x + 3) = (x – 2)(x + 1)(ax + b) + (2x + 3)
   f(1) = -1
   (-1)(2)(a + b)+(2+3) = -1
   -2a – 2b = -6
   a + b = 3 …(1)
   f(-3)= -13
   (-5)(-2)(-3a + b)+(2(-3)+ 3) = -13
   -30a + 10b = -10
   -3a + b = -1…(2)

Persamaan (1) dan (2) dieliminasi, sehingga diperoleh a = 1 dan b = 2.
Sehingga:
f (x)= (x² – x – 2)(ax + b) + (2x + 3) = (x² – x – 2)(x + 2) + (2x + 3)
f (x)= x³ + x² – 2x – 1
Jawaban : B

Soal No.6 (SIMAK UI 2010 IPA)

Diketahui 2x² + 3px – 2q dan x² + q mempunyai faktor yang sama, yaitu x – a, dimana p, q dan a merupakan konstanta bukan nol. Nilai 9p² + 16q adalah …

1. -2
2. -1
4. 1
5. 2

PEMBAHASAN :

Jawaban : C

Soal No.7 (UN 2013)

Salah satu faktor dari suku banyak f(x)= 2x³ + ax² -11x + 6 yaitu (x + 2). Faktor linier yang lain adalah …

1. 2x + 1
2. 2x + 3
3. x – 3
4. x – 2
5. x – 1

PEMBAHASAN :

Jawaban : C

Soal No.8 (SBMPTN 2014)

Diketahui P dan Q suatu polinomial sehingga P(x) Q(x) dibagi x² – 1 bersisa 3x + 5. Jika Q(x) dibagi x – 1 bersisa 4, maka P(x) dibagi x – 1 bersisa….

1. 8
2. 6
3. 4
4. 2
5. 1

PEMBAHASAN :

• Jika Q(x) dibagi (x – 1) menghasilkan sisa 4
  Q(1) = 4

• P(x)Q(x) dibagi x² – 1 = (x – 1)(x + 1) menghasilkan sisa (3x + 5)
  • x = 1
    P(1)Q(1) = 3(1) + 5 = 8
    P(1)(4) = 8
    P(1) = 2
  • x = -1
    P(-1)Q(-1) = 3(-1) + 5 = 2

• Jika P(x) dibagi (x – 1) akan menghasilkan sisa = P(1) = 2

Jawaban : A

Soal No.9 (UN 2011)

Diketahui (x – 2) dan (x – 1) adalah faktor-faktor suku banyak P(x) = x³ + ax² – 13x + b. Jika akar-akar persamaaan suku banyak tersebut adalah x_1, x_2, dan x₃, untuk x₁ > x₂ > x₃, maka nilai x₁ – x₂ – x₃ = …

1. 8
2. 6
3. 3
4. 2
5. -4

PEMBAHASAN :

Jawaban : B

Soal No.10 (UMPTN 2006)

Diketahui p(x) = (x – 1)(x² – x – 2) q(x) + ax + b dengan q(x) suatu suku banyak. Jika p(x) dibagi dengan (x + 1) bersisa 10 dan jika dibagi dengan (x – 1) bersisa 20 maka jika p(x) dibagi dengan (x – 2) bersisa….

1. 10
3. 5
4. 15
5. 25

PEMBAHASAN :
Diketahui p(x) = (x – 1)(x² – x – 2)q(x) + (ax + b) = ( x – 1)(x + 1)(x – 2).q(x) + (ax + b).

• Jika p(x) dibagi (x + 1) menghasilkan sisa 10
  p(-1) = 10
  -a + b = 10 …. (1)

• Jika p(x) dibagi (x – 1) menghasilkan sisa 20
  p(1) = 20
  a + b = 20 …. (2)

Dari persamaan 1 dan 2 diperoleh a = 5 dan b = 15

• Maka jika p(x) dibagi (x – 2) menghasilkan (ax + b)
  p(2) = 2a + b = 2(5) + (15) = 25

Jawaban : E

Soal No.11 (UN 2010)

Suku banyak x³ + 2x² – px + q, jika dibagi (2x – 4) bersisa 16 dan jika dibagi (x + 2) bersisa 20. Nilai dari 2p + q = …

PEMBAHASAN :
Diketahui f(x) = x³ + 2x² – px + q.
Sesuaikan teorema sisa maka

1. f(2) = 16
   (2)³ + 2(2)² – p(2) + q = 16
   -2p + q = 0
2. f(-2) = 20
   (-2)³ + 2 (-2)² – p(-2) + q = 20
   2p + q = 20

Dari persamaan i dan ii diperoleh nilai dari 2p + q = 20
Jawaban : D

Soal No.12 (UM UGM 2013)

Suku banyak P(x) dibagi x² – x – 2 mempunyai hasil bagi Q(x) dan sisa x + 2. Jika Q(x) dibagi x + 2 mempunyai sisa 3, maka sisa P(X) dibagi x² +3x + 2 adalah….

1. -11x – 10
2. -10x – 11
3. 11x – 10
4. 10x + 11
5. 11x + 10

PEMBAHASAN :

• Jika Q(x) dibagi x + 2 menghasilkan sisa 3
• Jika P(x) dibagi x² – x – 2 = (x – 2)(x + 1) mempunyai hasil bagi Q(x) dan sisa x + 2 sehingga
  P(x) = (x – 2)(x + 1)Q(x) +(x + 2)
  P(x) = (x – 2)(x + 1){(x + 2).H(x) + (3)} + (x + 2)
  untuk x = -1
  P(-1) = (-1) + 2 = 1
  untuk x = -2
  P(-2) = (-2 – 2)(-2 + 1)(0 + 3) + (-2 + 2) = 12
• Jika P(x) dibagi x² + 3x + 2 = (x + 2)(x + 1) menghasilkan sisa (ax + b)
  P(x) = (x + 2)(x + 1). Q(x) + (ax + b)
  P(-1) = -a + b
  -a + b = -1 …..(1)
  P(-2) = -2a + b
  -2a + b = 12 …..(2)

Dari persamaan (1) dan (2) diperoleh a = -11 dan b = -10
Maka sisanya adalah -11x – 10
Jawaban : A

Soal No.13 (UN 2004)

Suku banyak (x⁴ – 3x³ – 5x² + x – 6) dibagi oleh (x² – x – 2) sisanya sama dengan …

1. 16x + 8
2. 16x – 8
3. -8x + 16
4. -8x – 16
5. -18x – 24

PEMBAHASAN :
Diketahui P(x) = (x² – x – 2)(x + 1) pembagi suku banyak f(x) = (x⁴ – 3x³ – 5x² + x – 6)
Karena pembagiannya berderajat 2 maka sisanya berderajat 1 yaitu S(x) = mx + n
Sisa dapat diperoleh dengan algoritma pembagian
f(x) = (x – 2)(x + 1). H(x) + (mx + n)

1. Untuk x = 2
   (2)⁴ – 3(2)³ – 5(2)² + (2) – 6 = 2m + n
   2m + n = -32
2. Untuk x = -1
   (-1)⁴ – 3(-1)³ – 5(-1)² + (-1) – 6 = -m + n
   -m + n =-8

Persamaan i dan ii dieliminasi diperoleh
m = -8 dan n = -16
Maka, sisanya adalah -8x – 16.
Jawaban : D

Soal No.14 (SNMPTN 2011 IPA)

Kedua akar suku banyak S(x) = x²– 63x + c merupakan bilangan prima. Banyak nilai c yang mungkin adalah…

2. 1
3. 2
4. 3
5. lebih dari 3

PEMBAHASAN :
S(x) = x² – 63x = c memiliki akar x₁ dan x_1, maka x₁ + x₂ =  = 63 dan x_1.x₂ = = c
Dari penjumlahan dua akar diatas diketahui bernilai ganjil (63) maka satu bilangan merupakan ganjil dan satu bilangan mrupakan bilangan genap.
Diketahui kedua akar merupakan bilangan prima maka bilangan genap yang merupakan bilangan prima adalah 2 (x₁ = 2) sedangkan bilangan ganjil nya dapat dihitung dengan penjumlahan kedua akarnya tadi. x₁+x₂ = 63 sehingga diperoleh x₂ = 61. Maka, banyaknya nilai c yang mungkin ada 1, yaitu (2 x 61 = 122)
Jawaban : C

Soal No.15 (EBTANAS 1991)

Suku banyak f(x) dibagi oleh (x² – 2) memberikan sisa (3x + 1) sedangkan dibagi oleh (x² + x) sisanya (1 – x). Sisa pembagian f(x) oleh (x² – 1) adalah …

1. (x + 3)
2. (3 – x)
3. (x – 3)
4. (3x + 1)
5. 2

PEMBAHASAN :
Menurut teorema sisa

1. Jika f(x) dibagi (x² – 2) = x(x – 1) memiliki sisa (3x – 1)
   1. f(0) = 3(0) + 1 = 1
   2. f(3) = 3(3) + 1 = 10
2. Jika f(x) dibagi (x² + 2) = x(x+1) memiliki sisa (1- x)
   1. f(0) = 1 – (0) = 1
   2. f(1) = 1 – (-1) = 2

Sisa pembagian f(x) oleh (x² – 1) = (x – 1) (x + 1) dapat diperoleh dengan algoritma pembagian
f(x) = (x – 1)(x + 1).H(x) + S(x)
f(x) = (x – 1)(x + 1).H(x) + (mx + n)

1. Untuk x = 1
   f(1) = m + n → m + n = 4
2. Untuk x = -1
   f(-1) = -m + n → -m + n = 2

Dari hasil i dan ii diperoleh m = 1 dan n = 3.
Dan sisanya adalah x + 3 .
Jawaban : A

Soal No.16 (SIMAK UI 2012 IPA)

Sisa dari pembagian (3x – 10)¹⁰ + (-4x + 13)¹³ + (5x – 16)¹⁶ + (ax + b)¹⁹ oleh x -3. Nilai a dan b yang mungkin adalah …

1. a = 1, b = -3
2. a = 0, b= 0
3. a = -1, b = 3
4. a = -6, b = 19

PEMBAHASAN :
Jika f(x) = ( 3x – 10) ¹⁰ + (-4x + 13)¹³ + (5x – 16)¹⁶ + (ax + b)¹⁹. dibagi (x – 3) menghasilkan sisa 3 maka f(3) = 3 sehingga
(3(3)-10)¹⁰– (-4(3) + 13)¹³ + (5(3)-16)¹⁶ + (a(3)+b)¹⁹ = 3
1 + 1 + 1 + (3a + b)¹⁹ = 3
(3a + b)¹⁹ = 0
3a + b = 0

1. a = 1, b = -3 (benar)
   3(1) + (-3) = 0
2. a = 0, b = 0 (benar)
   3(0) + (0) = 0
3. a = -1, b = 3 (benar)
   3(-1) + (3) = 0
4. a = -6, b = 19 (salah)
   3(-6) + 19 ≠ 0

Jawaban benar 1, 2, 3
Jawaban : A

Soal No.17 (EBTANAS 2002)

Suku banyak (2x³ + ax² – bx + 3) dibagi (x² – 4) bersisa (x + 23). Nilai a + b =…

1. -1
2. -2
3. 2
4. 9
5. 12

PEMBAHASAN :
Diketahui f(x) = (2x³ + ax² – bx + 3).
Jika f(x) dibagi (x²-4) = (x-2)(x+2) akan memiliki sisa (x + 23), maka

1. f(2) = (2) + 23
   2(2)³ + a(2)² – b(2) + 3 = 25
   2a – b = 3
2. f(-2) = (-2) + 23
   2(-2)³ + a(-2)² – b(-2) + 3 = 21
   2a + b = 17.

Dari i dan ii diperoleh a = 5 dan b = 7. Maka a + b = 12.
Jawaban : E

Soal No.18 (UMPTN 2005)

Jika f(x) = ax³ + 3bx² + (2a – b ) x + 4 di bagi dengan (x – 1) sisanya 10_, sedangkan jika di bagi dengan (x+2) sisanya 2, nilai a dan b berturut-turut adalah…

1.  dan 1
2.  dan 1
3. 1 dan
4. 1 dan
5.  dan 1

PEMBAHASAN :
Diketahui
f(x) = ax³ + 3bx² + (2a-b) x + 4

• Jika f(x) dibagi (x-1) memiliki sisa 10
  f(1) = 10
  a(1)³ + 3b(1)² + (2a – b)(1) + 4 = 10
  3a + 2b = 6 … (i)
• Jika f(x) dibagi (x + 2 ) sisa 2
  f(-2) = 2
  a(-2)³ + 2b(-2)² + (2a – b)(-2) + 4 = 2
  -12a + 14b = -2
  6a – 7b = 1 … (ii)

Dari persamaan (i) dan (ii) di peroleh
a = dan b = 1
Jawaban : A

Soal No.19 (UN 2005)

Suku banyak P(x)= x³ – 2x + 3 dibagi oleh x² – 2x – 3, sisanya adalah …

1. 
2. 9x – 5
3. 5x + 3
4. 11x – 9
5. 5x + 9

PEMBAHASAN :

Jawaban : E

Soal No.20 (SNMPTN 2012 IPA)

Jika suku banyak 2x³ – x² + 6x – 1 dibagi 2x – 1 maka sisanya adalah…

1. -10
2. -1
3. 1
4. 2
5. 23

PEMBAHASAN :

Jawaban : D

Soal No.21 (UN 2007)

Sisa pembagian suku banyak f(x) oleh (x+2) adalah 4, jika suku banyak tersebut dibagi (2x – 1) sisanya 6. Sisa pembagian suku banyak tersebut oleh 2x² + 3x – 2 adalah …

1. 
2. 
3. 4x + 12
4. 4x + 4
5. 4x – 4

PEMBAHASAN :

Jawaban : A

Soal No.22 (SIMAK UI 2012 IPA)

Misalkan f(x) = (x – 3)³ + (x – 2)² + (x – 1). Maka sisa dari pembagian f(x + 2) oleh x² – 1 adalah …

1. -2 + 5x
2. -9 + 14x
3. 5 – 2x
4. 14 – 9x
5. 11 + 19x

PEMBAHASAN :
f(x) = (x – 3)³ + (x – 2)² + (x – 1)
f(x + 2) = ((x+2) – 3)³ + ((x + 2) – 2)² + ((x +2) – 1) =( x – 3)³ + x² + (x + 1)
Jika f(x + 2) dibagi x² – 1 = (x – 1)(x + 1) berlaku
f(x + 2) = (x – 1)(x + 1). H(x) + (ax + b)

• Untuk x = 1
  f(3) = a + b
  a + b = (1 – 1)³ + 1² +(1 + 1)
  a + b = 3…(i)
• Untuk x = – 1
  f(1) = -a + b
  -a + b = (- 1 – 1)³ + (-1)² + (-1 + 1)
  – a + b = -7 …… (ii)

Dari persamaan (i) dan (ii) akan diperoleh a = 5 dan b = -2 .
Maka, sisanya adalah 5x – 2.
Jawaban : A

Soal No.23 (UN 2008)

Salah satu faktor suku banyak P(x) = x⁴ – 15x² – 10x + n adalah (x + 2) faktor lainnya adalah….

1. x – 4
2. x + 4
3. x + 6
4. x – 6
5. x – 8

PEMBAHASAN :

Jawaban : C

Soal No.24 (SNMPTN 2008 IPA)

Diketahui suku banyak p(x) = x³ + ax² + bx + c dengan a, b, dan c konstan. Jika terdapat tepat satu nilai y yang memenuhi p(y) = y, maka 9c =…

1. ab
2. a + b
3. ab – a
4. a – b
5. ab + 2

PEMBAHASAN :

Jawaban : C

Soal No.25 (UN 2009)

Suku banyak f(x) jika dibagi (x – 1) bersisa 4 dan bila dibagi (x + 3) bersisa -5. Suku banyak g(x) jika dibagi (x – 1) bersisa 2 dan bila dibagi (x + 3) bersisa 4, jika h(x) = f(x).g(x) maka sisa pembagian h(x) oleh (x² + 2x – 3) adalah….

1. 6x + 2
2. x + 7
3. 7x + 1
4. -7x + 15
5. 15x – 7

PEMBAHASAN :

• Jika f(x) dibagi (x – 1) memiliki sisa 4
  f(1) = 4
  Jika f(x) dibagi (x + 3) memiliki sisa-5
  f(-3) = -5
• Jika g(x) dibagi (x – 1) memiliki sisa 2
  g(1) = 2
  Jika g(x) dibagi (x + 3) memiliki sisa 4
  g(-3) = 4
• h(x) = f(x). g(x)
  • untuk x = 1
    h(1) = f(1). g(1) = 8
  • untuk x = -3
    h(-3) = f(-3).g(-3) = -20
• Sisa pembagian h(x) oleh (x² + 2x – 3) = (x + 3)(x – 1) dapat diperoleh dengan algoritma pembagian
  h(x) = (x + 3)(x – 1).H(x) + S(x)
  h(x) = (x + 3)(x – 1).H(x) + (mx + n)
  1. untuk x = -3
     h(-3) = -3m + n
     -3m + n = -20
  2. untuk x = 1
     h(1) = m + n
     m + n = 8

Dari i dan ii diperoleh m = 7 dan n = 1. Maka sisanya adalah 7x + 1
Jawaban : C

Soal No.26 (SIMAK UI 2009 IPA)

Jika suku banyak f(x) habis dibagi oleh (x – 1) maka sisa pembagian f(x) oleh (x – 1)(x + 1) adalah …

PEMBAHASAN :

Jawaban : D

Soal No.27 (UN 2010)

Diketahui (x – 2) adalah faktor suku banyak f(x) = 2x³ + ax² + bx – 2. Jika f(x) dibagi (x + 3) maka sisa pembagiannya adalah -50. Nilai (a + b) = …

1. 10
2. 4
3. -6
4. -11
5. -13

PEMBAHASAN :

• Jika (x – 2) adalah faktor dari f(x) = 2x³ + a + bx – 2 maka berlaku f(2) = 0
  2 + a + b(2) – 2 = 0
  2a + b = -7 …………………(i)
• f(x) dibagi (x+3) memiliki sisa -50
  f(-3) = -50
  2(-3)³ + a(-3)² + b(-3) – 2 = -50
  3a – b = 2…………….(ii)
• Dari (i) dan (ii) diperoleh a = -1 dan b = -5. Maka, a + b = -6.

Jawaban : C

Soal No.28 (SIMAK UI 2010 IPA)

Diketahui P (x) = ax⁵ + bx – 1, dengan a dan b konstan. Jika P(x) dibagi dengan (x-2010) bersisa 6. Jika P (x) dibagi dengan (x +2010) akan bersisa …

1. -8
2. -2
3. -1
4. 1
5. 8

PEMBAHASAN :

• Jika P(x) dibagi (x – 2010) memiliki sisa 6
  P(2010) = 6
  a (2010)⁵ + b(2010) – 1 = 6
  (2010)⁵ a + 2010b-7 = 0…(i)
• Jika P(x) dibagi (x + 2010) memiliki sisa S(x)
  P(-2010) = S(x)
  a(-2010)⁵ + b(-2010) – 1= S(x)
  (-2010)⁵ a – 2010b – 1 = S(x)………………………..(ii)
• Dari persamaan (i) dan (ii) diperoleh S(x) = -8

Jawaban : A

Soal No.29 (UN 2011)

Diketahui suku banyak f(x) = ax³ + 2x² + bx + 5, a ≠ 0 dibagi oleh (x +1) sisanya 4 dan di bagi oleh (2x – 1) sisanya juga 4.Nilai dari a + 2b adalah…..

1. -8
2. -2
3. 2
4. 3
5. 8

PEMBAHASAN :

Jawaban : B

Soal No.30 (SIMAK UI 2010 IPA)

Pada pembagian suku banyak 81x³ + 9x² + 4 dengan (3x – p) diperoleh sisa (3p³ + 2). Jumlah nilai-nilai p yang memenuhi adalah …

PEMBAHASAN :

Jawaban : B

Soal No.31 (UN 2012)

Suatu suku banyak berderajat 3 jika dibagi x² – 3x + 2 bersisa 4x – 6 dan jika dibagi x² – x – 6 bersisa 8x – 10.Suku banyak tersebut adalah…….

1. x³ – 2x² + 3x – 4
2. x³ – 3x² + 2x – 4
3. x³ + 2x² – 3x – 7
4. 2x³ + 2x² – 8x + 7
5. 2x³ + 4x² – 10x + 9

PEMBAHASAN :
Misal f(x) adalah suku banyak berderajat 3.
Berdasarkan algoritma pembagian dan teorama sisa

1. Jika f(x) dibagi (x² – 3x + 2) memiliki sisa (4x – 6),maka
   f(x) = (x² -3x + 2)(ax + b) + (4x – 6) = (x – 1)(x – 2)(ax + b) + (4x – 6)
   f(1) = 4(1) – 6 = -2
   f(2) = 4(2) – 6 = 2
2. Jika f(x) dibagi (x² – x – 6) memiliki sisa (8x – 10) maka
   f(x) = (x² – x – 6)(ax + b) + (8x – 10) = (x – 3)(x + 2)(ax + b) + (8x – 10)
   • f(1) = -2
     (-2)(3)(a + b) + (8 – 10) = -2
     a + b = 0…….(1)
   • f(2) = 2(-1)(4)(2a + b) + (8(2)-10) = 2
     2a + b=1……(2)

Persamaan (1) dan (2) dieliminasi,diperoleh a = 1 dan b = -1.
Maka, suku banyak tersebut adalah
f(x) = (x² – x – 6)(ax + b) + (8x – 10) = (x² – x – 6)(x – 1) + (8x – 10)
f(x) = x³ – x² – x² + x – 6x + 6 + 8x – 10
f(x) = x³ – 2x² + 3x – 4
Jawaban : A

Soal No.32 (SBMPTN 2014 IPA)

Diketahui P(x) suatu polinomial. Jika P(x + 1) dan P(x – 1)masing-masing memberikan sisa 2 apabila masing-masing di bagi x – 1, maka P(x) di bagi x²-2x memberikan sisa….

1. x + 2
2. 2x
3. x
4. 1
5. 2

PEMBAHASAN :

• Jika P(x-1) di bagi (x – 1) menghasilkan sisa 2
  P(1+1) = 2
  P(2) = 2
• Jika P(x – 1) di bagi (x -1) menghasilkan sisa 2
  P(1- 1) = 2
  P(0) = 2
• P(x) dibagi (x² – 2x) = x(x – 2) sisa (ax + b)
  P(0) = b
  b = 2
  P(2) = 2a + b
  2a + 2 = 2
  a = 0
  Maka,sisanya 2.

Jawaban : E

Soal No.33 (UN 2013)

Salah satu faktor dari suku banyak P(x) = 2x³ – 5x² + px + 3 adalah (x+ 1). Faktor linier lainnya dari suku banyak tersebut adalah……

1. x – 1
2. x – 2
3. x + 2
4. 2x – 1
5. 2x + 1

PEMBAHASAN :

Jawaban : D