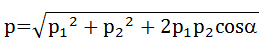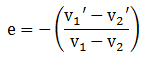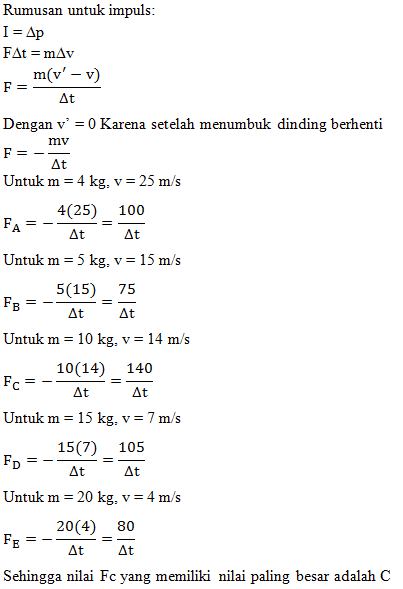Rangkuman, Contoh Soal & Pembahasan Momentum & Impuls

Momentum

Momentum merupakan besaran vektor yang mempunyai arah sama dengan arah kecepatan benda. Momentum adalah hasil kali antara massa benda dengan kecepatan gerak benda tersebut. Sehingga momentum dapat dirumuskan sebagai berikut:

p = m.v

Keterangan:
p          = momentum (kg.m/s)
m         = massa benda (kg)
v          = kecepatan benda (m/s)

Semakin besar massa benda, semakin besar momentumnya. Demikian pula jika semakin cepat benda bergerak, semakin besar pula momentumnya.

Momentum merupakan besaran vektor yang searah dengan kecepatan benda. Penjumlahannya mengikuti aturan penjumlahan vektor. Apabila penjumlahan vektor p₁ dan p₂ yang membentuk sudut α adalah p, maka persamaannya sebagai berikut:

Impuls

Momentum yang dimiliki suatu benda tidak selamanya sama. Perubahan kecepatan menunjukkan bahwa momentum berubah. Perubahan momentum terjadi karena adanya impuls. Impuls merupakan hasil kali antara gaya dengan waktu selama gaya tersebut bekerja pada benda. Sehingga impuls dapat dirumuskan sebagai berikut:

F = m . a

Keterangan:
F = gaya (N)
m = massa (kg)
a = percepatan (m/s²)

Impuls juga termasuk besaran vektor. Sehingga impuls dapat dirumuskan sebagai berikut:

I = F.Δt

Keterangan:
F          = gaya (N)
Δt        = selisih waktu (s)
I           = impuls (Ns)

Hubungan Momentum dan Impuls

Hubungan momentum dan impuls dinyatakan dalam persamaan sebagai berikut:

I = Δp

F.Δt = m(v_t – v)

Keterangan :
I           = impuls (Ns)
Δp        = perubahan momentum (Ns)
m         = masa benda (kg)
v_t         = kecepatan akhir (m/s)
v         = kecepatan awal (m/s)

Hukum Kekekalan Momentum

Hukum kekekalan momentum menyatakan bahwa jika gaya luar yang bekerja pada suatu sistem adalah nol maka momentum linear total sistem tersebut akan tetap konstan. Dengan demikian, momentum benda sebelum tumbukan sama dengan momentum benda setelah tumbukan. Jika pada sistem interaksi bekerja gaya luar (gaya-gaya yang diberikan oleh benda lain di luar sistem) dan total sistemnya tidak nol, maka momentum total sistem tidak kekal. Secara matematis hukum kekekalan momentum dapat ditulis:

P_sebelum = P_setelah

P₁ + P₂ = P₁’ + P₂’

m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’

Keterangan:
p _sebelum = momentum sebelum tumbukan
p _setelah = momentum setelah tumbukan
m₁ = massa benda pertama
m₂ = massa benda kedua
v₁ = kecepatan awal benda pertama
v₂ = kecepatan awal benda kedua
v₁^’ = kecepatan akhir benda pertama
v₂^’ = kecepatan akhir benda kedua

Koefisien Restitusi (e)

Koefisien restitusi adalah negatif perbandingan antara kecepatan relatif sesaat sesudah tumbukan dengan kecepatan relatif sesaat sebelum tumbukan. Koefisien restitusi jika dituliskan dalam persamaan matematis sebagai berikut:

Nilai koefisien restitusi adalah terbatas, yaitu 0 ≤ e ≤ 1

Jenis-jenis Tumbukan

1. Tumbukan Lenting (Elastis) Sempurna
   Tumbukan lenting sempurna terjadi antara dua benda atau lebih yang energi kinetiknya setelah tumbukan tidak ada yang hilang dan momentum linear totalnya tetap. Untuk tumbukan lenting sempurna, kecepatan relatif sesaat sesudah tumbukan sama dengan minus kecepatan relatif sesaat sebelum tumbukan.

   1. Berlaku hukum kekekalan momentum
      m₁v₁ + m₂v₂ = m₁v₁^’ + m₂v₂^’
   2. Berlaku hukum kekekalan energi kinetik
      ½ m₁(v₁)² + ½m₂(v₂)² = ½ m₁(v₁^’ )² + ½m₂(v₂^’ )²
   3. Koefisien restitusi (e) = 1

2. Tumbukan Tidak Elastis/ Tidak Lenting Sama Sekali
   Tumbukan ini terjadi antara dua benda atau lebih yang energi kinetiknya setelah tumbukan hilang karena berubah menjadi panas, bunyi, atau bentuk energi lainnya. Tumbukan tidak elastis terjadi apabila partikel-partikel yang bertumbukan menempel bersama-sama setelah terjadi tumbukan. Momentum benda sebelum dan sesudah tumbukan adalah tetap (konstan).

   1. Berlaku hukum kekekalan momentum, dengan V₁^’= V₂^’ = V
      m₁v₁ + m₂v₂ = (m₁+ m₂)v^’
   2. Koefisien restitusi (e) = 0

3. Tumbukan Lenting (Elastis) Sebagian
   Pada tumbukan lenting sebagian terjadi antara dua benda atau lebih yang sebagian energi kinetiknya hilang setelah terjadi tumbukan karena berubah menjadi panas, bunyi, atau bentuk energi lainnya. Tumbukan lenting sebagian terjadi apabila partikel-partikel yang bertumbukan tidak menempel bersama-sama setelah terjadi tumbukan. Momentum benda sebelum dan sesudah tumbukan adalah tetap (konstan).

   1. Berlaku hukum kekekalan momentum
      m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’
   2. Koefisien restitusi (e) = 0 < e < 1

Koefisien Restitusi Benda Jatuh

Sebuah bola dijatuhkan dari ketinggian h₁ ke lantai. Setelah sampai di lantai, bola dipantulkan hingga mencapai ketinggian h₂, dengan h₂ < h₁. Pemantulan ini berlangsung berulang-ulang dengan ketinggian yang semakin berkurang.

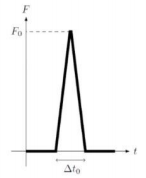
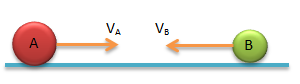
Soal No.1 (UTBK 2019)

Sebuah benda A bermassa m_A bergerak sepanjang sumbu x positif dengan laju konstan. Benda tersebut menumbuk benda B bermassa m_B yang diam. Selama tumbukan, gaya interaksi yang dialami benda B ditunjukkan dalam gambar. Jika laju benda A setelah bertumbukan adalah v_A, lajunya mula-mula adalah…

PEMBAHASAN :
Momentum adalah ukuran kesulitan dalam menghentikan benda P = mv. Contoh momentum adalah tumbukan. Pada tumbukan berlaku hukum kekekalan momentum artinya jumlah momentum sebelum dan sudah tumbukan adaalah sama.
P_o = P’
m_Av_A + m_B v_B = m_AV_A’ + m_B V_B’
Sedangkan impuls merupakan istilah ini) digunakan pada kondisi suatu benda yang dikenai gaya (F) dalam waktu (Δt) singkat.  Besarnya Impuls
I = F Δt
I = Luas yang dilingkupi pada grafik F-t
I = ΔP = mv_{2 ­}– mv₁
Untuk kasus di soal di atas v₂ = v_a dan v₁ = v_o dengan demikian:
I = ΔP = mv_{2 ­}– mv₁
Luas yang dilingkupi pada grafik F-t = mv_{2 ­}– mv₁
Dari grafik luasnya adalah luas segitiga yaitu dengan demikian:

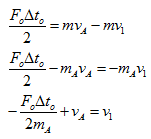
Jawaban B

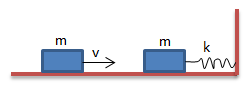
Soal No.2 (SBMPTN 2014)

Benda bermassa m berada pada bidang licin terikat pada pegas dengan tetapan k. Benda lain juga bermassa m mendekati dan menumbuk benda pertama dengan kecepatan v seperti ditunjukan pada gambar. Setelah tumbukan, kedua benda saling menempel dan bersama – sama bergetar dengan pegas. Amplitudo getaran tersebut adalah …

PEMBAHASAN :
Benda yang terikat pada pegas pada mulanya tidak memiliki kecepatan. Terjadi tumbukan,  kedua benda saling menempel dengan tumbukan tidak lenting sama sekali. Adapun kecepatan setelah tumbukan sebagai berikut:
Persamaan 1:
m₁v₁ + m₂v₂ = (m₁ + m₂)v’
v + m(0) = (m + m)v’
v’ = v/2

Persamaan 2:
Untuk benda pegas terjadi hubungan hukum kekekalan energi mekanik:
Em₁ = Em₂
Ep₁ + Ek₁ = Ep₂ + Ek₂
0 + ½mv² = ½ky² + 0
½ m(v/2)² = ½ ky²
Menghitung besarnya amplitudo → Hubungan penjumlahan energi kinetik dan energi potensial sehingga memperoleh besar energi mekanik.
E_m = Em₂
½kA²  = ½ mv² + ½ ky²
Nilai ½ ky² = ½ mv² + ½ ky²

Dari persamaan 2 dan persamaan 1 diperoleh persamaan sebagai berikut:
½kA² = ½ m(v/2)² + ½ m(v/2)²

Jawaban : D

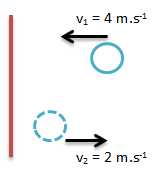
Soal No.3 (UN 2014)

Bola bermassa 20 gram dengan kecepatan v₁ = 4 m/s ke kiri. Setelah membentur tembok bola memantul dengan kecepatan v₂ = 2 m/s ke kanan. Besar impuls yang dihasilkan adalah … Ns

1. 0,24
2. 0,12
3. 0,08
4. 0,06
5. 0,04

PEMBAHASAN :
Diketahui:
m = 20 gram = 0,02 kg
v₁ = 4 m/s ke kiri = – 4 m/s
v₂ = 2 m/s ke kanan
Ditanyakan: Besarnya impuls (I)?
I = Δp
I = m(v₂ – v₁)
I = 0,02(2 – (-4)) = 0,12 Ns
Jawaban : B

Soal No.4 (UMPTN 1999)

Jika dua benda mempunyai momentum sama, tetapi massa berbeda maka benda yang bermassa lebih besar mempunyai energi kinetik yang lebih besar.

PEMBAHASAN :
Rumus untuk menghitung energi kinetik sebagai berikut: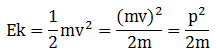

Dari rumusan di atas, diketahui bahwa energi kinetik berbanding lurus dengan kuadrat momentum (p²) dan berbanding terbalik dengan massa (m). Oleh karena itu, pernyataan dan alasan salah.
Jawaban : E

Soal No.5 (UN 2014)

Sebuah bola dari ketinggian h = 200 cm, setelah menyentuh lantai bola memantul seperti pada gambar.

Bila ketinggian pantulan pertama 1/4 h, massa bola 150 gram. Koefisien restitusi bola adalah …

1. 1/2
2. 2/3
3. 3/4
4. 4/3
5. 5/4

PEMBAHASAN :
Diketahui:
h = 200 cm
h₁ = ¼ h = ¼ (200) = 50 cm
m = 150 gram
Ditanyakan: koefisien restitusi bola?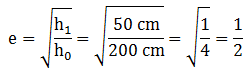

Jawaban : A

Soal No.6 (SPMB 2003)

Sebuah bola bermassa 0.3 kg bergerak dengan kecepatan 2 m/s menumbuk sebuah bola lain bermassa 0,2 kg yang mula-mula diam. Jika setelah tumbukan bola pertama diam maka kecepatan bola kedua adalah ….

1. 6 m/s
2. 5 m/s
3. 4 m/s
4. 3 m/s
5. 2 m/s

PEMBAHASAN :
Diketahui:
m₁ = m₁^’ = 0,3 kg
m₂ = m₂^’ = 0,2 kg
v₁ = 2 m/s
v₂ = v₁^’ = 0
Ditanyakan: Kecepatan bola kedua setelah tumbukan (v₂’)?
m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’
(0,3)(2) + (0,2)(0) = (0,3)(0) + (0,2)v₂’
0,6 + 0 = (0,2)v₂’
v₂’ = 3 m/s
Jawaban : D

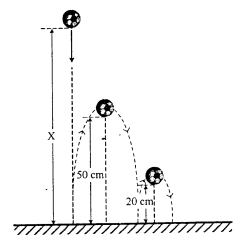
Soal No.7 (UN 2014)

Sebuah bola dijatuhkan dari ketinggian X seperti pada gambar berikut.

Jika ketinggian bola pada saat pantulan pertama 50 cm dan pantulan kedua 20 cm, maka besar X adalah … cm.

1. 60
2. 70
3. 100
4. 125
5. 150

PEMBAHASAN :

Jawaban : D

Soal No.8 (UMPTN 1992)

Dua buah benda titik bermassa m₁ = 5 kg dan m₂ = 6 kg terletak berdekatan pada bidang datar licin. Sistem ini mendapat impuls gaya hingga kedua benda bergerak masing – masing dengan kelajuan v₁ = 1 m/s dan v₂ = 2 m/s dengan arah tegak lurus . Besarnya impuls gaya yang bekerja pada sistem adalah ….. Ns

1. 5
2. 7
3. 12
4. 13
5. 17

PEMBAHASAN :
Diketahui:
m₁ = 5 kg
m₂ = 6 kg
v₁ = 1 m/s
v₂ = 2 m/s
Sudut = 90 (arah tegak lurus)
Ditanyakan: Besarnya impuls (I)?
Nilai momentum yang dapat dihitung ketika kedua benda yang akan bergerak dan membentuk arah tegak lurus dengan rumus

karena Impuls memiliki nilai sama dengan perubahan momentum.
Hubungan impuls dengan momentum: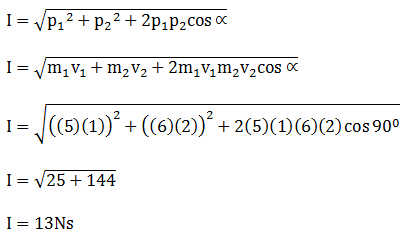

Jawaban : D

Soal No.9 (UN 2014)

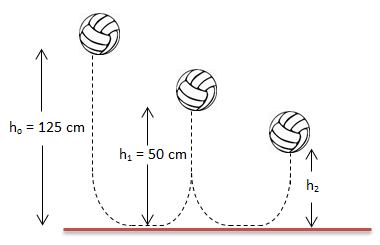
Sebuah bola dijatuhkan dari ketinggian tertentu seperti gambar berikut. Pada saat pemantulan pertama bola mencapai ketinggian 50 cm. Bola tersebut terpantul untuk kedua kalinya pada ketinggian h₂, yaitu sebesar … cm

PEMBAHASAN :

Jawaban : B

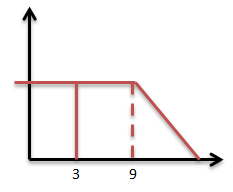
Soal No.10 (UMPTN 1991)

Grafik tersebut menyatakan hubungan gaya F yang bekerja pada benda yang bermassa 3 kg terhadap waktu t selama gaya itu bekerja pada benda. Bila benda mula – mula diam, maka kecepatan akhir benda dalam m/s adalah …

1. 5
2. 10
3. 15
4. 20
5. 25

PEMBAHASAN :
Diketahui:
m = 3 kg
Ditanyakan: Kecepatan akhir benda (v_t)?
Impuls merupakan perubahan momentum, maka I = Δp → F Δt = m Δv
Gerakan benda membentuk bidang trapesium, sehingga:
Luas Trapesium = m Δv

30 = 3Δv
Δv = 10 m/s
v_t – v = 10 m/s
v_t – 0 = 10 m/s
v_t = 10 m/s
Jawaban : C

Soal No.11 (UN 2013)

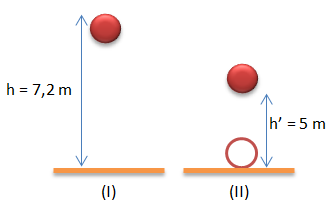
Bola bermassa 2 kg dijatuhkan dari ketinggian h di atas lantai sehingga mencapai ketinggian h’. Jika g = 10m/s², impuls yang bekerja pada benda adalah … Ns

1. 44
2. 9,6
3. 8,0
4. 5,4
5. 4,8

PEMBAHASAN :
Pada gambar (i) sebuah bola dijatuhkan dari ketinggian tertentu, sehingga kecepatan sebelum pantulan sebagai berikut:
Diketahui:
g = 10m/s²
h = 7,2 m

Pada gambar (ii) bola memantul secara vertikal ke bawah sehingga kecepatan setelah pantulan sebagai berikut:
Diketahui:
g = 10m/s²
h = 5 m

v₁ arahnya ke bawah maka nilainya negatif, v₁ = – 12 m/s
v₂ arahnya ke atas maka nilainya positif, v₂ = 10 m/s
m = 2 kg
Sehingga besarnya impuls sebagai berikut:
I = m(v₂ – v₁)
I = (2)(10 – (-12))
I = 44 Ns
Jawaban : A

Soal No.12 (UMPTN 1992)

Sebuah benda bermassa 2,5 kg digerakkan mendatar di meja licin dari keadaan diam oleh sebuah gaya mendatar F yang berubah terhadap waktu menurut F = 80 + 5t, dengan t dalam sekon dan F dalam Newton. Pada saat t = 2 sekon maka …

(1). kecepatan benda 68 m/s

(2). percepatan benda 36 m/s²

(3). momentum benda 170 kg m/s

(4). energi kinetik benda 5780 Joule

PEMBAHASAN :
Diketahui:
m = 2,5 kg
F = 80 + 5t
t = 2 sekon
Pembuktian:
Pernyataan 1

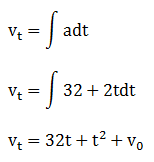
Dengan benda mula-mula diam (v = 0) dan (t = 2 sekon) sehingga kecepatannya:
v_t = 32t + t² + v₀ = 32(2) + (2)² + 0 = 68 m/s → Pernyataan benar

Pernyataan 2

Pernyataan 3
p = mv = (2,5)(68) = 170 kg m/s → Pernyataan benar

Pernyataan 4
EK = ½ mv² = ½ mv² = 5780 J → Pernyataan benar
Jawaban : E

Soal No.13 (UN 2013)

Dua bola bermassa m_A = 4 kg dan m_B = 2 kg bergerak berlawanan arah seperti gambar berikut. Kedua bola kemudian bertumbukan dan setelah tumbukan A dan B berbalik arah dengan kelajuan berturut- turut 1 m/s dan 6 m/s. Kelajuan B sebelum tumbukan adalah … m/s

1. 4
2. 6
3. 8
4. 10
5. 12

PEMBAHASAN :
Diketahui:
m_A = 4 kg
m_B = 2 kg
v_A = 6 m/s
v_A^’ = 1 m/s
v_B^’ = 6 m/s
Ditanyakan:
kelajuan B sebelum tumbukan (v_B)?
v_B = arahnya ke kiri maka nilainya negatif
m_Av_A + m_Bv_B = m_Av_A^’ + m_Bv_B^’
(4)(6) + (2)(- v_B) = (4)(-1) + (2)(6)
24 – 2v_B = – 4 + 12
2v_B = 16
v_B = 8 m/s
Jawaban : C

Soal No.14 (UMPTN 1994)

Sebuah benda bergerak dengan momentum sebesar p. Tiba – tiba benda itu pecah menjadi 2 bagian yang masing – masing besar momentumnya p₁ dan p₂ dalam arah yang saling tegak lurus sehingga …

1. p = p₁ + p₂
2. p = p₁ – p₂
3. p = p₂ – p₁
4. p = (p₁² + p₂²)^1/2
5. p = (p₁² + p₂²)

PEMBAHASAN :
Besarnya perubahan momentum ketika hasil tumbukan dalam arah saling tegak lurus maka rumusan yang dapat kita peroleh adalah sebagai berikut:

Jawaban : D

Soal No.15 (UN 2013)

Bola bekel bermasa 200 gram dijatuhkan dari ketinggian 80 cm tanpa kecepatan awal. Setelah menumbuk lantai bola bekel memantul kembali dengan kecepatan 1 m/s. Besar  impuls pada bola saat mengenai lantai adalah… Ns

1. 1,6
2. 1,5
3. 1,0
4. 0,8
5. 0,6

PEMBAHASAN :
Diketahui:
m = 200 gram = 0,02 kg
h = 80 cm
v₂ = 1 m/s
Ditanyakan: Impuls (I) ?
Untuk menghitung kecepatan sebelum tumbukan (v₁):

v₁ = bernilai negatif karena arahnya ke bawah, jadi v₁ = – 4m/s
Sehingga besarnya impuls dapat dihitung sebagai berikut:
I = ∆p
I = m(V₂ – V₁)
I = (0,2)(1-(-4)) = 1,0 N_s
Jawaban : C

Soal No.16 (UMPTN 1991)

Sebuah granat yang diam tiba – tiba meledak dan pecah menjadi 2 bagian yang bergerak dalam arah berlawanan. Perbandingan massa kedua bagian itu adalah m₁ : m₂ = 1 : 2. Bila energi yang dibebaskan adalah 3 x 10⁵ joule maka perbandingan energi kinetik pecahan granat pertama dan kedua adalah ….

1. 1 : 1
2. 2 : 1
3. 1 : 3
4. 5 : 1
5. 7 : 5

PEMBAHASAN :
Diketahui:
m₁ : m₂ = 1:2 → m₂ = 2m₁ dengan mula-mula diam.
Hukum kekekalan momentum yang berlaku adalah sebagai berikut:
0 = m₁ v₁’ + m₂v₂’
0 = m₁ v₁ + 2m₁ v₂’
-m₁ v₁ = 2m₁ v₂’
-v₁ = 2v₂’
v₁ = -2v₂’ → v₁’ dan v₂’ berlawanan arah

Maka perbandingan Ek₁ dan Ek₂ sebagai berikut: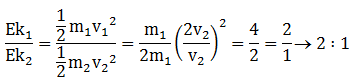

Jawaban : B

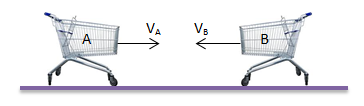
Soal No.17 (UN 2011)

Dua troli A dan B masing-masing 1,5 kg bergerak saling mendekat dengan v_A = 4 m.s^-1 dan v_B = 5 m.s^-1 seperti pada gambar. Jika kedua troli bertumbukan tidak lenting sama sekali maka kecepatan kedua troli sesudah bertumbukan adalah …

1. 4,5 m.s^-1 ke kanan
2. 4,5 m.s^-1 ke kiri
3. 1,0 m.s^-1 ke kiri
4. 0,5 m.s^-1 ke kiri
5. 0,5 m.s^-1 ke kanan

PEMBAHASAN :
Diketahui:
m_A = m_B = 1,5 kg
v_A = 4 m.s^-1 ke kanan, bernilai positif
v_B = 5 m.s^-1 ke kiri, bernilai negatif

Tumbukan tidak elastis, rumusan yang sesuai:
m_Av_A + m_Bv_B = (m_A + m_B) v’
1,5(4) + 1,5(-5) = (3) v’
6 – 7,5 = 3v’
v’ = – 0,5 m.s^-1
Sehingga v_A = v_B = v’ = – 0,5 m.s^-1 (bernilai negatif karena arahnya ke kiri)
Jawaban : D

Soal No.18 (UMPTN 1992)

Sebuah bola A yang mempunyai momentum p bertumbukan dengan bola lain B hingga setelah tumbukan momentum bola A tersebut menjadi 3p. Perubahan momentum bola B adalah …

1. 2p
2. -2p
3. -3p
4. 4p
5. p

PEMBAHASAN :
Diketahui:
p_A = p
p_A’ = 3p
Ditanyakan: Perubahan momentum bola B (p_B’ – p_B)?

Hukum kekekalan momentum yang berlaku sebagai berikut:
p_A + p_B = p_A’ + p_B’
p_B’ – p_B = p_A + p_A’
p_B^’ – p_B = p – 3p  = -2p
Jawaban : B

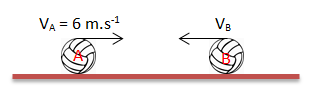
Soal No.19 (UN 2010)

Perhatikan gambar!

1. (1) saja
2. (2) saja
3. (3) saja
4. (1) dan (3)
5. (2) dan (3)

PEMBAHASAN :
Diketahui:
m_A = m_B
v_A = 5 m/s
v_B = 0 (diam)

Persamaan 1:
Hukum kekekalan momentum
m_Av_A + m_Bv_B = m_Av_A^’ + m_Bv_B^’
5 + 0 = v_A^’ + v_B^’
v_A^’ + v_B^’ = 5

Persamaan 2:
Koefisien restitusi e = 1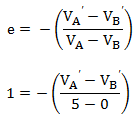

v_A^’ – v_B^’   = – 5

Dari persamaan (1) dan (2) diperoleh nilai:
v_A^’ = 0 (diam ), v_B^’ = 5 m/s → hal ini membuktikan bahwa pernyataan (1) benar.
Apabila tumbukan tidak lenting sama sekali, maka:
m_Av_A + m_Bv_B = (m_A + m_B ) v’
5m + 0 = (2m) v’
v’ = 2,5 m/s
Jadi besarnya kecepatan setelah tumbukan diketahui sebesar:
v_A = v_B = v’= 2,5 m/s
Jawaban : D

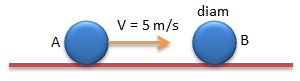
Soal No.20 (UMPTN 1994)

Bola A bergerak lurus dan mempunyai momentum mv menumbuk bola B yang bergerak pada garis lurus yang sama. Jika setelah tumbukan bola A mempunyai momentum -3mv maka pertambahan momentum bola B adalah ….

1. 2mv
2. -2mv
3. 3mv
4. -4mv
5. 4mv

PEMBAHASAN :
Diketahui:
p_A = mv
p_A’ = -3mv
Ditanyakan: pertambahan momentum bola B (p_B’ – p_B)?

Hukum kekekalan momentum yang berlaku sebagai berikut:
p_A + p_B = p_A’ + p_B’
p_B’ – p_B = p_A – p_A’
p_B’ – p_B = mv – (-3mv) = 4mv
Jawaban : E

Soal No.21 (UN 2009)

Dua buah benda bermassa sama bergerak pada satu garis lurus saling mendekati seperti pada gambar!

Jika v₂^’ adalah kecepataan benda (2) setelah tumbukan ke kanan dengan laju 5 m.s^-1, maka besar kecepatan  ’(1) setelah tumbukan adalah ….

1. 7 m.s^-1
2. 9 m.s^-1
3. 13 m.s^-1
4. 15 m.s^-1
5. 17 m.s^-1

PEMBAHASAN :
Diketahui:
m₁ = m₂
V₁ = 8 m.s^-1
V₂ = -10 m.s^-1
V₂‘ ₌ 5 m.s^-1 
Ditanyakan: kecepatan benda (1) setelah tumbukan (v₁’) ?

Hukum kekekalan momentum
m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’
8 + (-10) = v₁’+ 5
v₁’ = -7 m.s^-1 (ke arah kiri)
Jawaban : A

Soal No.22 (UMPTN 1996)

Dua benda yang bertumbukan tidak lenting sama sekali mempunyai kecepatan sama setelah tumbukan.

PEMBAHASAN :

• Pernyataan di atas benar karena dua benda yang bertumbukan dengan tumbukan tidak lenting sama sekali akan menyebabkan benda saling berimpit setelah tumbukan sehingga kedua benda tersebut menjadi memiliki kecepatan yang sama.
• Alasan benar karena dari ketiga jenis tumbukan, yaitu tumbukan lenting sempurna, tumbukan lenting sebagian, dan tumbukan tidak lenting sama sekali selalu berlaku hukum kekekalan momentum.
• Penjelasan di atas, pernyataan dan alasan tidak mempunyai hubungan sebab akibat.

Jawaban : B

Soal No.23 (UN 2008)

Pada permainan bola kasti, bola bermassa 0,5 kg mula-mula bergerak dengan kecepatan 2 m.s^-1. Kemudian bola tersebut di pukul dengan gaya F berlawanan dengan gerak bola sehingga kecepatan bola berubah menjadi 6 m.s^-1. Bila bola bersentuhan dengan pemukul selama 0,01 sekon maka perubahan momentumnya adalah …

PEMBAHASAN :
Diketahui:
m = 0,5 kg
v₁ = 2 m/s
v₂ = 6 m/s
Ditanyakan: Perubahan momentumnya (Dp)?

Perubahaan momentum dapat dihitung dengan persamaan berikut:
∆p = m∆v
∆p = m(V₂ – V₁)
∆p = 0,5(6 – 2)
∆p = 2kg.m.s^-1
Jawaban : E

Soal No.24 (Matematika Dasar UM UGM 2013)

Sebuah benda yang mula-mula diam di tumbuk oleh benda lain. Bila massa kedua benda sama dan tumbukkan lenting sempurna maka …

PEMBAHASAN :
Jika benda mengalami tumbukkan lenting sempurna maka berlaku hukum kekekalan momentum dan hukum kekekalan energi kinetik, dengan koefisien restitusi (e = 1).  Sedangkan ketika dua benda memiliki massa yang sama maka setelah tumbukkan yang kecepatan benda yang menumbuk sama dengan nol dan benda yang ditumbuk menjadi bergerak dengan kecepatan yang sama dengan kecepatan benda pertama sebelum menumbuk.
Jawaban : E

Soal No.25 (UN 2005)

Dua bola masing – masing mempunyai massa m₁ = 6 kg dan m₂ = 4 kg bergerak pada suatu garis lurus dalam arah berlawanan dengan kecepatan v₁ = 4 m/s dan v₂ = 6 m/s, seperti gambar berikut, kemudian bertumbukan tidak lenting sama sekali.

Kecepatan masing – masing benda sesaat setelah tumbukan adalah …

1. 0 m/s
2. v₁’= 0 m/s dan v₂’ = 2 m/s searah
3. v₁’= 4 m/s dan v₂’= 6 m/s berlawanan arah
4. v₁’= 6 m/s dan v₂’ = 3 m/s berlawanan arah
5. v₁’= 12 m/s dan v₂’ = 0 m/s berlawanan arah

PEMBAHASAN :
Diketahui:
m₁ = 6 kg
m₂ = 4 kg
v₁ = 4 m/s (arah ke kanan)
v₂ = – 6 m/s (arah ke kiri)
Ditanyakan: Kecepatan benda sesaat setelah tumbukan (v^’)?

Persamaan untuk tumbukan tidak lenting sama sekali:
m₁v₁ + m₂v₂ = (m₁ + m₂)v’
6(4) + 4(-6) = (6 + 4)v’
10 v’ = 0
Maka v’ = 0 m/s
Jawaban : A

Soal No.26 (UMPTN 1992)

Benda A (5 kg) dan benda B (1 kg) bergerak saling mendekati dengan kecepatan masing-masing  2 m/s dan 12 m/s. setelah tumbukkan kedua benda saling menempel. Kecepatan sesaat setelah benda bertumbukkan adalah …

1. 0,25 m/s searah dengan gerak benda A semula
2. 0,33 m/s berlawanan arah dengan gerak benda A semula
3. 0,45 m/s searah dengan gerak benda A semula
4. 0,45 m/s berlawanan arah dengan gerak A semula
5. 0,55 m/s searah dengan gerak benda A semula

PEMBAHASAN :
Diketahui:
m_A = 5 kg
v_A = 2 m/s
m_B = 1 kg
v_B = – 12 m/s
Ditanyakan: Kecepatan sesaat setelah benda bertumbukkan (V’)?

Hukum kekekalan momentum untuk benda saling menempel sebagai berikut :
m_Av_A + m_B v_B = (m_A + m_B)v’
(5)(2) + (1)(-12) = (5+1)V’
-2 = 6 V’
v’ = – 1/3 = – 0,33 m/s
Jawaban : B

Soal No.27 (UN 2005)

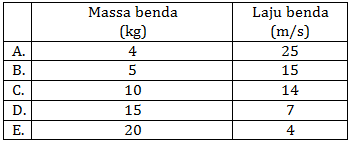
Pada percobaan momentum di laboratorium fisika, untuk mengetahui hubungan antara perubahaan momentum dengan gaya maka dilakukan percobaan dengan menggunakan massa yang berbeda–beda dan kecepatan berbeda juga didapatkan data seperti tabel berikut. Di tabel tersebut buatlah kesimpulan, benda mana yang menghasilkan gaya paling besar ketika benda menumbuk dinding dan setelah tumbukan langsung berhenti?

PEMBAHASAN :

Jawaban : C

Soal No.28 (UMPTN 2000)

Balok bermassa m₁ (2kg) dan m₂ (4kg) saling mendekati di atas bidang horizontal yang licin. Kelajuan awal m₁ dan m₂ adalah v₁ = 5 m/s dan v₂ = 10 m/s. Kedua balok saling tumbukan maka momentum linear…

PEMBAHASAN :
Diketahui:
m₁ = 2 kg
m₂ = 4 kg
v₁ = 5 m/s
v₂ = – 10 m/s

Pernyataan (1) sistem adalah 30 kg m/s
Hukum kekekalan momentum:
P = m₁v₁ + m₂v₂
P = (2)(5) + (4)(-10) = -30 kg m/s ⇒ pernyataan benar

Pernyataan (2) balok kedua 30 kg m/s jika kelajuan balok pertama menjadi nol
Jika p₁’ = 0 maka besarnya momentum balok kedua setelah tumbukan:
p = p₁’ + p₂’
-30 = 0 + p₂’
p₂’ = – 30 kg m/s ⇒ pernyataan benar

Pernyataan (3) balok kedua 20 kg m/s jika kelajuan balok pertama  5 m/s ke kiri
p = p₁’ + p₂’
P = m₁v₁’ + p₂’
-30 = (2)(-5) + p₂’
p₂’= – 20 kg m/s ⇒ pernyataan benar

Pernyataan (4) balok pertama 30 kg m/s ketika kelajuan balok kedua nol
Jika p₂’ = -0 sehingga besarnya momentum balok pertama setelah tumbukan:
p = p₁’ + p₂’
-30 = p₁’ + 0
p₁’ = – 30 kg m/s ⇒ pernyataan benar
Jawaban : E

Soal No.29 (UN 2004)

Sebutir peluru yang massanya 0,01 kg ditembakan pada suatu ayunan balistik bermassa 1kg sehingga peluru bersarang di dalamnya dan ayunan naik setinggi 0,2 m dari kedudukan semula. Jika g =  10 m/s², kecepatan peluru yang ditembakan adalah …

1. 302 m/s
2. 282 m/s
3. 240 m/s
4. 202 m/s
5. 101 m/s

PEMBAHASAN :
Diketahui:
m_peluru = 0,01 kg
m_balistik = 1 kg
h = 0,2 m
g = 10 m/s²
Ditanyakan: Kecepatan peluru yang ditembakkan (v_peluru) ?

Berlaku hukum kekekalan energi mekanik pada kejadian ini: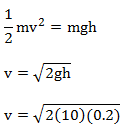

v = 2 m/s ⇒ kecepatan peluru dan balistik setelah bertumbukan
Kejadian ini termasuk tumbukan tidak lenting sama sekali karena peluru bersarang pada balistik, dengan v_b = 0 (diam) maka berlaku:
m_peluruv_peluru + m_balistikv_balistik = (m_peluru + m_balistik) v
0,01 v_p + 0 = (1,01) 2
Sehingga, v_p = 202 m/s
Jawaban : D

Soal No.30 (SPMB 2005)

Dua buah benda A dan B bermassa sama masing-masing 2 kg saling bertumbukkan. Kecepatan sebelum tumbukan adalah v_A= 15i + 30j m/s dan v_B = -10J + 5j m/s. Kecepatan benda A setelah tumbukan adalah -5i + 20j m/s. Persentase energi kinetik yang hilang setelah tumbukan adalah …

1. 10%
2. 20%
3. 40%
4. 60%
5. 80%

PEMBAHASAN :
Diketahui:
m_A = m_B = m = 2kg
v_A= 15i + 30j m/s
v_B = -10J + 5j m/s
v_A’ = -5i + 20j m/s
Ditanyakan: Persentase energi kinetik yang hilang setelah tumbukan (∆Ek/Ek x100%)?

Hukum kekekalan momentum:
m_A v_A + m_B v_B = m_A v_A‘ + m_B v_B‘
(m)(15i + 30j) + (m)(-10i + 5j) = (m)(-5i + 20j) + mv_B’
V_B = 10i + 5j

Energi kinetik sebelum terjadi tumbukan:
Ek = Ek_A + Ek_B
Ek = ½ m v_A² + ½ m v_B²
Ek = ½ (2)[(15² + 30²) + (10² + 5²)] = 1250J

Ek setelah tumbukan
Ek = Ek_A + Ek_B
Ek = ½ mv_A² + ½ mv_B²
Ek = ½ m(v_A² + v_B²)
Ek = ½ (2)[(5² + 20²) + (10² + 15²)]
Ek = 750 J

Maka persentase energi  yang hilang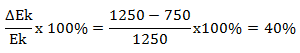

Jawaban : C

Soal No.31 (UN 2003)

Dua benda yang massanya sama masing-masing 2 kg saling mendekati dengan kecepatan 6 m/s (ke kanan) dan 2 m/s (ke kiri ). Setelah  tumbukan, kedua benda menjadi satu. Besarnya  kecepatan kedua benda setelah tumbukan adalah …

1. 2 m/s arah ke kanan
2. 4 m/s arah ke kanan
3. 2 m/s arah ke kiri
4. 4 m/s arah ke kiri

PEMBAHASAN :
Diketahui:
m_A = m_B = 2 kg
v_A = 6 m/s
v_B = – 2 m/s
Ditanyakan: Kecepatan kedua benda setelah tumbukan (v’) ?

m_Av_A + m_Bv_B = (m_A + m_B) v’
2(6) + 2(-2) = (2+2) v’
4v’ = 8 m/s
v’ = 2 m/s ⇒ nilainya positif menunjukkan pergerakan setelah tumbukan arahnya ke kanan
Jawaban : A

Soal No.32 (SBMPTN 2015)

Pada peristiwa tumbukan dua kelerang, jumlah momentum kedua kelereng tidak berubah

SEBAB

Gaya interaksi antara kedua kelereng memenuhi hukum III Newton

PEMBAHASAN :
Pada benda yang bertumbukan berlaku hukum kekekalan momentum “jika tidak ada gaya luar yang bekerja pada sistem, maka momentum total sesaat sebelum sama dengan momentum total sesudah tumbukan”. Pada hukum III Newton berlaku F aksi = – F reaksi, dimana F = ΔP/Δt. Pada tumbukan dua kelereng masing-masing kelereng mengerjakan gaya terhadap kelereng lainnya. dengan kedua gaya yang sama besar, berlawanan arah, dan bekerja pada benda yang berbeda (syarat pasangan gaya aksi dan reaksi berdasarkan hukum III Newton)Maka pernyataan benar  dan alasannya benar dan ada hubungan
Jawaban : A