Rangkuman, Contoh Soal & Pembahasan Logika Matematika

Operasi Logika

Operasi pada logika matematika ada 5, yaitu:

1. Negasi/ ingkaran ( bukan …)
   Negasi atau ingkaran apabila dari sebuah pernyataan dapat membubuhkan kata tidak benar atau dapat menyisipkan kata bukan. Jika P adalah sebuah pernyataan, maka negasi/ ingkarannya dapat ditulis  .

2. Disjungsi (… atau …)
   Disjungsi apabila pernyataan yang dibentuk dari dua pernyataan, misalkan p dan q yang dirangkaikan menggunakan kata hubung atau. Dapat dilambangkan , dibaca p atau q.

3. Konjungsi (… dan ….)
   Konjungsi apabila pernyataan yang dibentuk dari dua pernyataan, misalkan p dan q yang dirangkaikan menggunakan kata hubung dan. Dapat dilambangkan , dibaca p dan q.

5. Implikasi (jika … maka …)
   Implikasi bisa diartikan dengan pernyataan bersyarat/ kondisional, apabila pernyataan majemuk disusun dari dua buah pernyataan. Misalkan jika p maka q dilambangkan .
6. Biimplikasi/implikasi dwiarah (jika dan hanya jika …)
   Biimpikasi apabila pernyataan dapat dirangkai dengan menggunakan kata hubung “ jika dan hanya jika”. Misalkan p jika dan hanya jika q dilambangkan

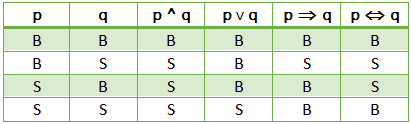
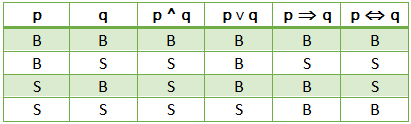
Tabel Kebenaran

Kuantor

Suatu ungkapan yang diterapkan pada kalimat terbuka dengan satu variabel dan dapat mengubahnya menjadi kalimat tertutup disebut kuantor. Ada 2 macam Kuantor, yaitu:

1. Kuantor Universal 
   Suatu pernyataan yang berlaku untuk umum, dilambangkan   dibaca “untuk semua nilai x”.
2. Kuantor Eksistensial
   Suatu pernyataan yang berlaku secara khusus, dilambangkan  dibaca “ada nilai x” atau “beberapa nilai x”.

Negasi pernyataan majemuk

Konvers, Invers, dan Kontraposisi

Hubungan nilai kebenaran dari suatu implikasi p   q diperoleh:

1. q ⇒ p disebut konvers dari p ⇒ q
2. ~ p⇒ ~ q disebut invers dari p ⇒ q
3. ~ q ⇒ p disebut kontraposisi dari p ⇒ q

Ekuivalensi

Dua pernyataan majemuk dikatakan ekuivalen jika kedua pernyataan itu mempunyai nilai kebenaran yang sama. Pernyataan  ekuivalensi ada dua, yaitu:

1. p ⇒ q ≡ ~ p v q
2. p ⇒ q ≡ ~q ⇒ p

Penarikan Kesimpulan

Proses penarikan kesimpulan dari beberapa pernyataan yang diketahui nilai kebenarannya disebut premis. cara menarik kesimpulan dari 2 premis sebagai berikut:

1. Modus Ponens (Kaidah Pengasingan)
   Premis 1 : p ⇒ q
   Premis 2 : p
   Kesimpulan : q
2. Modus Tolens (Kaidah Penolakan Akibat)
   Premis 1 : p ⇒ q
   Premis 2 : ~q
   Kesimpulan : ~p          
3. Silogisme (Sifat Menghantar atau Transitif)
   Premis 1 : p ⇒ q
   Premis 2 : q ⇒ r
   Kesimpulan : p ⇒ r

Soal No.1 (UM UGM 2009)

Ingkaran dari pernyataan “Tidak benar bahwa jika Ani lulus sekolah maka ia di belikan sepeda” adalah …

1. Ani lulus sekolah, tetapi ia tidak di belikan sepeda.
2. Ani lulus sekolah dan ia dibelikan sepeda.
3. Ani tidak lulus sekolah, tetapi ia dibelikan sepeda.
4. Ani tidak sekolah dan ia tidak dibelikan sepeda.
5. Ani tidak lulus sekolah sehingga ia tidak dibelikan sepeda.

PEMBAHASAN :
“Tidak benar bahwa jika Ani lulus sekolah, maka ia di belikan sepeda”.  Bisa diartikan sama dengan pernyataan “Jika ani tidak lulus sekolah maka Ani tidak di belikan sepeda”.
Diketahui pernyataan:
P = Ani lulus sekolah
q = Ani dibelikan sepeda
~ (~ p Þ ~ q) = ~ (p Ú ~ q) = ~ p Ù q
Maka ingkarannya menjadi “Ani tidak lulus sekolah, tetapi ia dibelikan sepeda”.
Jawaban : E

Soal No.2 (UN 2010)

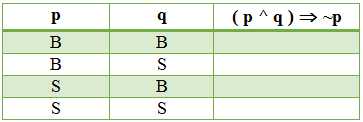
Nilai kebenaran yang tepat untuk pernyataan ( p ^ q )  ~ p pada tabel berikut adalah …

1. SBSB
2. SSSB
3. SSBB
4. SBBB
5. BBBB

PEMBAHASAN :
Tabel kebenaran untuk menentukan nilai yang tepat untuk ( p ^ q )  ~ p: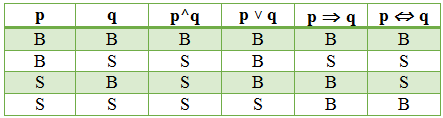

Jawaban : D

Soal No.3 (Matematika Dasar 1995)

Pertanyaan (~ p ∨ q) ∧ (p ∨ ~ q) ≡ p ⇔ q ekuivalen dengan pernyataan…

1. p ⇒ q
2. p ⇒ ~ q
3. ~ p ⇒ q
4. ~ p ⇒ ~ q
5. p ⇒ q

PEMBAHASAN :
⇔(~ p ∨ q) ∧ (p ∨ ~ q)
≡ (p ⇒ q) ∧ (~p ⇒ ~q)
≡ (p ⇒ q) ∧ (q ⇒ p)
≡ p ⇔ q
Jawaban : E

Soal No.4 (UN 2008)

Jika ~ p menyatakan negasi dari pernyataan p, dengan ~ p bernilai benar dan q bernilai salah, maka pernyataan berikut bernilai benar adalah …

1. (~ p ∨ ~ q) ∧ q
2. (p ⇒ q) ∧ q
3. (~ p ⇔ q) ∧ p
4. (p ∧ q) ⇒p
5. (~ p ∨ q) ⇒ p

PEMBAHASAN :
Diketahui:
~ p bernilai benar
q bernilai salah

Jawaban : D

Soal No.5 (Matematika Dasar SMNPTN 2009)

Diketahui tiga pernyataan berikut:
P : Jakarta ada di pulau Bali.
Q : 2 adalah bilangan prima.
R : Semua bilangan prima adalah bilangan ganjil.
Pernyataan majemuk berikut ini yang bernilai benar adalah …

1. (~ P ∨ Q) ∧ R
2. (~ Q ∨ ~ R) ∧(~ Q ∨ P)
3. (P ∧ ~ Q) ∧ (Q ∨ ~ R)
4. ~ P ⇒ R
5. ~ R ∧ ~ (Q ∧ R)

PEMBAHASAN :
Pernyataan:
P : Jakarta ada di pulau Bali.
(pernyataan salah)

Q : 2 adalah bilangan prima.
(pernyataan benar)

R : Semua bilangan prima adalah bilangan ganji.
(pernyataan salah)

Jadi, pernyataan majemuk yang benilai benar adalah
~ R ∧ ~ (Q ∧ R)

Pembuktian kebenaran:
⇔ ~ S ∧ ~ (B ∧ S)
⇔ B ∧ ~ S
⇔ B ∧ B
⇔ B
Jawaban : E

Soal No.6 (UN 2004)

Negasi dari kalimat majemuk : “Gunung Bromo di Jawa Timur atau Bunaken di Sulawesi Utara “ adalah …

1. Gunung Bromo tidak di Jawa Timur atau Bunaken tidak di Sulawesi Utara.
2. Gunung Bromo tidak di Jawa Timur dan Bunaken tidak di Sulawesi Utara.
3. Gunung Bromo di Jawa Timur dan Bunaken tidak di Sulawesi Utara.
4. Jika Gunung Bromo di Jawa Timur, maka Bunaken tidak di Sulawesi Utara
5. Jika Gunung Bromo di Jawa Timur, maka Bunaken tidak di Sulawesi Utara.

PEMBAHASAN :
Pernyataan pada soal:
p = Gunung Bromo di Jawa Timur.
q = Bunaken di Sulawesi Utara.
Pernyataan dari kalimat majemuk dapat ditulis: p ˅ q negasinya: ~ (p ˅ q) ≡ ~ p ∧ ~ q. Maka negasi dari pernyataan tersebut adalah “Gunung Bromo tidak di Jawa Timur dan Bunaken tidak di Sulawesi Utara”.
Jawaban : B

Soal No.7 (Matematika Dasar SNMPTN 2010)

Jika pernyataan “Matahari bersinar dan hari tidak hujan” bernilai benar maka pernyataan itu ekuivalen (setara) dengan pernyataan …

1. “Matahari tidak bersinar jika dan jika hanya hari hujan”.
2. “Matahari tidak bersinar dan hari tidak hujan”.
3. “Jika matahari bersinar maka hari hujan”.
4. “Matahari bersinar dan hari hujan”.
5. “Matahari tidak bersinar”.

PEMBAHASAN :
Diketahui pernyataan:
p = matahari bersinar
q = hari hujan.
”Matahari bersinar dan hari tidak hujan”, pernyataan dituliskan:  ≡ p ∧ ~ q. Pernyataan akan bernilai benar jika keduanya bernilai benar. Jadi, p benar dan ~ q benar atau q salah.
“Matahari tidak bersinar jika dan hanya jika hari hujan“, pernyataan dituliskan:  ≡ ~ p ⇔ q jadi ~ p ⇔ q pernyataan bernilai s ⇔ s hasilnya benar.
Jawaban : A

Soal No.8 (UN 2012)

Ingkaran dari pernyataan “ Jika semua mahasiswa berdemonstrasi maka lalu lintas macet” adalah …

PEMBAHASAN :
Diketahui pernyataan:
p = Semua mahasiswa berdemonstrasi
q = Lalu lintas macet
Pernyataan tersebut dilambangkan: p ⇒ q ingkarannya: ~ (p ⇒ q) ≡ ~ (~ p ˅ q) p ∧~ q. Maka ingkaran dari pernyataan di atas adalah “Semua mahasiswa berdemonstrasi dan lalu lintas tidak macet”.
Jawaban : C

Soal No.9 (Matematika Dasar UM UNDIP 2009)

Ingkaran yang benar dari pernyataan majemuk “saya lulus UM dan saya gembira” adalah …

1. Tidak benar bahwa saya lulus UM dan saya gembira.
2. Saya tidak lulus UM dan saya tidak gembira.
3. Saya lulus UM dan saya tidak gembira.
4. Saya tidak lulus UM atau saya gembira.
5. Jawaban salah semua.

PEMBAHASAN :
Diketahui pernyataan:
p = saya lulus UM.
q = saya gembira.
Saya lulus UM dan saya gembira, pernyataan dituliskan: (p ∧ q). Ingkaran p ∧ q adalah ~ (p ∧ q) ≡ ~ p ∨ ~ q.
Maka, ingkarannya adalah “saya tidak lulus UM atau saya tidak gembira”.
Jawaban : E

Soal No.10 (UN 2002)

Ingkaran dari  √4 < 4 jika dan hanya jika sin 45^o < sin 60^o adalah ..

1. √4 ≤ 4 jika dan hanya jika sin 45^o < sin 60^o
2. √4 < 4 jika dan hanya jika sin 45^o ≥ sin 60^o
3. √4 ≥ 4 jika dan hanya jika sin 45^o > sin 60^o
4. √4 ≥ 4 jika dan hanya jika sin 45^o ≥ sin 60^o
5. √4 ≥ 4 jika dan hanya jika sin 45^o > sin 60^o

PEMBAHASAN :
Diketahui:
p =  √4 < 4
q = sin 45^o < sin 60^o
Pernyataan “√4 < 4 jika dan hanya jika 45^o < sin 60^o” dilambangkan dengan  p ⇔ q sehingga ~ (p ⇔ q) ≡ p ⇔ ~ q. Maka ingkarannya adalah √4 < 4 jika dan hanya jika sin 45^o ≥ sin 60^o
Jawaban : B

Soal No.11 (Matematika IPA UM UNDIP 2009)

Negasi dari pernyataan (∀x)[a(x) ⇒ b(x)] adalah …

1. (Ex)[a(X) ⇒ ~ b(x)]
2. (Ex)[a(x) ∧ b(x)]
3. (Ex)[~a(x) ∧ ~ b(x)]
4. (Ex)[a(x) ⇒ b(x)]
5. (Ex)[a(x) ∧ ~ b(x)]

PEMBAHASAN :
Diketahui:
Negasi dari pernyataan (∀x)[a(x) ⇒ b(x)] dapat dijabarkan:
(∀x)[a(x) ⇒ b(x)]
~(∀x)[~(~a(x) ∨ b(x))]
(Ex)[A(x) ∧ ~ b(x)]
Jawaban : E

Soal No.12 (UN 1995)

Kontraposisi dari pernyataan “Jika semua siswa menyukai matematika maka guru senang mengajar” adalah …

1. Jika guru senang mengajar maka ada siswa yang tidak suka matematika.
2. Jika tidak semua siswa menyukai matematika maka guru tidak senang mengajar.
3. Jika guru tidak senang mengajar maka ada siswa yang suka matematika.
4. Jika semua siswa menyukai matematika, maka guru tidak senang mengajar.
5. Jika guru tidak senang mengajar maka ada siswa yang tidak suka matematika.

PEMBAHASAN :
Diketahui pernyataan:
p = Semua siswa menyukai matematika.
q = Guru senang mengajar.
Pada pernyataan “Jika semua siswa menyukai matematika maka guru senang mengajar” dilambangkan p ⇒ q.
Kontraposisi p ⇒ q adalah ~ q ⇒ ~ p. Maka kontraposisinya adalah jika guru tidak senang mengajar maka ada siswa yang tidak suka matematika.
Jawaban : E

Soal No.13 (MATEMATIKA DASAR UM UNDIP 2009)

Kontraposisi dari pernyataan “Bila mahasiswa pandai maka mahasiswa lulus ujian akhir” adalah …

1. Bila mahasiswa lulus ujian akhir maka mahasiswa pandai.
2. Bila mahasiswa tidak pandai maka mahasiswa tidak lulus ujian akhir.
3. Bila mahasiswa tidak lulus ujian akhir maka mahasiswa tidak  pandai.
4. Bila mahasiswa pandai maka mahasiswa tidak lulus ujian akhir.
5. Bila mahasiswa tidak pandai maka mahasiswa lulus ujian akhir.

PEMBAHASAN :
Diketahui pernyataan:
p = Mahasiwa pandai
q = Mahasiswa lulus ujian akhir
Dari pernyataan di atas kontraposisinya p ⇒ q adalah ~ q ⇒ ~ p. Maka, “Bila mahasiswa tidak lulus ujian akhir maka mahasiwa tidak  pandai”.
Jawaban : C

Soal No.14 (UN 2001)

Ditentukan pernyataan (p ˅ ~ q) ⇒ p. Konvers dari pernyataan tersebut adalah …

1. p ⇒ (~ p ˅ q )
2. p ⇒ (p ∧ ~ q)
3. p ⇒ (q ˅ ~ q)
4. p ⇒ (p ˅ q)
5. p ⇒ (~ p ˅ ~ q)

PEMBAHASAN :
Konvers dari pernyataan (p ˅ ~ q) ⇒ p adalah p ⇒ (p ˅ ~ q)
Jawaban : C

Soal No.15 (Matematika Dasar UMPTN 2001)

Nilai x yang menyebabkan pernyataan  “Jika x² + x = 6, maka x² + 3x < 9” bernilai salah adalah …

1. -3
2. -2
3. 1
4. 2
5. 6

PEMBAHASAN :
“Apabila x² + x = 6, maka  x² + 3x < 9” akan bernilai salah bila x² + x = 6 bernilai benar dan x² + 3x < 9 bernilai salah.
Persamaan x² + x = 6 dijabarkan:
⇔ x² + x – 6 = 0
⇔ (x – 2)(x + 3) = 0
Sehingga x² + x = 6 bernilai benar bila x = 2 atau x = -3
x² + 3x < 9
⇔ x = 2 → 4 + 6 < 9 (pernyataan salah)
⇔ x = -3 → 9 – 6 < 9 (pernyataan benar)
Maka, pernyataan akan bernilai salah untuk x = 2
Jawaban : D

Soal No.16 (UN 2013)

Pernyataan yang setara dengan pernyataan “Ani tidak mengikuti pelajaran matematika atau ani mendapat tugas menyelesaikan soal-soal matematika” adalah …

1. Jika Ani mengikuti pelajaran matematika maka Ani mendapat tugas menyelesaikan soal-soal matematika.
2. Jika Ani tidak mengikuti pelajaran matematika maka Ani mendapat tugas menyelesaikan soal-soal matematika.
3. Jika Ani tidak mengikuti pelajaran matematika maka Ani tidak mendapat tugas tidak menyelesaikan soal-soal matematika.
4. Ani tidak mengikuti pelajaran matematika dan Ani mendapat tugas menyelesaikan soal-soal matematika.
5. Ani tidak mengikuti pelajaran matematika dan Ani tidak mendapat tugas menyelesaikan soal-soal matematika.

PEMBAHASAN :
Diketahui pernyataan:
P = Ani mengikuti pelajaran matematika
q  = Ani mendapat tugas menyelesaikan soal-soal matematika.

Pernyataan di atas dilambangkan sebagai berikut:
~ p ∨ q = p ⇒ q
Maka, pernyataan yang setara dengan soal adalah ”Jika Ani mengikuti pelajaran matematika maka ani mendapat tugas menyelesaikan soal-soal”.
Jawaban : A

Soal No.17 (MATEMATIKA DASAR SNMPTN 2009)

Jika x adalah peubah pada bilangan real, nilai x yang memenuhi agar pernyataan “Jika x² – 2x – 3 = 0 maka x² – x < 5” bernilai salah adalah ….

1. -1
2. 1
3. 2
4. 3
5. 4

PEMBAHASAN :
Diketahui pernyataan:
p: x² – 2x – 3 = 0
q: x² – x < 5
Pernyataan tersebut akan bernilai salah jika p benar dan q salah
Persamaan x² – 2x – 3 = 0 dijabarkan:
x² – 2x – 3 = 0
(x – 3)(x + 1) = 0
x = 3 atau  x = – 1
x² – x < 5
x = 3 → 3² – 3 < 5 (pernyataan salah)
x = -1 → (-1)² – (-1) < 5 (pernyataan benar)
Maka, yang memenuhi x = 3
Jawaban : D

Soal No.18 (UN 2014)

Pernyataan yang ekuivalen dengan pernyataan ”Jika semua siswa hadir maka beberapa guru tidak hadir” adalah…

1. Beberapa siswa tidak hadir atau beberapa guru hadir.
2. Semua siswa tidak hadir atau beberapa guru tidak hadir.
3. Beberapa siswa tidak hadir dan semua guru tidak hadir.
4. Beberapa siswa tidak hadir atau beberapa guru tidak hadir.
5. Semua siswa hadir dan beberapa guru hadir.

PEMBAHASAN :
Diketahui pernyataan:
p = semua siswa hadir
q = beberapa guru tidak hadir
Pernyataan tersebut dilambangkan sebagai berikut:
p ⇒ q = ~ p ∨ q
Maka, pernyataan yang setara adalah ”Beberapa siswa tidak hadir atau beberapa guru tidak hadir”.
Jawaban : A

Soal No.19 (Matematika Dasar UM UNDIP 2008)

Jika Adi tidak sombong maka Adi mempunyai banyak teman. Pada kenyataannya , Adi tidak mempunyai banyak teman, kesimpulan yang benar adalah…..

1. Adi pasti sombong.
2. Adi mungkin anak yang baik.
3. Adi bukan anak yang baik.
4. Adi punya beberapa teman.
5. Adi anak yang baik.

PEMBAHASAN :
Diketahui pernyataan:
p = Adi sombong
q = Adi mempunyai banyak teman
Premis 1 : ~ p ⇒ q
Premis 2 : ~q
Kesimpulan : p
Maka, kesimpulannya adalah  “Adi pasti sombong”.
Jawaban : A

Soal No.20 (UN 2013)

Pernyataan yang setara dengan “Jika setiap siswa berlaku jujur dalam UN maka nilai UN menjadi pertimbangan masuk PTN” adalah…

1. Jika ada siswa berlaku tidak jujur dalam UN maka nilai UN menjadi pertimbangan masuk PTN.
2. Jika nilai UN menjadi pertimbangan masuk PTN maka setiap siswa berlaku jujur dalam UN.
3. Jika nilai UN tidak menjadi pertimbangan masuk PTN maka ada siswa tidak berlaku jujur dalam UN.
4. Setiap siswa berlaku jujur dalam UN dan nilai UN tidak menjadi pertimbangan masuk PTN.
5. Ada siswa tidak berlaku jujur dalam UN atau nilai UN tidak menjadi pertimbangan masuk PTN.

PEMBAHASAN :
Diketahui pernyataan:
p  = setiap siswa berlaku jujur dalam UN
q  = nilai UN menjadi pertimbangan masuk PTN
Pernyataan tersebut dilambangkan:
p ⇒ q ≡ ~q ⇒ ~p
Maka, pernyataan yang setara adalah “jika nilai UN tidak menjadi pertimbangan masuk PTN maka ada siswa yang tidak berlaku jujur dalam UN”.
Jawaban : C

Soal No.21 (SNMPTN 2009)

Diberikan premis-premis sebagai berikut:
p : Jika x² ≥ 0, maka 2 merupakan bilangan prima
q : 2 bukan bilangan prima.
Kesimpulan dari kedua premis tersebut adalah …

1. x² ≥ 0
2. x² > 0
3. x > 0
4. x² < 0
5. x ≠ 0

PEMBAHASAN :
Diketahui: a = Jika x² ≥ 0 , b = 2 merupakan bilangan prima
Pernyataan:
p : a ⇒ b
q : ~b
Kesimpulan : ~a
Maka,  x² < 0
Jawaban : D

Soal No.22 (UN 2005)

PEMBAHASAN :

1. p ⇒ q ≡ ~q ⇒ ~p
   ~p       
   ∴ ~q
   Argument I merupakan modus tollens
2. p ⇒ q
   ~q ∨ r ≡ q ⇒ r
   ∴ p ⇒ r
   Argument II merupakan silogisme

Jawaban : D

Soal No.23 (SNMPTN 2011)

Jika ~ p adalah negasi dari P maka kesimpulan dari pernyataan-pernyataan:  p ⇒ q dan ~ q ∨ ~ r adalah …

1. r ∨ p
2. ~p ∨ ~r
3. ~p ⇒ q
4. ~r ⇒ p
5. ~r ⇒ q

PEMBAHASAN :
Diketahui premis:
Premis 1 : p ⇒ q
Premis 2 : ~q ∨ ~r ≡ q → ~r
Kesimpulan : p → ~r ≡ ~p ∨ ~r
Jawaban : B

Soal No.24 (UN 2012)

Ani rajin belajar maka naik kelas.
Ani dapat hadiah atau tidak naik kelas.
Ani rajin belajar.
Kesimpulan yang sah adalah …

1. Ani naik kelas.
2. Ani dapat hadiah.
3. Ani tidak dapat hadiah.
4. Ani naik kelas dan dapat hadiah.
5. Ani dapat hadiah atau naik kelas.

PEMBAHASAN :
Diketahui pernyataan:
p = Ani rajin belajar.
q = Ani naik kelas.
r = Ani dapat hadiah.
Dari pernyataan di atas diperoleh  premis-premis seperti di bawah ini: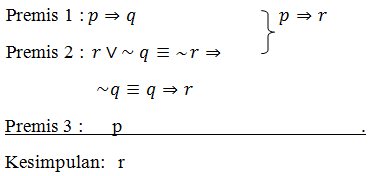

Maka, kesimpulan yang sah adalah Ani dapat hadiah.
Jawaban : B

Soal No.25 (Matematika Dasar SNMPTN 2011)

Jika ~ p adalah negasi dari P maka kesimpulan dari pernyataan-pernyataan:  ~ p ⇒ ~ q dan q ∨ ~ r adalah …

1. r ∧ q
2. p ∨ ~r
3. p ⇒ r
4. ~r ⇒ ~q
5. ~q ⇒ ~p

PEMBAHASAN :
Diketahui premis:
Premis 1 : ~p → ~q
Premis 2 : q ∨ ~r ≡ ~q → ~r
Kesimpulan : ~p → ~r ≡ p ∨ ~r
Jawaban : B

Soal No.26 (UN 2014)

Diketahui premis-premis berikut:
Premis 1 : Ada siswa yang tidak rajin belajar atau hasil ulangan baik.
Premis 2 : Jika hasil ulangan baik maka beberapa siswa dapat mengikuti seleksiperguruan tinggi.
Premis 3 : Semua siswa tidak dapat mengikuti seleksi perguruan tinggi.
Kesimpulan yang sah dari ketiga premis tersebut adalah…

1. Ada siswa yang hasil ulangan baik.
2. Ada siswa yang hasil ulangan tidak baik.
3. Ada siswa yang rajin belajar.
4. Ada siswa yang tidak rajin belajar.
5. Semua siswa rajin belajar.

PEMBAHASAN :
Diketahui pernyataan:
p = siswa tidak rajin belajar.
q = hasil ulangan baik.
r = siswa dapat mengikuti seleksi perguruan tinggi.
Dari pernyataan di atas diperoleh  premis-premis seperti di bawah ini:

Maka, kesimpulan yang sah dari ketiga premis di atas adalah ada siswa yang tidak  rajin belajar.
Jawaban : D

Soal No.27 (Matematika Dasar SNMPTN 2011)

Jika ~ p adalah negasi dari P maka kesimpulan dari pernyataan-pernyataan:  p ⇒ ~ q dan q ∨ ~ r adalah …

1. r ∨ p
2. r ∧ p
3. ~p ∨ ~r
4. r ∨ ~q
5. ~q ⇒ p

PEMBAHASAN :
Diketahui premis:
Premis 1 : p  ⇒ ~q
Premis 2 : q ∨ ~r ≡ ~q → ~r
Kesimpulan : p ⇒ ~r ≡ ~p ∨ ~r
Jawaban : C

Soal No.28 (UN 2010)

Perhatikan premis-premis berikut:
Premis 1 : Jika saya giat belajar maka saya akan meraih juara.
Premis 2 : Jika saya bisa meraih juara maka saya boleh ikut bertanding.
Ingkaran dari kesimpulan kedua premis tersebut adalah …

1. Saya giat belajar dan saya tidak boleh ikut bertanding.
2. Saya giat belajar atau saya tidak boleh ikut bertanding.
3. Saya giat belajar maka saya bisa meraih juara.
4. Saya giat belajar dan saya boleh ikut bertanding.
5. Saya ikut bertanding maka saya giat belajar.

PEMBAHASAN :
Diketahui pernyataan:
p = saya giat belajar.
q = saya bisa meraih juara.
r = saya boleh ikut bertanding.
Dari pernyataan di atas diperoleh  premis-premis seperti di bawah ini:
Premis 1 : p ⇒ q
Premis 2 : q ⇒ r
Kesimpulan : p ⇒ r
~(p ⇒ r) = ~(~p ∨ r) = p ∧ ~r
Maka, ingkaran dari kesimpulan kedua premis di atas  adalah saya giat belajar dan saya tidak boleh ikut bertanding.
Jawaban : A

Soal No.29 (Matematika IPA UM UGM 2010)

Diberikan pernyataan a, b, c, d dan ~a menyatakan ingkaran a. Jika pernyataan-pernyataan berikut benar: a ⇒ (b ∨ d), b ⇒ c, (b ∨ c) ⇒ d dan d pernyataan yang salah adalah …

1. ~a
2. ~b
3. ~a ∨ b
4. a ∨ ~c
5. b ∧ c

PEMBAHASAN :
Diketahui:

• Pernyataan a, b, c, d
• ~ a ingkaran a
• a ⇒ (b ∨ d), b ⇒ c, dan (b ∨ c) ⇒ d adalah pernyataan benar
• d adalah pernyataan yang salah

1. a ⇒ (b ∨ d) bernilai benar, a ⇒ salah atau salah ≡ bernilai benar sehingga a harus bernilai salah
2. b ⇒ c bernilai benar.
3. (b ∨ c) ⇒ d bernilai benar karena d bernilai salah maka (b ∨ c) harus bernilai salah sehingga b bernilai salah dan c juga bernilai salah.

Jawaban : E

Soal No.30 (UN 2010)

Diberikan premis-premis sebagai berikut:
Premis 1 : Jika harga BBM naik, maka harga bahan pokok naik.
Premis 2 : Jika harga bahan pokok naik, maka semua orang tidak senang.
Ingkaran dari kesimpulan tersebut adalah …

1. Harga BBM tidak naik.
2. Jika harga bahan pokok naik maka ada orang yang tidak senang.
3. Harga bahan pokok naik atau ada orang tidak senang.
4. Jika semua orang tidak senang maka harga bahan pokok naik.
5. Harga BBM naik dan ada orang yang senang.

PEMBAHASAN :
Diketahui pernyataan:
p = Harga BBM naik.
q = Harga bahan pokok naik.
r = Semua orang tidak senang.
Dari pernyataan di atas diperoleh  premis-premis seperti di bawah ini:
Premis 1 : p ⇒ q
Premis 2 : q ⇒ r
Kesimpulan : p ⇒ r
~(p ⇒ r) = ~(~p ∨ r) = p ∧ ~r
Maka, ingkaran dari kesimpulannya adalah harga BBM naik dan ada orang yang senang.
Jawaban : E