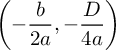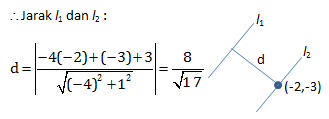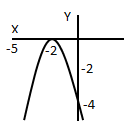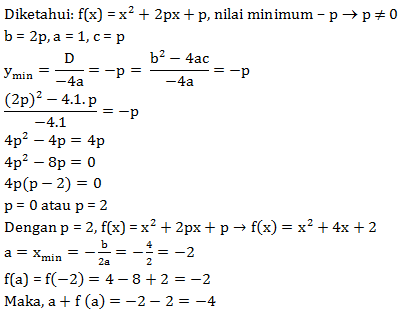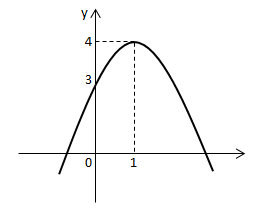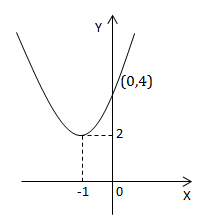Untuk Pembelajaran selanjutnya…
Fungsi Kuadrat
Fungsi kuadrat juga dikenal sebagai fungsi polinom atau fungsi suku banyak berderajat dua dalam variabel x.
Bentuk Umum
Bentuk umum fungsi kuadrat: ƒ(x) = ɑx2 + bx + c , (a, b, dan c ∈ R, ɑ ≠ 0) untuk semua nilai x dalam daerah asalnya. Grafik fungsi kuadrat dalam bidang Cartesius dikenal sebagai parabola.
- Koordinat titik puncak atau titik balik
ƒ(x) = y = ɑx2 + bx + c , (a, b, dan c ∈ R, ɑ ≠ 0) mempunyai titik puncak atau titik balik


- Sumbu simetri x = xp
- Nilai maksimum/minimum y = yp
Sifat Kurva Parabola
- Berdasarkan koefisien “ɑ”
Nilai a berfungsi untuk menentukan arah membukanya sebuah grafik.- Jika a > 0, parabola terbuka ke atas sedangkan titik baliknya minimum sehingga mempunyai nilai minimum.
- Jika a < 0, parabola terbuka ke bawah sedangkan titik baliknya maksimum sehingga mempunyai nilai maksimum.
- Berdasarkan koefisien “b”
Nilai b berfungsi untuk menentukan posisi sumbu simetri pada grafik.- Untuk a dan b bertanda sama (a > 0, b > 0) atau (a < 0, b <0) maka, sumbu simetri berada di kiri sumbu y.
- Untuk a dan b berlainan tanda (a < 0, b > 0) atau (a > 0, b < 0) maka, sumbu simetri berada di kanan sumbu y.
- Berdasarkan koefisien “c”
Nilai c berfungsi untuk menentukan titik potong dengan sumbu y.- Jika c > 0, grafik parabola memotong di sumbu y positif.
- Jika c < 0, grafik parabola memotong di sumbu y negatif.
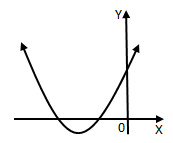
- Berdasarkan D = b2 – 4ac (diskriminan)
- Jika D > 0 persamaan kuadrat mempunyai dua akar real yang berlainan. Parabola akan memotong sumbu x di dua titik. Untuk D kuadrat sempurna maka kedua akarnya rasional, sedangkan D tidak berbentuk kuadrat sempurna maka kedua akarnya irasional.
- Jika D = 0 persamaan kuadrat mempunyai dua akar yang sama (akar kembar), real, dan rasional. Parabola akan menyinggung di sumbu x.
- Jika D < 0 persamaan kuadrat tidak mempunyai akar real atau kedua akarnya tidak real (imajiner). Parabola tidak memotong dan tidak menyinggung di sumbu x.
- Untuk D < 0, a > 0 parabola akan selalu berada di atas sumbu x atau disebut definit positif.
- Untuk D < 0, ɑ < 0 parabola akan selalu berada di bawah sumbu x atau disebut definit negatif.
Menyusun Fungsi kuadrat
- Apabila memotong di sumbu x di (x1,0) dan (x2,0), maka rumus yang berlaku: y = ƒ (x) = ɑ (x – x1) (x – x2).
- Apabila titik puncak (xp, yp) maka rumus yang berlaku: y = ƒ (x) = ɑ (x – xp)2 + yp.
- Apabila menyinggung sumbu x di (x1,0) maka rumus yang berlaku: y = ƒ (x) = ɑ (x – x1)2.
Hubungan Garis Dengan Parabola
Berdasarkan D = b2 – 4ac, kedudukan garis terhadap parabola dibagi menjadi 3, yaitu:
- D > 0 artinya garis akan memotong parabola di dua titik.
- D = 0 artinya garis memotong parabola di satu titik (menyinggung)
- D < 0 artinya garis tidak memotong dan tidak menyinggung parabola.
Soal No.1 (UTBK 2019)
Misalkan l1 menyatakan garis singgung kurva y = x2 + 1 di titik (2,5) dan I2 menyatakan garis singgung kurva y = 1 – x2 yang sejajar dengan garis l1. Jarak l1 dan l2 adalah….
PEMBAHASAN :
Garis singgung 1, di (2,5) :
- Gradien l1 : m1 = y1‘ = (x2 + 1)’ = 2x = 2.(2) = 4
- l1 : y – 5 = 4(x-2)
⇒ y = 4x – 3
⇒ -4x + y + 3 = 0
Garis singgung 2
- Gradien l2 : m2 = m1 (karena l1 // l2)
⇒ m2 = 4
⇒ (1 – x2 = 4
⇒ -2x = 4
⇒ x = -2, y = 1 – (-2)2 = -3
Soal No.2 (SBMPTN 2018)
Jika garis singgung kurva y = 3x2 di titik P(a,b) dengan a ≠ 0 memotong sumbu x di titik Q(4,0), maka a+b adalah….
- 21/4
- 33/4
- 52
- 184
- 200
PEMBAHASAN :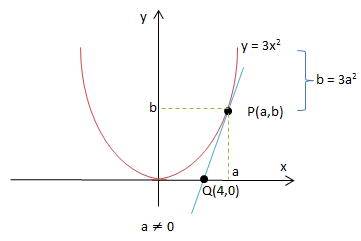
mpq = y’x = a
⇒ m = 6a![]()
⇒ 3a2 = 6a2-24a
⇒ 0 = 3a2-24a
⇒ 0 = 3a-24
⇒ 8 = a
b = 3.(8)2 = 192
∴ a+b = 8+192 = 200
Jawaban E
Soal No.3 (MADAS SNMPTN 2012)
Jika gambar di bawah ini adalah grafik fungsi kuadrat f dengan titik puncak (-2,0) dan melalui titik (0,-4) maka nilai f(-5) adalah …
- -7
- -8
- -9
- -10
- -11
PEMBAHASAN :
Diketahui titik puncak ( xp , yp) = (-2,0), melalui titik (x , y) = (0,-4)
Rumus yang sesuai apabila diketahui titik puncak:
y = f(x) = a(x-xp )2 + yp
Untuk mencari nilai a:
y = f(x) = a(x-xp)2 + yp
y = a(x+2)2 + 0
-4 = a(0+2)2 + 0
-4 = 4a
a = -1
Sehingga
f(x) = -(x + 2)2, dengan f(-5)
f(-5) = -(-5 + 2)2 = -9
Jawaban : C
Soal No.4 (UN 2010)
Absis titik balik grafik fungsi y = px2 + (p – 3)x + 2 adalah p. Nilai p = …
- -3
- -3/2
- -1
- 2/3
- 3
PEMBAHASAN :
Diketahui:
y = px2 + (p – 3)x + 2
xp = p
Ditanyakan: nilai p = …
Untuk menentukan absis titik puncak = xp = – b/2a![]()
-p + 3 = 2p2
2p2 + p – 3 = 0
(2p + 3)(p – 1) = 0
p = – 3/2 atau p = 1
Maka, nilai p yang sesuai adalah p = – 3/2
Jawaban : B
Soal No.5 (MatDas SBMPTN 2013)
Jika grafik fungsi kuadrat f(x) = ax2 + bx + c mempunyai titik puncak (8,4) dan memotong sumbu-x negatif maka …
- a > 0, b > 0 dan c > 0
- a < 0, b < 0 dan c > 0
- a < 0, b > 0 dan c < 0
- a > 0, b > 0 dan c < 0
- a < 0, b > 0 dan c > 0
PEMBAHASAN :
Diketahui titik puncak (8,4)
maka grafik terbuka ke bawah, maka a < 0
xp = -b/2a = 8, karena a < 0 → b > 0
D = b2 – 4ac, syarat memotong sumbu x negatif D > 0
karena b > 0 dan a < 0, maka:
b2 – 4ac > 0
(+) – 4(-)c > 0
c > 0
Jawaban : E
Soal No.6 (UN 1998)
Diketahui fungsi kuadrat f(x) = – 2x2 + 4x + 3 dengan daerah asal {x|-2 ≤ x ≤ 3, x ∈ R}. Daerah hasil fungsi adalah …
- {y|-3 ≤ y ≤ 5, x ∈ R}
- {y|-3 ≤ y ≤ 3, x ∈ R}
- {y|-13 ≤ y ≤ -3, x ∈ R}
- {y|-13 ≤ y ≤ 3, x ∈ R}
- {y|-13 ≤ y ≤ 5, x ∈ R}
PEMBAHASAN :
Diketahui: {x|-2 ≤ x ≤ 3, x ∈ R}
x = -2, x = 1, x = 3
f(x) = -2x2 + 4x + 3
xp = -b/2a = -4/(2.-2) = 1
Untuk x = -2 → f (-2) = – 2(- 2)2 + 4 (- 2) + 3 = – 8 – 8 + 3 = – 13
Untuk x = 1 → f(1)= -2(1)2 + 4(1) + 3 = -2 + 4 + 3 = 5
Untuk x = 3 → 3 f(3) = -2(3)2 + 4(3) + 3 = -18 + 12 + 3 = – 3
Maka, {y|-13 ≤ y ≤ 5, x ∈ R}
Jawaban : E
Soal No.7 (Matematika IPA SBMPTN 2014)
Diketahui suatu parabola simetris terhadap garis x = -2 dan garis singgung parabola tersebut dititik (0,1) sejajar dengan garis 4x + y = 4 . Titik puncak parabola tersebut adalah …
- (-2,-3)
- (-2,-2)
- (-2,0)
- (-2,1)
- (-2,5)
PEMBAHASAN :
Diketahui:
Asumsikan persamaan parabola y = ax2 + bx + c
parabola simetris terhadap garis xp = -2
Tentukan xp = -b/2a =-2 → b = 4
garis ≡ 4x+y = 4 → mg = -4
karena sejajar maka mparabola = mgaris = -4
mparabola = y
2ax + b = -4 melalui titik (0,1)
2a(0) + b = -4
b = -4
Untuk menentukan xp dan yp:
b = 4a
-4 = 4a
a = -1
persamaan parabola y = ax2 + bx + c
y = -x2 – 4x + c melalui titik (0,1)
1 = -02 – 4(0) + c
c = 1
Maka dapat dihitung y = -x2 – 4x + 1
xp = -b/2a = -(-4)/2(-1) = -2 dan yp = -(-2)2 – 4(-2) +1= 5
Titik puncak parabola adalah (-2,5)
Jawaban : E
Soal No.8 (UN 2008)
Persamaan grafik fungsi kuadrat yang melalui titik A(1,0), B(3,0), dan C(0,-6) adalah …
- y = 2x2 + 8x – 6
- y = -2x2 + 8x – 6
- y = 2x2 – 8x + 6
- y = -2x2 – 8x – 6
- y = -x2 + 4x – 6
PEMBAHASAN :
Untuk titik C (0,-6) → x = 0, y = – 6
Untuk titik A (1,0) dan B (3,0) → x1 = 1, x2 = 3
Maka rumus yang berlaku y = a(x – x1)(x – x2)
y = a(x – 1)(x – 3)
– 6 = (0 – 1)(0 – 3)
– 6 = 3a
a = – 2
Menentukan fungsi kuadrat:
y = a(x – x1)(x – x2)
y = – 2(x – 1)(x – 3)
y = – 2(x2 – 4x + 3)
y = – 2x2 + 8x – 6
Jawaban : B
Soal No.9 (TKPA SBMPTN 2014)
Fungsi kuadrat f(x) = x2 + 2px + p mempunyai nilai minimum –p dengan p ≠ 0. Jika sumbu simetri kurva f adalah x = a, maka nilai a + f(a) = …
- 6
- 4
- -4
- -5
- -6
Soal No.10 (UN 2007)
Perhatikan gambar!
Persamaan grafik fungsi kuadrat pada gambar adalah …
- y = -2x2 + 4x + 3
- y = -2x2 + 4x + 2
- y = -x2 + 2x + 3
- y = -2x2 + 4x – 6
- y = -x2 + 2x – 5
PEMBAHASAN :
Diketahui:
(xp , yp) = (1,4)
(x , y) = (0,3)
Ditanyakan: Fungsi kuadrat yang terbentuk
Untuk parabola yang memiliki titik puncak rumus yang berlaku sebagai berikut:
y = a(x – xp)2 + yp
y = a (x – 1)2 + 4
3 = a(0 -1)2 + 4
3 = a + 4
a = -1
Fungsi kuadrat yang terbentuk adalah
y = a(x – xp)2 + yp
y = -1(x -1)2 + 4
y = -x2 + 2x + 3
Jawaban : C
Soal No.11 (MatDas SNMPTN 2009)
Grafik fungsi f(x)=x2 – 6x + 7 dapat diperoleh dengan cara menggeser grafik fungsi f(x) = x2 ke arah …
- Kanan sumbu x sejauh 2 satuan dan ke arah bawah sumbu y sejauh 3 satuan
- Kiri sumbu x sejauh 3 satuan dan ke arah atas sumbu y sejauh 2 satuan
- Kanan sumbu x sejauh 3 satuan dan ke arah atas sumbu y sejauh 2 satuan
- Kanan sumbu x sejauh 6 satuan dan ke arah atas sumbu y sejauh 7 satuan
- Kiri sumbu x sejauh 2 satuan dan ke arah atas sumbu y sejauh 3 satuan
PEMBAHASAN :
Diketahui: f(x) = x2 – 6x + 7
Ditanyakan: f(x) = x2 digeser ke arah?
f(x) = x2 – 6x + 7 = (x – 3)2 – 2
Maka, grafik fungsi f(x) digeser ke arah anan sumbu x sejauh 3 satuan dan ke arah atas sumbu y sejauh 2 satuan.
Jawaban : C
Soal No.12 (UN 2007)
Perhatikan gambar!
Persamaan grafik fungsi pada gambar adalah …
- y = 2x2 + 4
- y = x2 + 3x + 4
- y = 2x2 + 4x + 4
- y = 2x2 + 2x + 4
- y = x2 + 5x + 4
PEMBAHASAN :
Diketahui:
(xp , yp) = (-1,2)
(x , y) = (0,4)
Ditanyakan: Persamaan kuadratnya = …
Rumus yang berlaku:
y = a(x – xp)2 + yp
y = a (x – (- 1))2 + 2
4 = a(0 +1)2 + 2
4 = a + 2
a = 2
Persamaan kuadrat yang terbentuk adalah
y = a(x – xp)2 + yp
y = 2(x + 1)2 + 2
y = 2x2 + 4x + 4
Jawaban : C
Soal No.13 (Matematika Dasar SNMPTN 2011)
Grafik fungsi y = ax2 + bx + c di tunjukkan berikut ini:
- ab > 0 dan a + b + c > 0
- ab < 0 dan a + b + c > 0
- ab > 0 dan a + b + c ≤ 0
- ab < 0 dan a + b + c < 0
- ab < 0 dan a + b + c ≥ 0
PEMBAHASAN :
Diketahui:
Kurva terbuka ke atas → a > 0
y = ax2 + bx + c memotong sumbu y positif → c > 0
Kurva memotong sumbu x di dua titik → D > 0
Maka: b2 – 4ac > 0
b2 – 4(+)(+) > 0
b > 0
Sehingga, ab > 0 dan a + b + c > 0
Jawaban : A
Soal No.14 (UN 1995)
Suatu fungsi kuadrat f(x) mempunyai nilai maksimum 5 untuk x = 2, sedangkan f(4) = 3. Fungsi kuadrat tersebut adalah …
- y = – ½ x2 + 2x + 3
- y = – ½ x2 – 2x + 3
- y = – ½x2 – 2x – 3
- y = – 2x2 – 2x + 3
- y = – 2x2 + 8x – 3
PEMBAHASAN :
Diketahui:
(xp , yp) = (2,5)
f(4) = 3 → (4,3)
Tentukan nilai a:
y = a(x – xp)2 + yp
y = a(x – 2)2 + 5
3 = a (4 – 2)2 + 5
3 = 4a + 5
4a = – 2
a = – ½
Maka, fungsi kuadratnya menjadi sebagai berikut:
y = – ½ (x-2)2 + 5
y = – ½ x2 + 2x + 3
Jawaban : A
Soal No.15 (MATEMATIKA DASAR SNMPTN 2011)
Jika grafik fungsi kuadrat f(x) = ax2 + bx + c dengan titik puncak (5,-4) memotong sumbu x positif dan sumbu y negatif maka …
- a – c > 0
- a + c < 0
- a + c = 0
- a + c > 0
- a – c < 0
PEMBAHASAN :
Diketahui:
f(x) = ax2 + bx + c
Kordinat titik puncak (5,4)
Memotong pada sumbu y negatif →
Tentukan xp dan yp: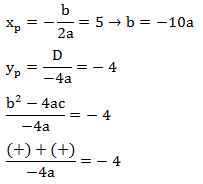
a > 0
Maka, a – c > 0
Jawaban : C
Soal No.16 (UN 2003)
Grafik fungsi kuadrat dengan titik balik (-1,4) dan melalui titik (-2,3) memotong sumbu y di titik …
- (0,3)
- (0, 2½)
- (0,2)
- (0, 1½)
- (0,1)
PEMBAHASAN :
Diketahui:
titik balik (xp , yp) → (-1,4)
(x , y) → (-2,3)
Tentukan terlebih dahulu fungsi kuadratnya:
y = a(x-xp)2 + yp
y = a(x+1)2 + 4
3 = a(-2+1)2 + 4
3 = a + 4
a = -1
Fungsi kuadrat yang memenuhi adalah:
y = -1(x+1)2 + 4
Maka, titik potong dengan sumbu y ⟶ x = 0
y = -1(0+1)2 + 4 = 3
(0 , 3)
Jawaban : A
Soal No.17 (Matematika Dasar Simak UI 2012)
Diketahui bahwa f(x) adalah fungsi kuadrat yang memenuhi pertidaksamaan x^2-2x + 3 ≤ f(x) ≤ 2x2 – 4x + 4 untuk semua bilangan riil x. Jika diketahui bahwa f(5) = 26, maka f(7) = …
- 38
- 50
- 56
- 74
- 92
PEMBAHASAN :
Diketahui: x2 – 2x + 3 ≤ f(x) ≤ 2x2 – 4x + 4, x merupakan bilangan riil, f(5) = 26
Ditanyakan: Fungsi kuadrat untuk f(7)?
Untuk f(5) = 26:
x2 – 2x + 3 ≤ f(x) ≤ 2x2 – 4x + 4
52 – 2(5) + 3 ≤ f(5) ≤ 2(5) – 4(5) + 4
18 ≤ f(5) ≤ 34
18 ≤ 26 ≤ 34
Untuk f(7):
x2 – 2x + 3 ≤ f(x) ≤ 2x2 – 4x + 4
72 – 2(7) + 3 ≤ f(7) ≤ 2(7)2 – 4(7) + 4
38 ≤ f(7) ≤ 74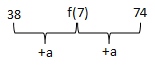
38 + 2a = 74
a = 18
Maka, f(7) = 38 + 18 = 56
Jawaban : C
Soal No.18 (UN 2008)
Pak bahar mempunyai sebidang tanah berbentuk persegi panjang dengan lebar 10 m kurangnya dari setengah panjangnya. Apabila luasnya 400 m2 maka lebarnya adalah … meter
- 60
- 50
- 40
- 20
- 10
PEMBAHASAN :
Diketahui: L = 400 m2, l = ½p – 10
Tentukan panjang tanah terlebih dahulu:
l = ½p – 10 ⟶ p = 2l + 20
l = p.l = (2l + 20) . l
400 = 2l2 + 20l
2l2 + 20l – 400 = 0
l2 + 10l – 200 = 0
(l – 10)(l + 20)
l = 10 atau l = -20
Maka lebar tanah adalah 10
Jawaban : E
Soal No.19 (MATEMATIKA DASAR SIMAK UI 2012)
Diketahui f(x) = ax2 + (b + 1)x – (a + b + 1) memotong sumbu x di dua titik berbeda. f(x) dibagi x mempunyai sisa – (a+6), maka a dipenuhi oleh …
- a < -3 atau a > 3
- -3 < a < 3
- a ≠ -6
- a < -2 atau a > 8
- -2 < a < 8
PEMBAHASAN :
Diketahui:
f(x) = ax2 + (b + 1)x – (a + b + 1) memotong sumbu x di dua titik berbeda → D > 0
f(x) dibagi x mempunyai sisa – (a+6)
Ditanyakan nilai a?
D = b2 – 4ac
b = (b + 1), a = a, c = – (a + b + 1)
Persamaan 1: (b + 1)2 – 4.a.(-(a + b + 1)) > 0
Persamaan 2: f(x) dibagi x mempunyai sisa –(a + 6) → f(0) = -(a + 6)
-(a + b + 1) = -(a + 6)
a + b + 1 = a + 6
a + b + 1 = 6 → b = 5 – a
Subtitusikan persamaan 1 dan 2:
(5 – a + 1 – 4a(- a + 5 – a + 1) > 0
(5 – a + 1 – 4a(-6) > 0
(6 – a)2 + 24a > 0
a2 – 12a + 36 + 24a > 0
a2 + 12a + 36 > 0
(a + 6)(a + 6) > 0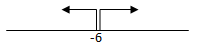
Maka, a ≠ -6
Jawaban : C
Soal No.20 (UN 2011)
Grafik y = px2 + (p + 2)x – p + 4 memotong sumbu x di dua titik. Batas – batas nilai p yang memenuhi adalah …
- p < -2 atau p > -2/5
- p < 2/5 atau p > 2
- p < 2 atau p > 10
- 2/5 < p < 2
- 2 < p < 10
PEMBAHASAN :
Diketahui dari grafik y = px2 + (p + 2)x – p + 4, yaitu:
b = p + 2
a = p
c = – p + 4
D = b2 – 4ac, syarat memotong sumbu x di dua titik D > 0
b2 – 4ac > 0
(p+2)2 – 4.p.(-p + 4) > 0
p2 – 4p + 4 + 4p2 – 16p > 0
5p2 – 12p + 4 > 0
(5p – 2)(p – 2) > 0
p = 2/5 atau p = 2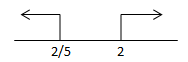
Sehingga, p < 2/5 atau p > 2
Jawaban : B
Soal No.21 (TKPA SBMPTN 2014)
Untuk 0 < a < 10, fungsi kuadrat f(x) = ax2 + 2ax + 10 memenuhi sifat …
- Selalu negatif
- Selalu positif
- Hanya positif pada setiap x, dengan 0 < x < 10
- Hanya negatif pada setiap x, dengan 0 < x < 10
- Hanya positif pada setiap x, dengan x < 0 atau x > 10
PEMBAHASAN :
Diketahui:
0 < a < 10
f(x) = ax2 + 2ax + 10, b = 2a, a = a, c = 10
Ditanyakan: Sifat yang memenuhi fungsi kuadrat?
0 < a < 10 → a > 0
D = b2 – 4ac
D = (2a)2 – 4.a.10 = 4a2 – 40a < 0
Untuk a > 0, D < 0 maka definit positif (selalu positif untuk setiap x)
Jawaban : B
Soal No.22 (UN 2011)
Grafik fungsi kuadrat f(x) = ax2 + 2√2x + (a-1), a≠0 memotong sumbu x di dua titik berbeda. Batas – batas nilai a yang memenuhi adalah …
- a < -1 atau a > 2
- a < -2 atau a > 1
- -1 < a < 2
- -2 < a < 1
- -2 < a < -1
PEMBAHASAN :
Diketahui: grafik f(x) = ax2 + 2√2x + (a-1), a≠0
b = 2√2
a = a
c = a – 1
D = b2 – 4ac, syarat memotong sumbu x di dua titik D
(2√2)2 – 4a(a-1) > 0
8 – 4a2 + 4a > 0
4a2 – 4a – 8 < 0
a2 – a – 2 < 0
(a – 2)(a + 1) < 0
a = 2 atau a = 1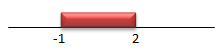
Sehingga, -1 < a < 2
Jawaban : C
Soal No.23 (Matematika IPA SNMPTN 2007)
Parabola y = ax2 – (a+2)x + 9/4 memotong sumbu x di dua titik berbeda (x1, 0) dan (x2, 0). Jika x1+x2 dan x1 x2 masing-masing merupakan suku pertama dan rasio suatu barisan geometri, dan jumlah suku pertama dan rasio tersebut adalah 45/4a maka ekstrem parabola tersebut berupa …
- Minimum di titik x = 5/14
- Maksimum di titik x = – 9/7
- Minimum di titik x = 9/7
- Maksimum di titik x = – 9/14
- Minimum di titik x = 9/14
Soal No.24 (UN 2010)
Grafik fungsi kuadrat f(x) = x2 + bx + 4 menyinggung garis y = 3x + 4. Nilai b yang memenuhi adalah …
PEMBAHASAN :
Diketahui:
f(x) = x2 + bx + 4
y = 3x + 4
Sedangkan f(x) = y
x2 + bx + 4 = 3x + 4
x2 + (b-3)x = 0
Maka:
b = b – 3
a = 1
c = 0
D = b2 – 4ac syarat menyinggung adalah D = 0
b2 – 4ac = 0
(b-3)2 – 4.1.0 = 0
(b-3)2 = 0
b = 3
Sehingga, nilai b = 3
Jawaban : D
Soal No.25 (Matematika Dasar UM UGM 2013)
Parabola y = -x2 + 2ax + a-1 dan garis y = ax + a – 2 berpotongan di (x1, y1) dan (x2, y2) Jika x1 + x2 = 2 dan y1 + y2 =..
- 1
- 2
- 3
- 4
PEMBAHASAN :
Diketahui:
Parabola y = -x2 + 2ax + a – 1
Garis y = ax + a – 2
Titik potong di (x1, y1) dan (x2, y2)
x1 + x2 = 2
Ditanyakan: y1+ y2 ?
y = y, parabola berpotongan dengan garis
ax + a-2 = -x2 + 2ax + a – 1
x2 – ax – 1 = 0
x1 + x2 = 2 → a = 2
Untuk mencari nilai x dari persamaan ∶ x2 – 2x – 1 = 0
(x – 2)(x + 1) = 0
x = 2 atau x = -1
Untuk a = 2 diperoleh
y = ax + a – 2
y = 2x + 2 – 2
y = 2x
Sehingga :
untuk x = 2 → y1 = 4
untuk x = -1 → y2 = -2
Maka, y1+ y2 = 4 + (-2) = 2
Jawaban : C
Soal No.26 (UN 2010)
Agar garis y = -2x + 3 menyinggung parabola y = x2 + (m-1)x + 7 maka nilai m yang memenuhi adalah ….
- -5 atau -3
- -5 atau 3
- -3 atau 5
- -1 atau 17
- 1 atau 17
PEMBAHASAN :
Diketahui:
garis y = -2x + 3
parabola y = x2 + (m-1)x + 7
y = y
x2 + (m-1)x + 7 = -2x + 3
x2 + (m+1)x + 4 = 0
b = m + 1
a = 1
c = 4
D = b2 – 4ac, syarat menyinggung D = 0
b2 – 4ac = 0
(m+1)2 – 4.1.4 = 0
m2 + 2m + 1 – 16 = 0
m2 + 2m – 15 = 0
(m+5)(m-3)=0
Maka nilai m yang memenuhi adalah
m = -5 atau m = 3
Jawaban : B
Soal No.27 (Matematika Dasar Simak UI 2009)
Diberikan fungsi f(x) = ax2 + bx + c. jika grafik fungsi tersebut melalui titik (2,21) dan mempunyai garis singgung yang sejajar dengan sumbu x pada (-2,-11), maka nilai a + b + c adalah …
- 4
- 5
- 6
- 7
- 8
PEMBAHASAN :
Diketahui: fungsi f(x) = ax2 + bx + c , melalui titik (x, y) ® (2,21)
Persamaan 1:
f(x) = y = ax2 + bx + c
21 = a(2)2 + b(2) + c
21 = 4a + 2b+c
Persamaan 2:
Sedangkan untuk garis yang sejajar sumbu x maka m = 0, melalui titik (x , y) ® (-2,-11)
m = y = 2ax + b
0 = -4a + b
b = 4a
Persamaan 3:
f(x) = ax2 + bx + c melalui titik (x, y) ® (-2,-11)
-11 = a(-2)2 + b(-2) + c
-11 = 4a – 2b + c
Kemudian substitusikan (2) ke (1) dan ke (3)
Persamaan 1 : 21 = 4a + 2b + c
Persamaan 2: b = 4a
Persamaan 3: -11 = 4a – 2b + c
4a + 2(4a) + c = 21 → 12a + c = 21 …… persamaan 4
4a – 2(4a) + c = -11 → -4a + c = -11 …… persamaan 5
Kurangkan persamaan 4 dan 5:
12a + c = 21
-4a + c = -11
16a = 32
a = 2
b = 4a
b = 4.2 = 8
12a + c = 21
12.2 + c = 21
c = – 3
Maka, a + b + c = 2 + 8 – 3 = 7
Jawaban : D
Soal No.28 (UN 2013)
Grafik fungsi f(x) = mx2 + (2m-3)x + m + 3 berada di atas sumbu x. Batas – batas nilai m yang memenuhi adalah …
- m > 0
- m > 3/8
- m < 0
- 0 < m < 3/8
- – 3/8 < m < 0
PEMBAHASAN :
Diketahui: Grafik fungsi f(x) = mx2 + (2m-3)x + m + 3
b = 2m – 3
a = m
c = m + 3
D = b2 – 4ac, syarat berada di atas sumbu x (definit positif) a > 0, D < 0
a > 0, m > 0
D < 0
b2 – 4ac < 0
(2m – 3)2 – 4.m.(m + 3) < 0
4m2– 12m + 9 – 4m2-12m < 0
-24m < -9
m > 3/8
Sehingga, m > 3/8
Jawaban : B
Soal No.29 (Matematika Dasar SNMPTN 2007)
Agar garis y = -10x + 4 menyinggung parabola y = px2 + 2x – 2 maka konstanta p = …
- -2
- -3
- -4
- -5
- -6
PEMBAHASAN :
Diketahui:
garis y = -10x + 4
parabola y = px2 + 2x – 2
Ditanyakan: nilai p?
y = y
px2 + 2x – 2 = -10x + 4
px2 + 12x – 6 = 0 b = 12, a = p, c = – 6
D = b2 – 4ac, syarat menyinggung adalah D = 0
b2 – 4ac = 0
122 – 4.p.(– 6) = 0
144 – 4.p.(-6) = 0
144 + 24p = 0
p = -6
Jawaban : E
Soal No.30 (UN 2013)
Agar fungsi f(x) = (m + 3)x2 + 2mx + (m+1) definit positif, batas-batas nilai m yang memenuhi adalah ….
- m > -3
- m > -3/2
- m < 3
- m < -3/4
- -3 < m < -3/4
PEMBAHASAN :
Diketahui: fungsi f(x) = (m + 3)x2 + 2mx + (m+1)
b = 2m
a = m + 3
c = m + 1
D = b2 – 4ac, Syarat definit positif : a > 0, D < 0)
- D < 0
b2 – 4ac < 0
(2m)2 – 4.(m + 3).(m+1) < 0
4m2 – 4(m2+ 4m + 3) < 0
4m2 – 4m2 – 16m – 12 < 0
m < -3/4
Soal No.31 (Matematika IPA SBMPTN 2009)
Diberikan fungsi f memenuhi persamaan 3f(-x) + f(x-3) = x + 3 untuk setiap bilangan real x. Nilai 8f(-3) adalah …
- 24
- 21
- 20
- 16
- 15
PEMBAHASAN :
Diketahui: 3f(-x) + f(x-3) = x + 3, x = bilangan real
Ditanyakan: Nilai 8f(-3)?
3f(-x) + f(x – 3) = x + 3
Persamaan 1:
Untuk x = 0 → 3f(0) + f(-3) = 3
Persamaan 2:
Untuk x = 3 → 3f(-3) + f(0) = 6
Eliminasikan persamaan 1 dan 2:
3f(0) + f(-3) = 3 |x1| 3f(0) + f(-3) = 3
f(0) + 3f(-3) = 6 |x3| 3f(0) + 9f(-3) = 18
-8f(-3) = -15
8f(-3) = 15
Jawaban : E
Soal No.32 (UN 2013)
Nilai m yang menyebabkan fungsi kuadrat f(x) = (m+1)x2 – 2mx + (m – 3) definit negatif adalah …
- m < -3/2
- m < 1
- m > 3/2
- m > 1
- 1 < m < 3/2
PEMBAHASAN :
Diketahui: fungsi kuadrat f(x) = (m+1)x2 – 2mx + (m – 3)
b = 2m
a = m + 1
c = m – 3
D = b2 – 4ac, syarat definit negatif a < 0, D < 0
- a < 0, m + 1 < 0 ® m < -1
- D < 0
b2 – 4ac < 0(-2m)2 – 4.(m + 1).(m – 3) < 04m2 – 4 (m2 – 2m – 3) < 0
4m2– 4m2 + 8m + 12 < 0
8m < -12
m < -3/2
Nilai m yang memenuhi m < – 3/2
Jawaban : A
Semoga Bermanfaat