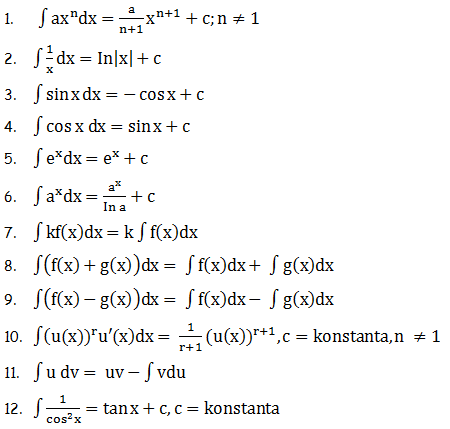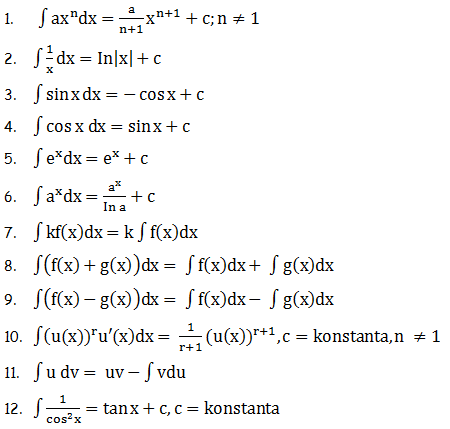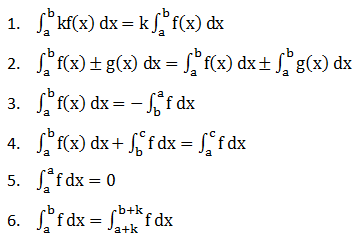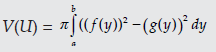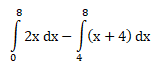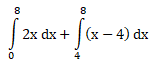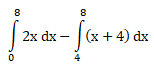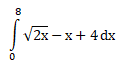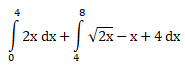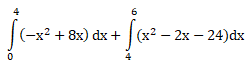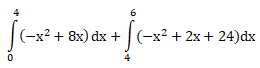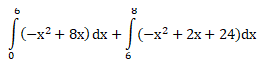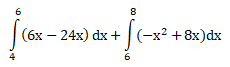Rangkuman, Contoh Soal Integral Pembahasan & Jawaban

By Posted on

Untuk Pembelajaran selanjutnya…

Pengertian

Integral merupakan kebalikan dari turunan. Jika F(x) adalah fungsi umum yang bersifat F(x) = f(x), maka F(x) merupakan anti turunan atau integral dari f(x). Pengintegralan fungsi f(x) terhadap x dinotasikan sebagai berikut.

∫ f(x) dx = F(x) + c

Keterangan:
∫ = notasi integral
f(x) = fungsi integran
F(x) = fungsi integral umum yang bersifat F(x) = f(x)
c = konstanta pengintegralan

Integral Tak Tentu

int17

Integral Tertentu

int18

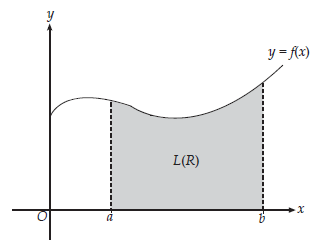
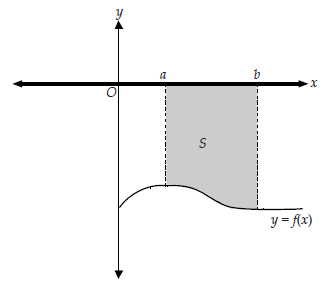
Menghitung Luas Daerah

Menentukan Luas Daerah diatas sumbu-x

int1

int2

Menentukan Luas Daerah di bawah sumbu-x

int3

int4

Menentukan Luas Daerah yang Terletak Dibatasi Kurva y = f(x) dan sumbu-x

int5

int6

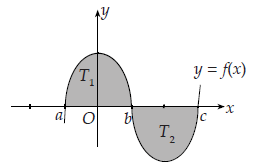
Menentukan Luas Daerah yang Terletak di Antara Dua Kurva

int7

int8

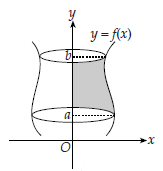
Menghitung Volume Benda Putar

Menentukan Volume Benda Putar yang Diputar Mengelilingi Sumbu-x

int9

int10

Menentukan Volume Benda Putar yang Diputar Mengelilingi Sumbu-y

int11

int12

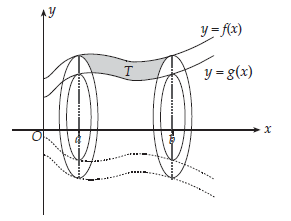
Menentukan Volume Benda Putar yang Dibatasi Kurva f(x) dan g(x) jika Diputar Mengelilingi Sumbu-x

int13

int14

Menentukan Volume Benda Putar yang Dibatasi Kurva f(y) dan g(y) Jika Diputar Mengelilingi Sumbu-y

int15

int16

Soal No.11

Tentukanlah integral x jika diketahui g1(x)’= x3

PEMBAHASAN :

Soal No.12

Tentukanlah integral x jika diketahui g1(x)’= 2x6 + 3

PEMBAHASAN :

Soal No.13

Tentukanlah integral x jika diketahui g1(x)’= x2 + 4x- 1/2

PEMBAHASAN :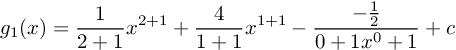


Soal No.14

Hitunglah integral dari

PEMBAHASAN :


Soal No.15

Hitunglah integral dari

PEMBAHASAN :
misal u = 9 – x2, maka du = -2x dx, x dx = du/-2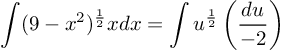



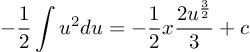
Soal No.16

Hitunglah integral dari

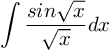
PEMBAHASAN :
misal





Soal No.17

Hitunglah integral dari

PEMBAHASAN :
misal u = 1-2x2, maka du = -4x dx





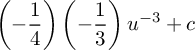
substitusikan u = 1-2x2 ke persamaan 12u-3 + c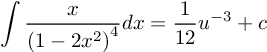

Soal No.18

Hitunglah integral berikut

PEMBAHASAN :
dengan mengubah
maka menjadi



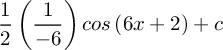
Soal No.19

Hitunglah integral berikut

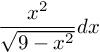
PEMBAHASAN :
jika dimisalkan x = 3 sin t, maka sin t = x/3 dan dx = 3 cos t dt.
jika dalam sebuah segitiga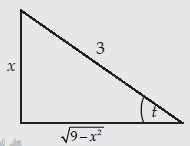
Untitled..




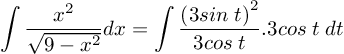
Dengan cos 2t = 1-2 sin2 t



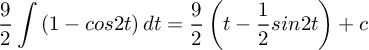
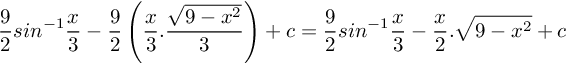
Soal No.20

Jika g'(x) = 2x-3 dan g(2) = 1, tentukanlah g(x).

PEMBAHASAN :

Untuk menentukan c dapat ditentukan dari g(2) = 1
g(x) = x2-3x+c
g(2) = 22-3.2 + c
1 = 4-6 + c
1 = -2 + c
c = 1 + 2
c = 3
maka, g(x) = x2 – 3x + 3

Soal No.21

Tentukan persamaan kurva yang melalui titik (-2,12) dan memiliki persamaan gradien garis singgung

PEMBAHASAN :



karena melalui titik (-2, 12), maka
f(-2) = 3(-2)2 – 15(-2) + c
12 = 3.4 + 30 + c
12 = 12 + 30 + c
12 = 42 + c
c = 12 – 42
c = -30
Maka persamaan kurvanya adalah f(x) = 3x2 – 15x – 30

Soal No.22

Hitunglah

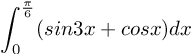
PEMBAHASAN :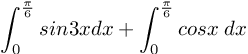



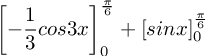
Soal No.23

Tentukan

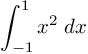
PEMBAHASAN :
karena merupakan fungsi genap, maka: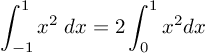

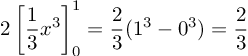
Soal No.24 (UN 2014)

Hasil

PEMBAHASAN :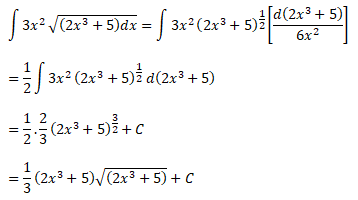

Jawaban : D

Soal No.25 (UN 2012)

Hasil dari

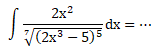
PEMBAHASAN :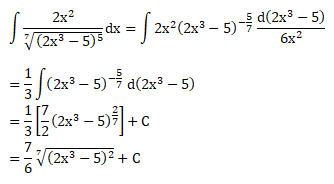

Jawaban : D

Soal No.26 (UN 2012)

Hasil

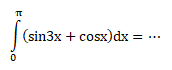
PEMBAHASAN :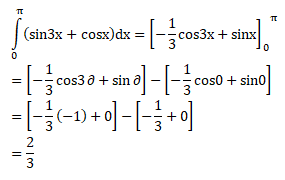

Jawaban : D

Soal No.27 (UN 2010)

Hasil dari
  1. -2 cos (x – 2π) + C
  2. -½ cos (x – 2π) + C
  3. ½ cos (x – 2π) + C
  4. cos (x – 2π) + C
  5. 2 cos (x – 2π) + C

PEMBAHASAN :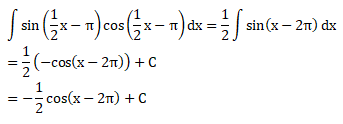

Jawaban : B

Soal No.28 (UN 2014)

Hasil
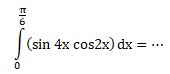
  1. 4/3
  2. 2/3
  3. 1/3
  4. 7/24
  5. -1/3

PEMBAHASAN :
Gunakan rumus trigonometri untuk menyelesaikan soal di atas, yaitu:
Trigonometri 2 sin A cos B = sin (A+B) +sin (A-B)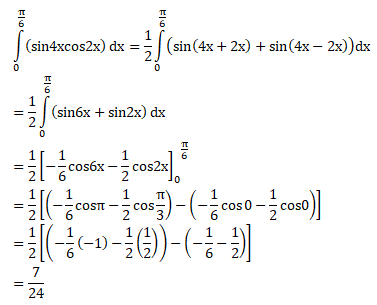

Jawaban : D

Soal No.29 (UN 2005)

Hasil dari

PEMBAHASAN :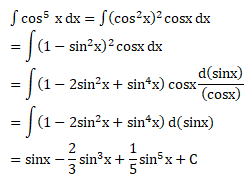

Jawaban : D

Soal No.30 (UN 2014)

Hasil dari

PEMBAHASAN :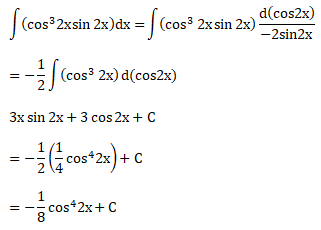

Jawaban : D

Soal No.31 (UN 2005)

Hasil dari

PEMBAHASAN :

Sehingga,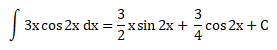

Jawaban : D

Soal No.32 (UN 2014)

Luas daerah yang diarsir pada gambar dapat dinyatakan dengan rumus …

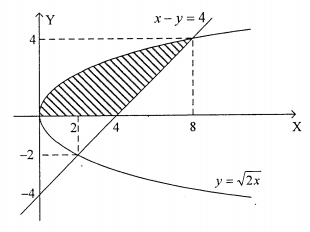
PEMBAHASAN :
Perhatikan grafik berikut:

Menentukan luas daerah berdasarkan gambar di atas: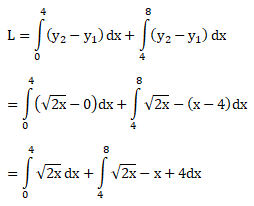

Jawaban : E

Soal No.33 (UN 2012)

Luas daerah yang dibatasi oleh kurva y = x2 + 3x + 4 dan y = 1 – x adalah …

  1. 2/3 satuan luas
  2. 4/3 satuan luas
  3. 7/4 satuan luas
  4. 8/3 satuan luas
  5. 15/3 satuan luas

PEMBAHASAN :
Persamaan untuk kurva yang terbentuk pada grafik adalah y = x2 + 3x + 4 dan y = 1 – x, maka:
⇒ y = y
⇒ x2 + 3x + 4 = 1 – x
⇒ x2 + 4x + 3 = 0
⇒ (x + 3) (x + 1)
x = – 3 dan x = – 1

Untuk menghitung luas daerah pada kurva yang terbentuk, sebagai berkut: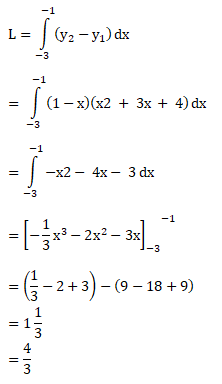

Jawaban : B

Soal No.34 (UN 2014)

Volume benda putar yang terbentuk dari daerah di kuadran I yang dibatasi oleh kurva , sumbu y dan lingkaran x2 + y2 = 1, diputar mengelilingi sumbu y adalah …
  1. 4/60 π satuan volume
  2. 17/60 π satuan volume
  3. 23/60 π satuan volume
  4. 44/60 π satuan volume
  5. 112/60 π satuan volume

PEMBAHASAN :
Diketahui persamaan yang membatasi kurva  dan x2 + y2 = 1

Gambar kurva yang dimaksud pada soal, sebagai berikut: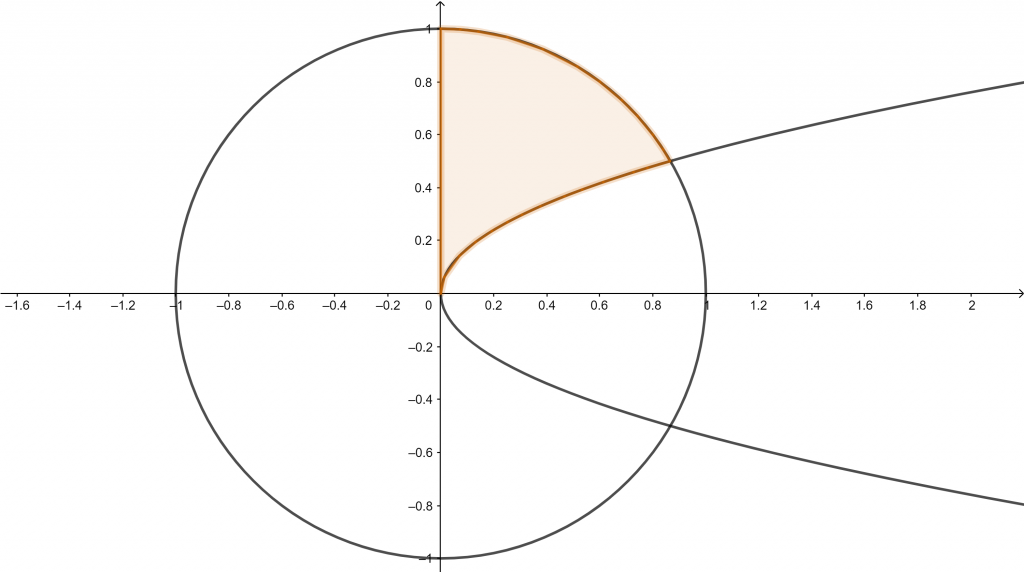

Titik potong: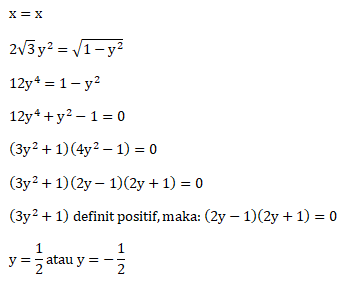

Dari gambar di atas, maka untuk menghitung volume benda  adalah sebagai berikut: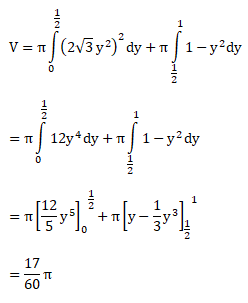

Jawaban : B

Soal No.35 (UN 2014)

Volume benda putar yang terbentuk dari daerah yang dibatasi oleh kurva , sumbu x, di dalam lingkaran x2 + y2 = 4 diputar mengelilingi sumbu x adalah …
  1. 80/15 π satuan volume
  2. 68/15 π satuan volume
  3. 64/15 π satuan volume
  4. 34/15 π satuan volume
  5. 32/15 π satuan volume

PEMBAHASAN :
Diketahui persamaan yang membatasi kurva  dan x2 + y2 = 4

Gambar kurva yang dimaksud pada soal, sebagai berikut: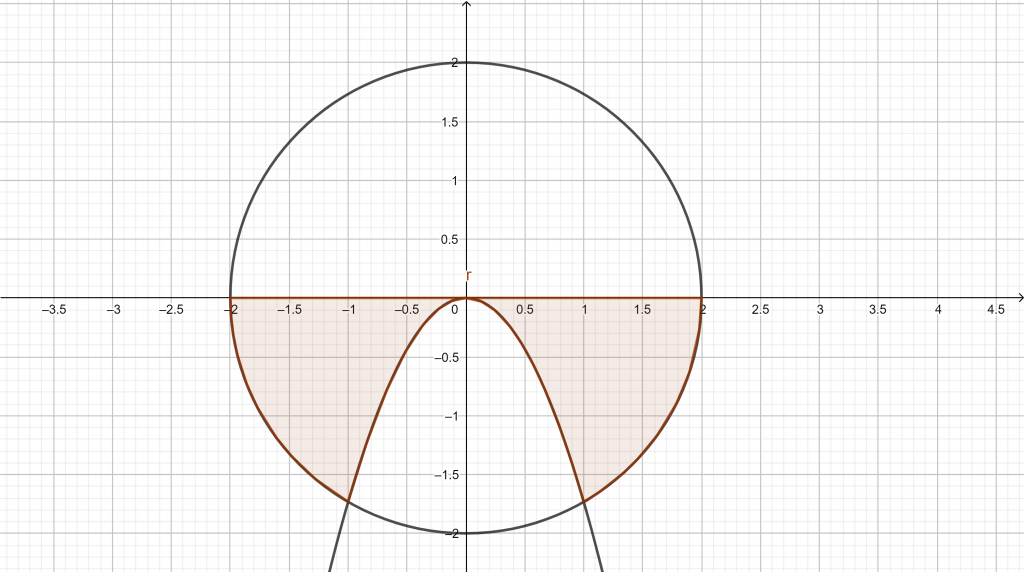

Titik potong: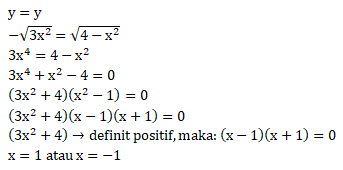

Dari gambar di atas, maka untuk menghitung volume benda  adalah sebagai berikut: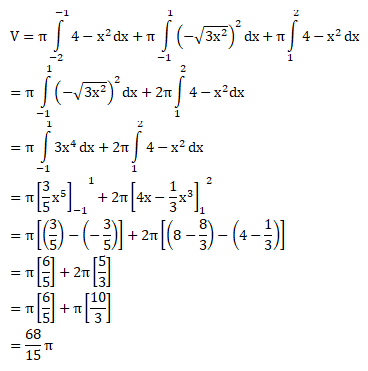

Jawaban : B

Soal No.36 (SNMPTN 2011)

PEMBAHASAN :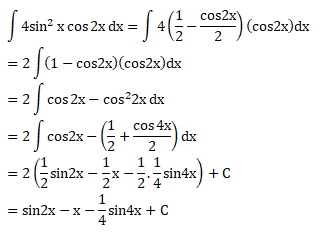

Jawaban : B

Soal No.37 (SNMPTN 2013)

Luas daerah yang dibatasi oleh kurva y = 6 – x2 dan y = |x|adalah …

PEMBAHASAN :
Diketahui persamaan yang membatasi kurva:  y = 6 – x2 dan y = |x|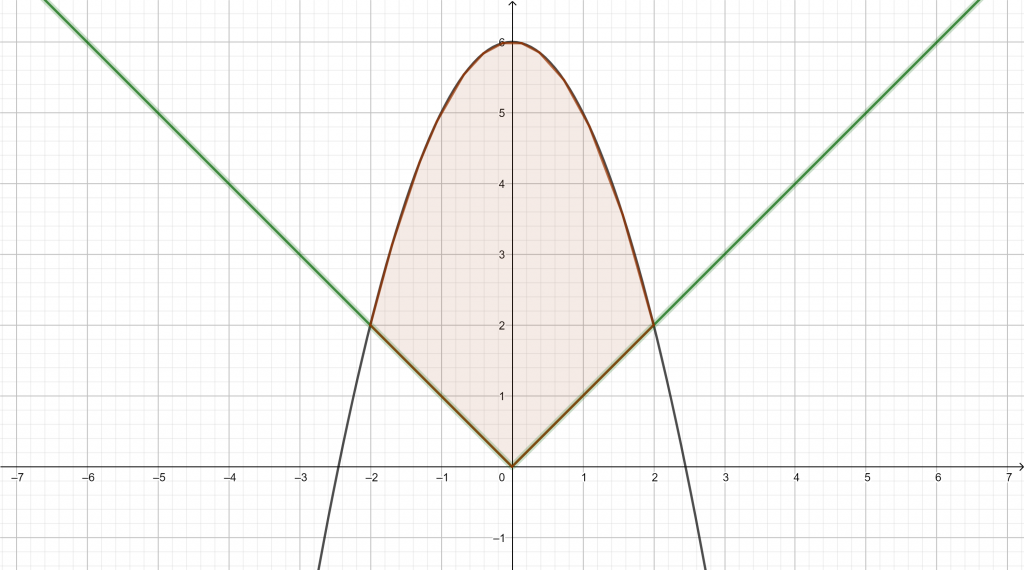

Titik perpotongan pada:

Jawaban : B

Soal No.38 (SBMPTN 2014)

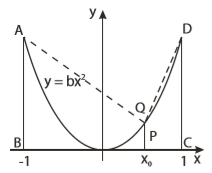
Misalkan A(t) menyatakan luas daerah di bawah kurva y = bx2 , 0 ≤ x ≤ t. Jika titik P(x ,0) sehingga A(x0 ) : A(1) = 1 : 8 maka perbandingan luas trapesium ABPQ : DCPQ = …

  1. 2 : 1
  2. 3 : 1
  3. 6 : 1
  4. 8 : 1
  5. 9 : 1

PEMBAHASAN :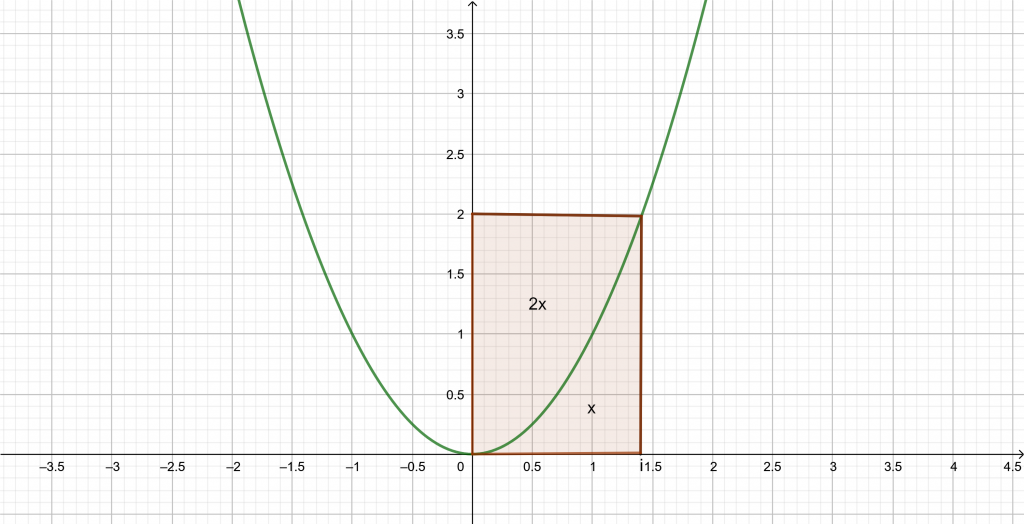

Pada grafik di atas dapat terlihat bahwa fungsi kuadrat membagi persegi panjang menjadi dua daerah dengan perbandingan 1 : 2

Maka:

Jawaban : B

Soal No.39 (SNMPTN 2011)

Luas daerah di bawah y = – x2 + 8x dan di atas y = 6x -24 dan terletak di kuadran I adalah …

PEMBAHASAN :
Diketahui persamaan y = – x2 + 8x dan y = 6x -24, terletak di kuadran I

Kurva yang terbentuk sebagai berikut: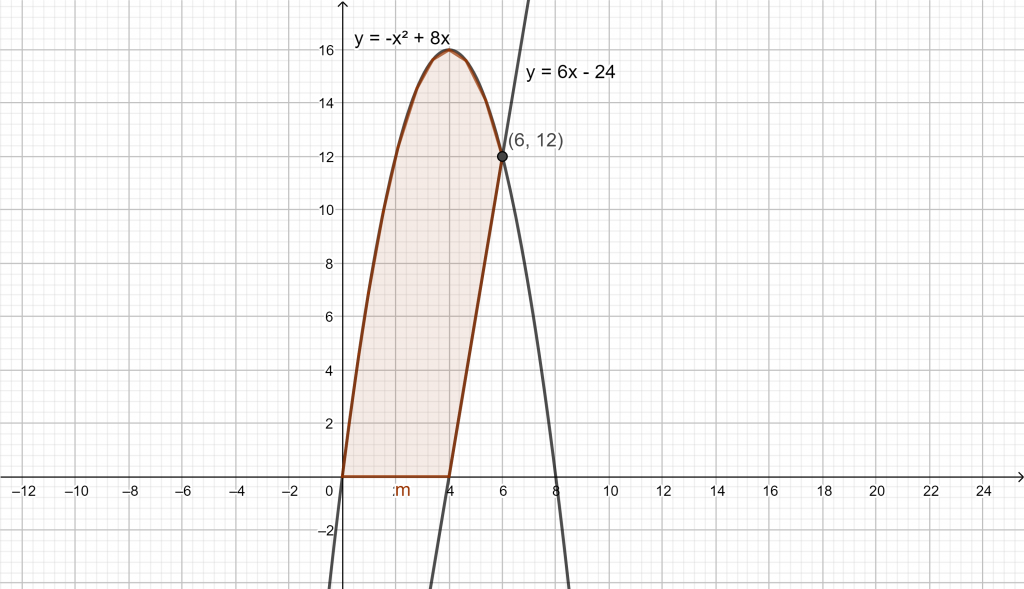

Titik perpotongan pada:
y = y
– x2 + 8x = 6x -24
x2 – 2x – 24 = 0
(x – 6) (x + 4) = 0
x = 6 atau x = -4

maka luas daerah yang dibatasi kurva adalah: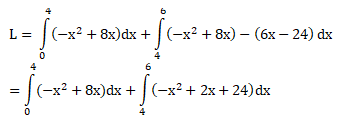

Jawaban : B

Soal No.39 (SNMPTN 2011)

Luas daerah di bawah y = – x2 + 8x dan di atas y = 6x -24 dan terletak di kuadran I adalah …

PEMBAHASAN :
Diketahui persamaan y = – x2 + 8x dan y = 6x -24, terletak di kuadran I

Kurva yang terbentuk sebagai berikut:

Titik perpotongan pada:
y = y
– x2 + 8x = 6x -24
x2 – 2x – 24 = 0
(x – 6) (x + 4) = 0
x = 6 atau x = -4

maka luas daerah yang dibatasi kurva adalah: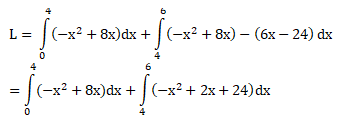

Jawaban : B

Soal No.40 (SIMAK UI 2011)

Jika daerah yang dibatasi oleh sumbu y, kurva y = x2 dan garis y = a2 dimana a ≠ 0 diputar mengelilingi sumbu x volumenya sama dengan jika daerah itu diputar mengelilingi sumbu y. nilai a yang memenuhi adalah …

  1. 5/8
  2. 3/8
  3. 2/5
  4. 8/5
  5. 5/2

PEMBAHASAN :
Penyelesaian I:
Mencari titik potong, yaitu:
y = y
x2 = a2
x2 – a2 = 0
(x – a)(x + a) = 0
x = a atau x = – a

penyelesaian II:
volume diputar terhadap sumbu x: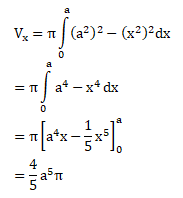

Penyelesaian III:
Volume diputar terhadap sumbu y:

Jawaban : A

Soal No.41 (UMPTN 2009)

  1. a
  2. 1 – a
  3. 2a
  4. a – ½
  5. a

PEMBAHASAN :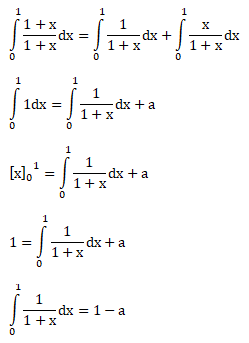

Jawaban : B

Soal No.42 (UM UGM 2008)

Gradien garis singgung suatu kurva di titik (x,y) sama dengan 2x + 5. Jika kurva ini melalui titik (2,20) maka kurva tersebut memotong sumbu x di …

  1. (2,0) dan (3,0)
  2. (-2,0) dan (-3,0)
  3. (2,0) dan (-3,0)
  4. (-2,0) dan (3,0)
  5. (-2,0) dan (2,0)

PEMBAHASAN :
Diketahui gradien garis = y’ = 2x + 5
∫ y =2x+5 dx  ⇒  x2 + 5x + C

titik yang dilalui kurva adalah titik (2,20), maka:
20 = 22 + 5(2) + C
20 = 14 + C
C = 6

Persamaan yang terbentuk adalah y = x2 + 5x + 6, memotong sumbu x jika y = 0
⇒ x2 + 5x + 6 = 0
⇒ (x + 3) (x + 2) = 0
x = -3 atau x = -2

sehingga koordinat titik yang memotong sumbu x adalah (-2,0) dan (-3,0)
Jawaban : B

Soal No.43 (UM UGM 2008)

Jika luas daerah yang dibatasi oleh kurva y = x2 dan y = (2m – 1)x adalah 4½ maka m = …

  1. 1½ atau -½
  2. 2 atau -1
  3. 2½ atau -1½
  4. 3 atau -2
  5. 3½ atau -2½

PEMBAHASAN :
Titik perpotongan pada:
y = y
⇒ x2 = (2m – 1)x
⇒ x2 – (2m – 1)x = 0
⇒ D = (-(2m – 1))2 – 4.1.0
⇒(2m – 1)2

Maka untuk menghitung luas, sebagai berikut: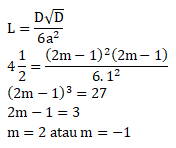

Jawaban : B

Soal No.44 (SPMB 2007)

Jika U1 , U2 , U3 , … berturut – turut adalah suku ke-1, ke-2, ke-3, … suatu barisan aritmetika dengan U3 – U1 = 6 dan U6 = 12 maka luas daerah yang dibatasi oleh kurva y = U1 X2 + U2 X + U3 dan sumbu x adalah …

  1. 3 satuan luas
  2. 4 satuan luas
  3. 5 satuan luas
  4. 6 satuan luas
  5. 7 satuan luas

PEMBAHASAN :
Diketahui barisan aritmetika dengan U3 – U1 = 6 dan U6 = 12

Persamaan untuk kurva y = U1 x2 + U2 x + U3
U3 – U1 = 6
(a + 2b) – a = 6
.                 b = 3
U6 = 12
a + 5b = 12
a + 5(3) = 12
.          a = – 3
sehingga, barisan aritmetika yang terbentuk adalah – 3, 0, 3 untuk persamaan y = U1 x2 + U2 x + U3 → -3x2 + 3

maka, untuk menghitung luas daerah sebagai berikut: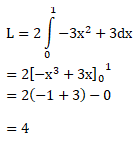

Jawaban : B

Soal No.45 (UMPTN 2004)

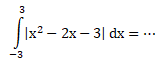
  2. 18
  3. 68/3
  4. 64/3
  5. 9

PEMBAHASAN :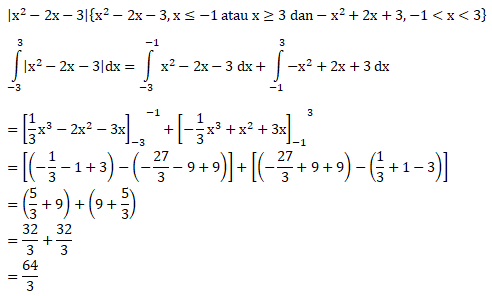

Jawaban : D

Soal No.46 (UMPTN 2003)

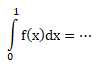
Diketahui ∫ f(x) dx = ax2 + bx + c, dan a≠0. Jika a, f(a), 2b membentuk barisan aritmetika, dan f(b) = 6 maka
  1. 17/4
  2. 21/4
  3. 25/4
  4. 13/4
  5. 11/4

PEMBAHASAN :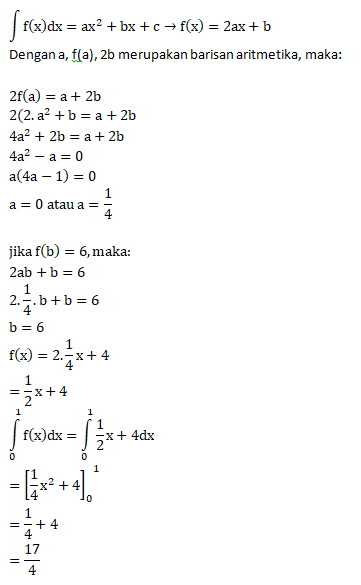

Jawaban : A

Semoga Bermanfaat

Related posts:

Artkel Terkait  Pembahasan Biologi UN 2014 No. 16

Leave a Reply

Your email address will not be published. Required fields are marked *