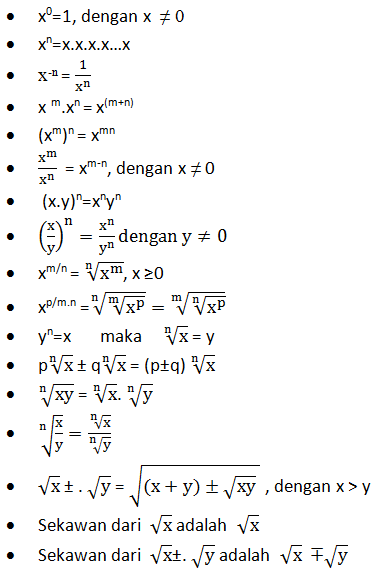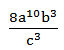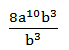Untuk Pembelajaran selanjutnya…
Eksponen
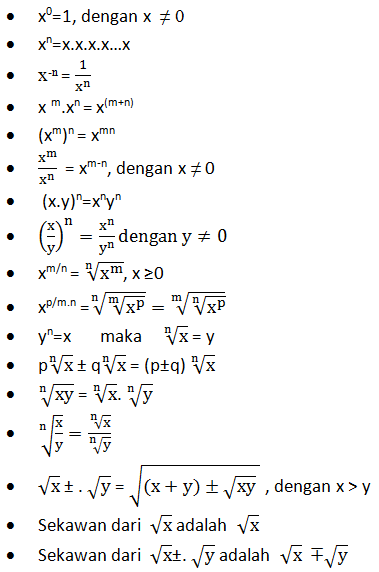
Logaritma
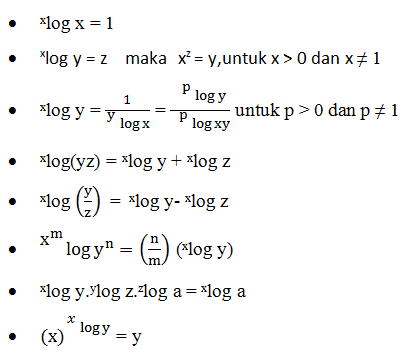
- Eksponen 1
- Eksponen 2
- Eksponen 3
- Eksponen 4
- Logaritma 1
- Logaritma 2
Soal No.1 (UTBK 2019)
Jika 0 < a < 1, maka![]()
mempunyai penyelesaian…
- x > loga 3
- x < -2 loga 3
- x < loga 3
- x > -loga 3
- x < 2 loga 3
PEMBAHASAN :![]()
![]()
⇒ 3 < ax
⇒ ax > 3
Karena 0 < a < 1
⇒ alog(ax) < alog(3)
⇒ x.alog a < alog 3
⇒ x. 1 < alog 3
⇒ x < loga 3
Jawaban C
Soal No.2 (UN 2014)
Bentuk sederhana dari 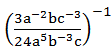 adalah…
adalah…
PEMBAHASAN :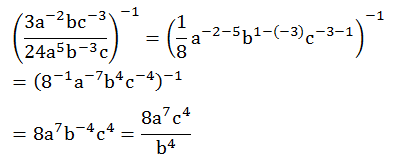
Jawaban : A
Soal No.3 (SNMPTN 2012 DASAR)
Jika blog a + blog a2 = 4 maka nilai alog b adalah …
- 3/4
- 1/2
- 4/3
- 2
- 3/2
PEMBAHASAN :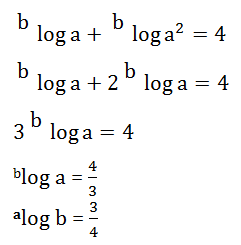
Jawaban : A
Soal No.4 (UN 2014)
Bentuk sederhana dari ![]() =…
=…
PEMBAHASAN :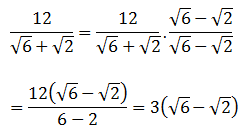
Jawaban : D
Soal No.5 (SBMPTN 2014 DASAR)
jika p = (alog 2)![]()
PEMBAHASAN :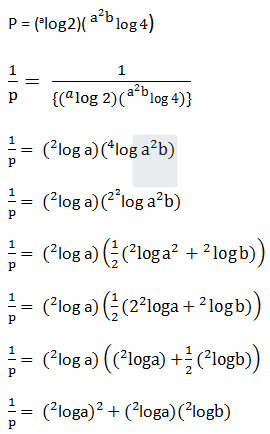
Jawaban : C
Soal No.6 (UN 2012)![]()
- 32
- 60
- 100
- 320
- 640
PEMBAHASAN :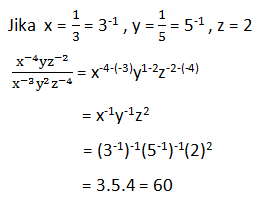
Jawaban : B
Soal No.7 (SIMAK UI 2009)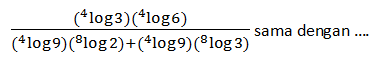
- 1/3
- 3/4
- 4/3
- 2
- 3
PEMBAHASAN :
Jawaban : B
Soal No.8 (UN 2014)
Hasil dari ![]()
- 11/4
- 15/4
- 17/4
- 11
- 15
PEMBAHASAN :
Jawaban : B
Soal No.9 (SNMPTN 2010 DASAR)
Jika n memenuhi  Maka(n-3)(n+2)=…
Maka(n-3)(n+2)=…
- 36
- 32
- 28
- 26
- 24
PEMBAHASAN :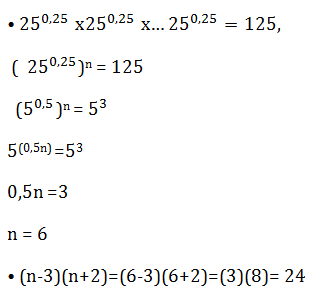
Jawaban : E
Soal No.10 (SBMPTN 2014 DASAR))
Jika 4x – 4x – 1 =6 maka (2x)˟ sama dengan …
- 3
- 3√3
- 9
- 9√3
- 27
PEMBAHASAN :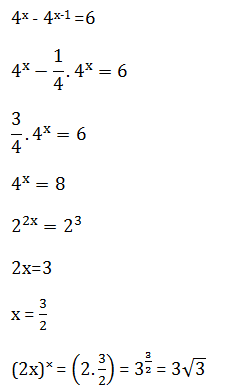
Jawaban : B
Soal No.11 (UM UGM 2008)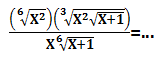

- x
- 1
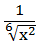

PEMBAHASAN :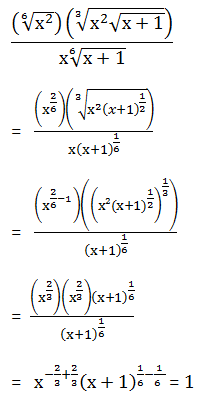
Jawaban : C
Soal No.12 (UM UGM 2009)![]()
- 3/5
- 5/3
- 1+ ablog ab²
- 1 + ablog a²b
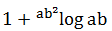
PEMBAHASAN :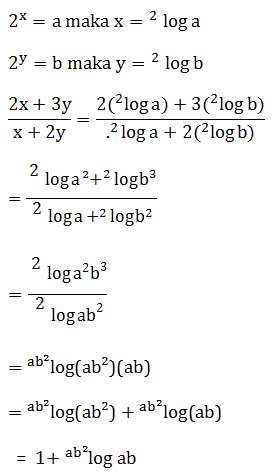
Jawaban : E
Soal No.13 (SNMPTN 2008 DASAR)
Dalam bentuk pangkat rasional 
PEMBAHASAN :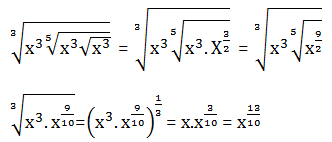
Jawaban : C
Soal No.14 (UN 2009)
Akar-akar persamaan 9x -12.3x + 27 = 0 adalah α dan β. Nilai αβ = …..
- -3
- -2
- 1
- 2
- 3
PEMBAHASAN :
9x − 12.3x + 27 = 0
(3x)2 − 12.3x + 27 = 0
Jika dimisalkan 3x = a, maka:
a2 − 12a + 27 = 0
(a-9)(a-3) = 0
a − 9 = 0
a = 9
3x = a = 9
3x = 32
x = 2 =α
dan
a − 3 = 0
a = 3
3x = a = 3
3x = 31
x = 1 = β
Maka:
αβ = 2.1 = 2
Jawaban : D
Soal No.15 (UN 2009)
Diketahui ![]() . Nilai x yang memenuhi persamaan itu adalah…..
. Nilai x yang memenuhi persamaan itu adalah…..
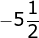
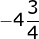
- 4
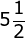
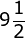
PEMBAHASAN :![]()
![]()
![]()
![]()
![]()
![]()
4x – 16 = 6
4x = 22![]()
Jawaban : D
Soal No.16 (UN 2008)
Himpunan penyelesaian dari pertidaksamaan eksponen 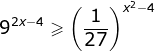 adalah….
adalah….
PEMBAHASAN :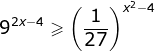
(32)2x-4 ≥ (3-3)x2-4
4x – 8 ≥ -3x2 + 12
3x2 + 4x – 20 ≥ 0
(3x + 10)(x − 2) ≥ 0![]() dan x = 2
dan x = 2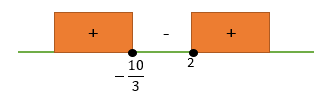
HP = ![]()
Jawaban : C
Soal No.17 (UN 2014)
Penyelesaian dari 32x+3 – 84.3x + 9 ≥ 0 adalah….
- -1 ≤ x ≤ 2
- -2 ≤ x ≤ 1
- x ≤ -2 atau x ≥ -1
- x ≤ -2 atau x ≥ 1
- x ≤ 1 atau x ≥ 2
PEMBAHASAN :
32x+3 – 84.3x + 9 ≥ 0
(3x)2.33 – 84. 3x + 9 ≥ 0
Jika dimisalkan 3x = a
27a2 + 84a + 9 ≥ 0
9a2 − 28a + 3 ≥ 0
(9a − 1)(a − 3) ≥ 0
a = 1/9 dan a = 3
Jika a = 1/9
3x = a = 1/9
3x = (1/3)2
x = -2
Jika a = 3
3x = a = 3
3x = 31
x = 1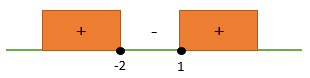
HP = x ≤ -2 atau x ≥ 1
Jawaban : D
Soal No.18 (UN 2014)
Himpunan penyelesaian dari 32x − 6.3x < 27 adalah….
- {x | x < -3, x ∈ R}
- {x | x < -2, x ∈ R}
- {x | x < 2, x ∈ R}
- {x | x > 2, x ∈ R}
- {x | x > 3, x ∈ R}
PEMBAHASAN :
32x − 6.3x < 27
32x − 6.3x − 27 < 0
Jika dimisalkan 3x = a
a2 – 6a – 27 < 0
(a − 9)(a + 3) < 0
a = 9 dan a = -3
Jika a = 9
3x = a = 9
3x = (3)2
x = 2
Jika a = -3
3x = a = -3
3x = -3
x = tidak memenuhi
Maka pilihannya tinggal x < 2 atau x > 2
Jika disubstitusikan nilai = 1 (x <2)ke pertidaksamaan 32x − 6.3x < 27
32.1 − 6.31 < 27
9 – 18 < 27
-9 < 27 (memenuhi)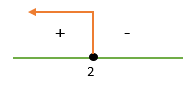
HP = x < 2
Jawaban : C
Soal No.19 (UN 2014)
Penyelesaian pertidaksamaan 3log x . 1-2xlog 9 > 2 − 1-2xlog 9 adalah….
- 0 < x <

- 0 < x <

- 0 < x <

 < x <
< x < 
 < x <
< x < 
PEMBAHASAN :
Syarat terpenuhi:
Jawaban : D
Soal No.20 (UN 2013)
Penyelesaian dari pertidaksamaan 25log (x-3) + 25log (x + 1) ≤ ½ adalah….
- -2 < x < 4
- -3 < x < 4
- x < -1 atau x > 3
- 3 < x ≤ 4
- 1 < x < 2 atau 3 < x < 4
PEMBAHASAN :
Syarat terpenuhi:
- x − 3 > 0, maka x > 3
- x + 1 > 0, maka x > -1
- 25log (x − 3) + 25log (x + 1) ≤ ½
25log ((x − 3)(x + 1)) ≤ 25log 25½
x2 − 2x − 3 ≤ 5
x2 − 2x − 8 ≤ 0
(x − 4)(x + 2) ≤ 0
x − 4 = 0
x = 4
atau
x + 2 = 0
x = -2
Maka garis bilangannya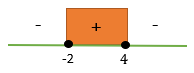
karena x > 3 dan x > -1 maka: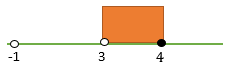
Sehingga penyelesaiannya
3 < x ≤ 4
Jawaban : D
Soal No.21 (SIMAK UI 2011)
Jika solusi dari persamaan 5x+5 = 7x dapat dinyatakan dalam bentuk x = alog 55, maka nilai a =….
PEMBAHASAN :
5x+5 = 7x
log 5x+5 = log 7x
(x + 5) log 5 = x.log 7
x log 5 + 5 log 5 = x log 7
5 log 5 = x log 7 − x log 5
5 log 5 = x log ![]()
log 55 = x log ![]()
![]()
x = alog 55 = 7/5log 55
maka a = ![]()
Jawaban : C
Soal No.22
Jika diketahui x = ¼, y = 3 dan c = -2. Maka nilai dari ![]() adalah….
adalah….
- 3.888


- 7.776

PEMBAHASAN :![]() = (x)2-(-1) . y-3-2 . z3-1
= (x)2-(-1) . y-3-2 . z3-1
. = (x)3 . (y)-5 . (z)2
. = (4-1)3 . (3)-5 . (-2)2
. = (4)-3 . (3)-5 . (-2)2
. = ![]()
Jawaban : B
Soal No.23
Bentuk sederhana dari ![]() ….
….
PEMBAHASAN :![]()
. ![]()
. ![]()
. ![]()
Jawaban : B
Soal No.24
Jika a = 2 dan b = 4, maka nilai dari  ….
….
PEMBAHASAN :
. ![]()
. ![]()
Untuk a = 2 dan b = 4, maka:
. ![]()
Jawaban : B
Soal No.25
Jika f(n) = 2n+2 . 4n-3 dan g(n) = 8n+1 dengan n adalah bilangan asli, maka ![]()
PEMBAHASAN :
Jawaban : B
Soal No.26
Bentuk ![]() dapat dituliskan tanpa eksponen negatif menjadi …
dapat dituliskan tanpa eksponen negatif menjadi …
PEMBAHASAN :
Jawaban : E
Soal No.27
Jika 9x =25, maka 3x+2 + 9x adalah …
- 50
- 60
- 80
- 70
- 40
PEMBAHASAN :
9x = 25
32x = 52
3x = 5
Maka 3x+2 + 9x = 3x . 32 + (3x)2
= 5. 32 + 52
= 45 + 25
= 70
Jawaban : D
Soal No.28
Jika p dan q adalah bilangan bulat positif yang memenuhi pq = 210 – 29 , maka p + q adalah …
- 10
- 11
- 12
- 13
- 14
PEMBAHASAN :
pq = 210 – 29
= 29 . (2 – 1)
= 29
p = 2 dan q = 9
Maka p + q = 2 + 9 = 11
Jawaban : B
Soal No.29
Bentuk pangkat rasional dari  adalah …
adalah …
PEMBAHASAN :
Jawaban : C
Soal No.30
Tentukan penyelesaian dari persamaan berikut!
PEMBAHASAN :

Penyelesaian 1
x2 – 2 = 0 → x = ± 2
Penyelesaian 2
2x + 1 = x – 3
2x – x = – 4
x = – 4
Maka himpunan penyelesaiannya = {2, -2, -4} x2 – 2x – 15 = 0
x2 – 2x – 15 = 0
(x + 3)(x – 5) = 0
x = -3
x = 5
Maka himpunan penyelesaiannya = {-3,5}
Penyelesaian 1
x – 2 = x2 + 8x + 10
x2 + 8x – x + 10 + 2 = 0
x2 + 7x + 12 = 0
(x + 4)(x + 3) = 0
x = – 4
x = – 3
Penyelesaian 2
Misalkan:
x + 3 = – 1 → x = – 4 (memenuhi)
x + 3 = 0 → x = – 3 (memenuhi)
x + 3 = 1 → x = – 2 (tidak memenuhi)
Maka himpunan penyelesaiannya = {- 4, – 3}
Soal No.31
Penyelesaian persamaan ![]() yaitu a dan b (a>b), maka a + b = …
yaitu a dan b (a>b), maka a + b = …
- 1
- 2
- 3
- 4
- 5
PEMBAHASAN :
x2 – 5x – 28 = 4(- x – 2)
x2 – 5x – 28 = – 4x – 8
x2 – 5x + 4x – 28 + 8 = 0
x2 – x – 20 = 0
(x + 4)(x – 5) = 0
x = – 4 → a
x = 5 → b
maka a + b = – 4 + 5 = 1
Jawaban : A
Soal No.32
Nilai x yang memenuhi persamaan  adalah …
adalah …
- 2
- 5
- -1
- 1
- -3
PEMBAHASAN :
6 + 2x – 6 = – 2x + 4
2x + 2x = 4
4x = 4
x = 1
Jawaban : D
Soal No.33
Jika x1 dan x2 penyelesaian dari persamaan 22x – 4.2x+1 – 20 = 0 (x1 > x2 ), maka nilai dari 3x1 – 2x2 adalah …
- 18
- 21
- 26
- 15
- 20
PEMBAHASAN :
22x – 4.22x+1 – 20 = 0
(2x)2 – 8(2x ) – 20 = 0
(2x +2)(2x – 10) = 0
2x = – 2
2x = 10
Maka 3x1 – 2x2 = 3(-2) – 2(10) = – 6 – 20 = – 26
Jawaban : C
Soal No.34
Himpunan penyelesaian persamaan 2.32x -3.3x+1 + 4 = 0 yaitu a dan b (a > b), maka a + b = …
PEMBAHASAN :
2.32x – 3.3x+1 + 4 = 0
2(3x )2 – 9(3x ) + 4 = 0
(2.3x – 1)(3x – 4) = 0
2.3x – 1 = 0 → 3x = ½
3x – 4 = 0 → 3x = 4
Maka a + b = ½ + 4 = 4 ½
Jawaban : B
Soal No.35
Akar-akar persamaan 3.22x – 12.2x – 36 = 0 adalah x1 dan x2 , maka nilai x1 – x2 = …
PEMBAHASAN :
3.22x – 12.2x + 24 = 0 , dibagi 3
22x – 4.2x + 8 = 0 , p = 2x
P2 – 4p – 8 = 0
p1.p2 = c/a
22x.22x = 8
22(x + x) = 23
2(x1 + x2) = 3
x1 + x2 =![]()
Jawaban : E
Soal No.36
Jika 32x + 3-2x = 14, maka 3x + 3-x adalah …
- 4
- 6
- 8
- 12
- 24
PEMBAHASAN :
Misalkan:
P = 3x + 3-x (kuadratkan di kedua ruas)
P2 = (3x + 3-x )2
P2 = 32x + 2 + 3-2x
P2 – 2 = 32x + 3-2x
32x + 3-2x = 14
P2 – 2 = 14
P2 = 16
P = 4
Maka nilai 3x + 3-x = p = 4
Jawaban : A
Soal No.37
Jika  , maka x = …
, maka x = …
- 3
- ½
- 5
- 1
- 2
PEMBAHASAN :
3.22x + 22x = 16
4.22x = 16
22x = 4
22x = 22
2x = 2
x = 1
Jawaban : D
Soal No.38
Akar-akar persamaan 9x+1 + 3x-2 = 27 adalah …
PEMBAHASAN :
9x+1 + 3x-2 = 27![]()
9x + 3x – 3 = 0
(3x )2 + 3x – 3 = 0, misalkan 3x = a
a2 + a – 3 = 0
a = 1, b = 1, c = – 3
Akar-akarnya dapat dihitung sebagai berikut:
Jawaban : A
Soal No.39
Himpunan penyelesaian dari pertidaksamaan eksponen ![]() adalah …
adalah …
PEMBAHASAN :
2(2x – 3) ≥ – 3(x2 – 3)
4x – 6 ≥ – 3x2 + 9
4x – 6 + 3x2 – 9 ≥ 0
3x2 + 4x – 15 ≥ 0
(3x – 5)(x + 3) ≥ 0
Maka himpunan penyelesaiannya![]()
Jawaban : C
Soal No.40
Penyelesaian pertidaksamaan 32x+1 – 5.3x+1 + 18 ≥ 0 adalah …
- x ≤ – 2 atau x ≤ 3
- x ≤ 2 atau x ≥ 3
- x ≥ 3 atau x ≥ 1
- x ≤ – 1 atau x ≤ 3
- x ≤ 0 atau x ≥ -1
PEMBAHASAN :
32x+1 – 5.3x+1 + 18 ≥ 0
3.32x – 5.(3.3x ) + 18 ≥ 0 → dibagi 3
32x – 5.3x + 6 ≥ 0
(3x )2 – 5(3x ) + 6 ≥ 0
(3x – 2)(3x – 3) ≥ 0
3x ≤ 2 atau 3x ≥ 3, 3x = x
x ≤ 2 atau x ≥ 3
Jawaban : B
Soal No.41
Penyelesaian pertidaksamaan 54x – 6.52x + 8 < 0 adalah …
- x > 1 atau x > 3
- x < 2 atau x > – 4
- x > – 3 atau x > 2
- x > 2 atau x > 4
- x < 0 atau x < 1
PEMBAHASAN :
54x – 6.52x + 8 < 0
(52x )2 – 6.52x + 8 < 0
(52x – 2)(52x – 4) < 0
2 < 52x < 4
21 < 52x < 22
x > 2 atau x > 4
Jawaban : D
Semoga Bermanfaat