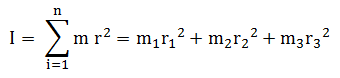Untuk Pembelajaran selanjutnya…
Hey kamu yang baru jadi kelas XI. Sekarang di mata pelajaran fisika bab pertama yang dipelajari adalah bab dinamika rotasi dan kesetimbangan benda tegar. Ngapain aja sih, simak ringkasan materi dan 15 contoh soal dinamika rotasi dan kesetimbangan benda tegar. Biar ga bingung kamu juga bisa liat-liat di daftar isinya yah.
Momen Gaya
Momen gaya merupakan salah satu bentuk usaha dengan salah satu titik sebagai titik acuan. Momen gaya merupakan hasil kali gaya dan jarak terpendek arah garis kerja terhadap titik tumpu. Momen gaya sering disebut dengan momen putar atau torsi, diberi lambang τ (dibaca: tau).
τ = F . d
Satuan dari momen gaya atau torsi ini adalah N . m atau joule.
Momen Inersia Benda Tegar
Momen inersia yaitu ukuran kelembapan suatu benda untuk berputar. Rumusannya yaitu sebagai berikut:
I = mr2
Keterangan:
I = momen inersia benda tegar(kg m2)
m = massa benda (kg)
r = jarak massa ke sumbu putar (m)
Momen inersia bergantung pada :
- Bentuk benda
- Massa benda
- Letak sumbu putar
Jika terdapat banyak partikel maka momen inersia totalnya dapat dirumuskan sebagai berikut:
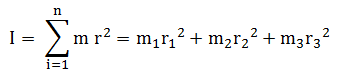
Momen inersia benda tegar dapat dihitung menggunakan teknik integral dengan persamaan :
![]()
Untuk benda-benda yang beraturan bentuknya, momen inersianya dapat ditentukan sesuai dengan tabel :
Momen inersia benda terhadap sembarang sumbu rotasi yang paralel dengan sumbu pusat massa menggunakan teorema sumbu paralel.
I = Ipm + Md2
Keterangan :
I = momen inersia (kg m2)
Ipm = momen inersia pusat massa (kg m2)
M = massa benda (kg)
d = jarak sumbu rotasi ke pusat massa (m)
Momentum Sudut
Momentum sudut merupakan hasil kali antara momen inersia dan kecepatan sudut. Dirumuskan sebagai berikut:
L = I.ω
Keterangan :
L = momentum sudut (kg m2 rad/s)
I = momen inersia (kg m2)
ω = kecepatan sudut (rad/s)
Hubungan Momen Gaya dan Percepatan Sudut
Hubungan antara momen gaya dengan percepatan sudut memenuhi persamaan Hukum II Newton pada gerak translasi. Pada gerak rotasi, berlaku hubungan
τ = I . α
Keterangan:
τ = momen gaya (Nm)
I = momen inersia ( kg m2)
α = percepatan sudut (rad/s2)
Energi Kinetik Sudut
Yaitu energi kinetik yang dimiliki oleh benda yang berotasi, dirumuskan sebagai berikut:
EKrot = ½ I.ω2
Keterangan:
EKrot = energi kinetik rotasi (joule)
I = momen inersia (kg m2)
ω = kecepatan sudut (rad/s)
Gabungan Energi Kinetik
Ketika benda menggelinding maka benda memiliki kecepatan linier v untuk bergerak translasi dan kecepatan sudut untuk bergerak rotasi. Besar energi kinetik totalnya dirumuskan sebagai berikut:
EK = EKtrans + EKrot
EK = mv2 + Iω
Keterangan:
EK = energi kinetik (joule)
EKrot = energi kinetik rotasi ( joule )
EKtrans = energi kinetik transiasi (joule)
I = momen inersia (kg m2)
= kecepatan sudut (rad/s)
m = massa benda (kg)
v = kecepatan linier (m/s)
Hukum Kekekalan Momentum Sudut
Dijelaskan bahwa apabila tidak ada momentum gaya yang bekerja pada sistem, maka momentum sudut akan konstan.
L1 = L2
I1 ⍵1 = I2 ⍵2
Keterangan:
L1 = momentum sudut awal (kg m2 rad/s)
I1 = momen inersia awal (kg m2)
⍵1 = kecepatan sudut awal (rad/s)
L2 = momentum sudut akhir (kg m2 rad/s)
I2 = momen inersia akhir (kg m2)
⍵2 = kecepatan sudut akhir (rad/s)
Dinamika Rotasi
Jika benda dalam keadaan diam atau setimbang dan bergerak kelajuan konstan maka berlaku:
ΣF = 0 dan Στ = 0
Namun jika benda bergerak dengan percepatan tetap maka,
ΣF = m a dan Στ = I. α
Titik Berat Benda
Titik Berat Benda adalah titik tangkap gaya berat benda dimana dipengaruhi oleh medan magnet.
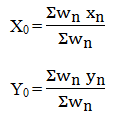
Keterangan :
X0 = letak titik benda pada sumbu x
Wn = berat benda ke-n
Xn = letak titik berat benda ke-n pada sumbu x
Y0 = letak titik berat benda ke sumbu y
Yn = letak titik berat benda ke-n pada sumbu y
Untuk nilai percepatan gravitasi g yang dapat dianggap konstan,maka titik pusat massa dirumuskan sebagai berikut:

Keterangan :
Xpm = pusat massa benda pada sumbu x
mn = massa benda ke-n
xn = pusat massa benda ke-n pada sumbu x
Ypm = pusat massa benda pada sumbu y
yn = pusat massa benda ke-n pada sumbu y
Titik berat benda homogen :
- Benda berbentuk ruang ( dimensi tiga)
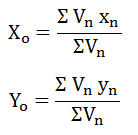
Keterangan:
x0 = titik berat benda pada sumbu x
Vn = volume benda ke-n
xn = titik berat benda ke-n pada sumbu x
Y0 = titik berat benda pada sumbu y
Yn = titik berat benda ke-n pada sumbu y
- Benda berbentuk luasan (dimensi dua)
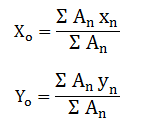
Keterangan:
X0 = titik berat benda pada sumbu x
An = luas benda ke-n
Xn = titik berat benda ke-n pada sumbu x
Y0 = titik berat benda pada dumbu y
Yn = titik berat benda ke-n pada sumbu y
- Benda berbentuk garis (dimensi satu)
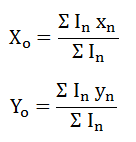
Keterangan:
X0 = titik berat benda pada sumbu x
In = panjang benda ke-n
Xn = titik berat benda ke-n pada sumbu x
Y0 = titik berat benda pada sumbu y
Yn = titik berat benda ke-n pada sumbu y
Titik Berat Benda Teratur
Titik berat bentuk teratur linear

Titik berat benda teratur berbentuk luas bidang homogen
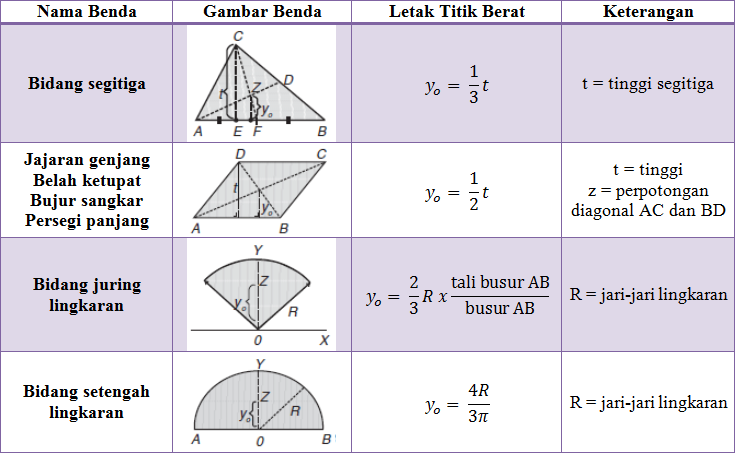
Titik berat benda teratur berbentuk bidang ruang homogen
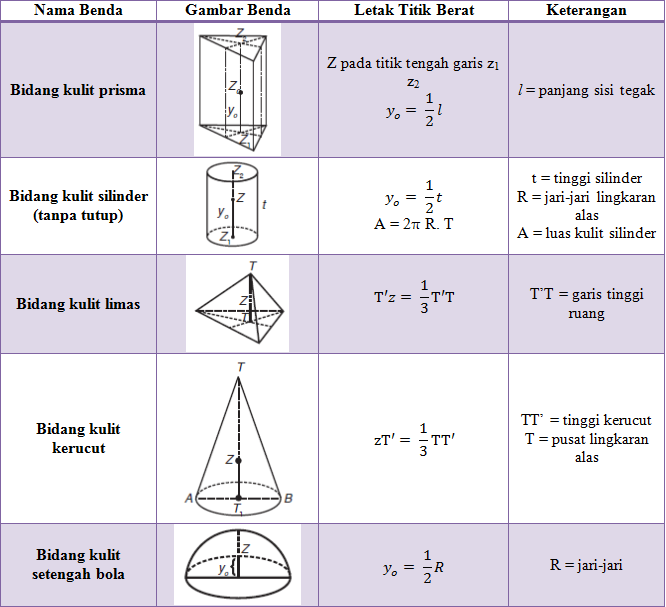
Soal No.1 (UTBK 2019)
Sebuah silinder bermassa 5 kg dengan jari-jari 50 cm berada dalam celah lantai miring seperti ditunjukkan gambar. Sudut kemiringan salah satu sisi lantai adalah θ (tan θ = ¾). Jika silinder ditarik dengan gaya horizontal F = 90 N dan momen inersia relatif terhadap titik A adalah 2,0 kgm2, percepatan sudut sesaat silinder relatif terhadap titik A adalah…
- 3,0 rad/s2
- 3,5 rad/s2
- 4,0 rad/s2
- 4,5 rad/s2
- 5,0 rad/s2
PEMBAHASAN :
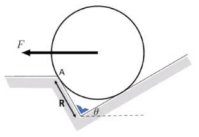
Menggambarkan gaya – gaya yang terlibat pada benda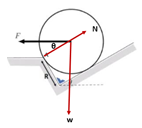
Momen gaya τ = F R Sin θ
Dengan ketentuan: Searah jarum jam negatif, berlawanan jarum jam positif
Jumlah Momen gaya pada titik A (gaya di titik itu bernilai τN = 0)
Στ = τF + τW
Στ = F R sin θF – w R sin θw
Στ = F R sin θ – w R sin (90 – θ)
Στ = F R sin θ – w R Cos θ
Dari soal:
tan θ = ¾ maka sin θ = 3/5 dan cos θ = 4/5
m = 5 kg maka w = 50 N
F = 90 N
R = 0,5 meter
Στ = F R sin θ – w R Cos θ
Στ = 90 0,5 3/5 – 50 0,5 4/5
Στ = 27 – 20
Στ = 7 Nm
Hubungan dengan momen inersia, I
Στ = I α
7 = 2α
α = 3,5 rad/s2
Jawaban B
Soal No.2 (UN 2013)
Dua bola masing masing massanya m1 = 2 kg dan m2 = 3 kg di hubungkan dengan batang ringan tak bermassa seperti pada gambar.
Jika sistem bola diputar pada sumbu di titik a maka besar momen inersia sistem bola adalah….
- 0,24 kg.m2
- 0,27 kg.m2
- 0,30 kg.m2
- 0,31 kg.m2
- 0,35 kg.m2
PEMBAHASAN :
Diketahui:
r1 = 0,2 m
r2 = 0,3 m
Menentukan momen inersia total
I=m1 r12+ m2 r12
I=2(0,2)2 +3(0,3)2
I=0,08+0,27
I=0,35 kg.m2
Jawaban : E
Soal No.3 (UM UGM 2008)
Batang homogen bermassa m, dalam kondisi setimbang sepeti pada gambar.
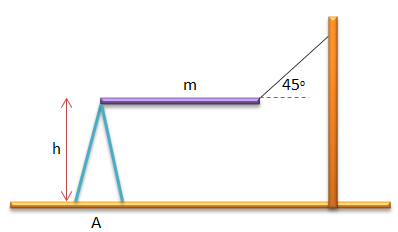
Dengan percepatan gravitasi g, besar torsi yang dialami tiang penumpu terhadap titik tancapnya, A adalah ….
- 4 mgh
- 2 mgh
- mgh
- mgh/2
- mgh/4
PEMBAHASAN :
Untuk menyelesaikan soal tersebut perhatikan gambar berikut!
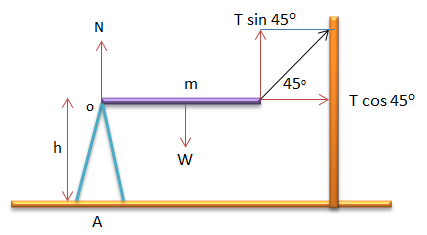

Jawaban : D
Soal No.4 (UN 2008)
Gaya F1 , F2 , F3 bekerja pada batang ABCD seperti pada gambar!
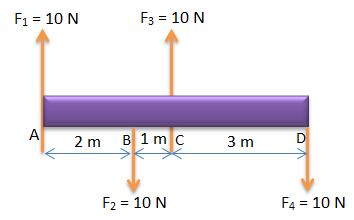
Jika massa batang diabaikan, maka nilai momen gaya terhadap titik A adalah…
- 15 N.m
- 18 N.m
- 35 N.m
- 53 N.m
- 68 N.m
PEMBAHASAN :
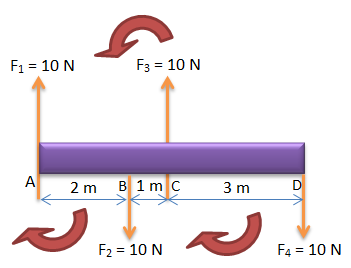

Jawaban : D
Soal No.5 (UM UGM 2008)
sistem katrol sepeti pada gambar, katrol tanpa silinder pejal homogen yang dapat berotasi tanpa gesekan terhadap sumbunya yang tetap. Massa beban m1 = m, massa katrol M = 2m, massa beban m2 = 3 m dan diameter katrol d. Bila percepatan gravitasi g dan sistem bergerak tanpa pengaruh luar ,percepatan sudut rotasi katrol sebesar ….
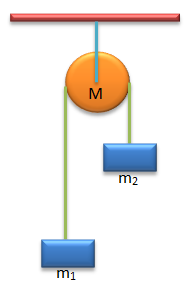
- 2g/5d
- 3g/5d
- 4g/5d
- 6g/5d
- g/d
PEMBAHASAN :

Jawaban : C
Soal No.6 (UN 2014)
Sebuah katrol dari sebuah pejal dengan tali yang dililitkan pada sisi luarnya ditampilkan seperti gambar.

Gesekan katrol diabaikan. Jika momen inersia katrol I = β dan tali ditarik Dengan gaya tetap F maka nilai F setara dengan…
- F = α. Β.R
- F = α. Β2.R
- F = α. (Β.R)-1
- F = α. Β.(R)-1
- F = (α. Β)-1.R
PEMBAHASAN :
Menentukan gaya F dari persamaan torsi:
τ = I α = F. R
Karena I = β, maka
R . F = α. β
F = α. β.(R)-1
Jawaban : D
Soal No.7 (SIMAK UI 2013)

Balok m1 = 3 kg dan balok m2 = 4 kg dihubungkan dengan tali melalui sebuah katrol (momen inersia katrol I = MR2) Seperti pada gambar. Massa katrol = 2 kg, jari – jari katrol R = 10 cm, dan percepatan gravitasi g = 10 m/s2. Kecepatan balok setelah bergerak sejauh 40 cm adalah ….
- 1 m/s
- √2 m/s
- 2 m/s
- √6 m/s
- 4 m/s
PEMBAHASAN :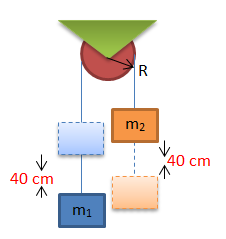

Jawaban : A
Soal No.8 (UN 2012)
Letak titik berat bangun bidang seperti pada gambar di samping dari sumbu X adalah..
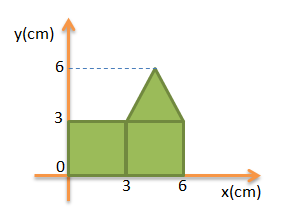
- 4,5 cm
- 4 cm
- 3,5 cm
- 3 cm
- 2 cm
PEMBAHASAN :
Gambar di bagi menjadi dua bagian
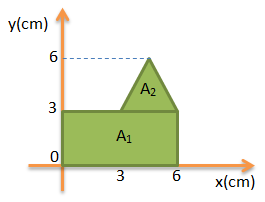

Jawaban : E
Soal No.9 (UM UGM 2013)
Benda bermassa M berbentuk silinder pejal/massif homogen dengan jari – jari R diliit dengan tali halus (massa tali diabaikan). Ujung tali dimatikan di titik tetap dan benda dibiarkan terjatuh berotasi seperti gambar. Dengan percepatan gravitasi g, besar tegangan tali pada sistem tersebut adalah …

- Mg
- 2Mg/3
- Mg/2
- Mg/3
- Mg/4
PEMBAHASAN :
Jawaban : D
Soal No.10 (UN 2009)
Sebuah katrol pejal bermassa (M) dan jari-jarinya (R) seperti pada gambar! Salah satu ujung tak bermassa dililitkan pada katrol,ujung tali yang tali di gantungi beban m kg percepatan sudut katrol (α), jika beban dilepas. Jika pada katrol ditempelkan plastisin A yang yang bermassa M, untuk menghasilkan percepatan sudut yang sama beban harus dijadikan…
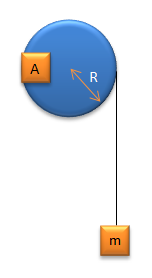
- 3/4 m kg
- 3/2 m kg
- 2 m kg
- 3 m kg
- 4 m kg
PEMBAHASAN :

Jawaban : C
Soal No.11 (UMB PTN 2009)
Papan loncat serbamasa sepanjang 4 m bermasa 50 kg ditahan dua tempat A dan B seperti pada gambar. Jarak A dan jarak B adalah 0,5 m dan jarak B ke C adalah 3 m. Seorang peloncat indah meloncat dan ujung papan loncat di titik C dengan menjejakan kakinya 103 N (papan diangap tegar). Gaya yang diberikan penahan di titik A pada saat peloncat indah tersebut menjejakan kakinya ke papan loncat adalah …..
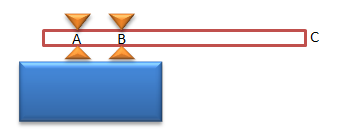
- 8,0 kN
- 7,5 kN
- 7,0 kN
- 6,5 kN
- 6,0 kN
PEMBAHASAN :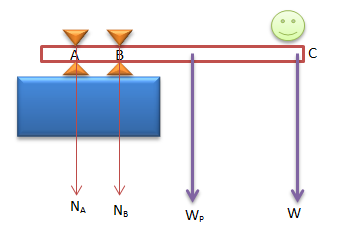
Titik berat papan yaitu di titik O, dimana titik O = ½ x panjang papan = ½ x 4 m = 2m
AB = 0,5 m
BC = 3 m,
OB = 1 m,
berat papan Wp= 500 N,
berat orang W= 103 N
sumbu rotasi yaitu titik B, syarat kesetimbangan adalah:
∑τ=0
AB. NA – OB.Wp -BC.W=0
0,5. NA – 1(500)- 3(1.000)=0
NA = 7.000 N = 7,0 kN
Jawaban : C
Soal No.12 (UN 2005)
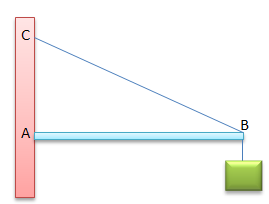
Pada sistem kesetimbangan benda tegar seperti pada gambar tersebut, batang A homogen dengan panjang 80 cm beratnya 18N pada ujung B digantung beban yang beratnya 30 N. Batang ditahan oleh tali BC jika jarak AC = 60 cm , tegangan pada tali adalah…
- 36 N
- 48 N
- 50 N
- 65 N
- 80 N
PEMBAHASAN :

Jawaban : D
Soal No.13 (UMPTN 1994)
Sumbu kedua roda muka dan sumbu kedua roda belakang sebuah truk yang bermasa 1.500 kg berjarak 2m. Pusat massa truk 1,5 m di belakang roda muka. Diandaikan bahwa percepatan gravitasi bumi 10 m/s2 beban yang dipikul oleh kedua roda muka truk itu sama dengan ……
- 1.250N
- 2.500N
- 3.750N
- 3.750N
- 6.250N
PEMBAHASAN :
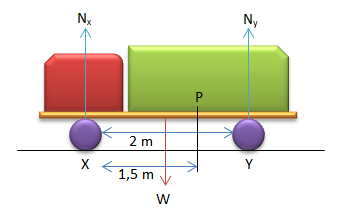
Diketahui :
XY = 2 m
PY = 0,5 m
PX = 1,5 m
W = m.g = 1.500 x 10 = 15.000 N
Syarat kesetimbangan :
∑τ=0
W(PY) – Nx(AB)=0
15.000(0,5)- Nx (2) = 0
Nx = 3.750 N
Jawaban : C
Soal No.14 (UN 2014)
Sebuah benda berbentuk silinder berongga (I = mR2) bergerak menggelinding tanpa tergelincir mendaki bidang miring kasar dengan kecepatan awal 10 m.s-1 , bidang miring itu mempunyai sudut elevasi α dengan tan α = 0,75. Jika gravitasi g = 10 m.s-1 dan kecepatan benda itu berkurang menjadi 5 m.s-1 maka jarak pada bidang miring yang ditempuh benda tersebut adalah…
- 12,5 m
- 10 m
- 7,5 m
- 5 m
- 2,5 m
PEMBAHASAN :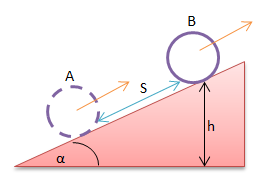
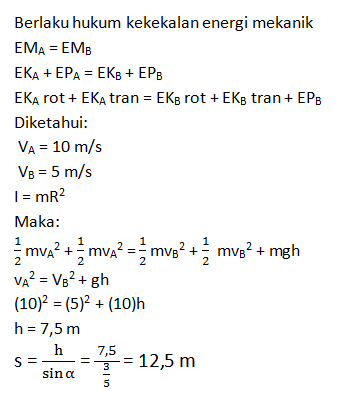
Jawaban : A
Soal No.15 (SNMPTN 2009)
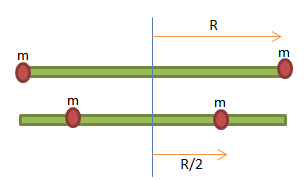
Sistem berputar dengan kecepatan sudut ω ketika kedua masa m berjarak sejauh R dari sumbu. Masa secara simultan ditarik sejauh R/2 mendekati sumbu oleh gaya yang arah nya sepanjang batang. Berapakah kecepatan sudut baru sistem?
- ω/4
- ω/2
- ω
- 2ω
- 4ω
PEMBAHASAN :
Jawaban : E
Soal No.16 (SNMPTN 2009)

Sebuah tangga homogen dengan panjang L diam bersandar pada tembok yang licin di atas lantai yang kasar dengan koefisien gesekan statis antara lantai dan tangga adalah μ. Jika tangga membentuk sudut θ tepat saat akan tergelincir, besar sudut θ adalah….

- tan θ = 2μ


- cos θ = μ
PEMBAHASAN :
Syarat setimbang pada keadaan diam
ΣF = 0
Sumbu x
ΣFx = 0
NB − fs = 0
NB = μ. NA ………. persamaan 1
Sumbu y
ΣFy = 0
NA − W = 0
NA = W ……….persamaan 3
Kesetimbangan rotasi, Στ = 0 berporos di A
½ L cos θ. W − L sin θ. NB = 0……persamaan 3
Substitusi persamaan 1 dan 2 ke persamaan 3
½ cos θ. W = sin θ. μ W![]()
![]()
Jawaban : C
Soal No.17 (UN 2013)

- 2 N.m
- 4 N.m
- 6 N.m
- 8 N.m
- 10 N.m
PEMBAHASAN :
Diketahui:
FA = FC = 10 N
FB = 20 N
AB = BC = 20 cm
Arah putar benda
Menentukan besar momen gaya bidang terhadap titik A
Στ = τA + τB + τC
Στ = IAFA + IBFB + ICFC sin 30o
Στ = 0 − 0,2(20) − 0,4(10) sin 30o
Στ = − 6 N.m (tanda (-) menunjukkan arah putaran searah jarum jam)
Jawaban : C
Soal No.18 (UN 2014)

Jika massa batang diabaikan dan panjang batang 4 m, maka nilai momen gaya terhadap sumbu putar di titik C adalah….
- 12 N.m
- 8 N.m
- 6 N.m
- 2 N.m
- Nol
PEMBAHASAN :
Diketahui:
F1 = 5 N
F2 = 0,4 N
F3 = 40 N
Arah putar benda untuk pusat di titik C
Menentukan besar momen gaya untuk pusat di titik C
Στ = τ1 + τ2 + τ3
Στ = I1F1 sin 53o + I2F2 + I3F3
Στ = 2(5 sin 53o) − 1(0,4) − 2(4,8)
Στ = − 2 N.m (tanda (-) menunjukkan arah putaran searah jarum jam)
Jawaban : D
Soal No.19 (UN 2014)

PEMBAHASAN :
Untuk memudahkan kita bagi dua bidang
Bidang 1 = bidang segi empat tanpa lubang (garis ungu)
Bidang 2 = bidang segi empat berlubang (garis jingga)
Bidang I
x = 3 (titik berat benda pada sumbu x)
y = 4 (titik berat benda pada sumbu y)
Luas (A) = 6 x 8 = 48
Ax = A.x = 48 x 3 = 144
Ay = A.y = 48 x 4 = 192
Bidang II
x = 3 (titik berat benda pada sumbu x)
y = 5 (titik berat benda pada sumbu y)
Luas (A) = 2 x 6 = 12
Ax = A.x = 12 x 3 = 36
Ay = A.y = 12 x 5 = 60
Menentukan x dan y bidang yang diarsir
ΣAx = Ax I – Ax II = 144 – 36 = 108
ΣAy = Ay I – Ay II = 192 – 60 = 132![]()
![]()
Jawaban : E
Soal No.20 (UN 2014)

- (0 ; 20) cm
- (0 ; 20,5) cm
- (0 ; 25) cm
- (0 ; 35) cm
- (0 ; 50) cm
PEMBAHASAN :
Untuk memudahkan kita bagi dua bidang
Bidang 1 = bidang tabung
Bidang 2 = bidang kerucut
Bidang I (tabung)
x = 0 (titik berat benda pada sumbu x terhadap titik o)
y = ½.40 = 20 cm(titik berat benda pada sumbu y terhadap titik o)
Volume (V) = πR2t = π(10)240 = 4000π
Vx = V.x = 4000π x 0 = 0
Vy = V.y = 4000π x 20 = 80.000π
Bidang II (kerucut)
x = 0 (titik berat benda pada sumbu x terhadap titik o)
y = 40 + ¼.30 = 47,5 cm (titik berat benda pada sumbu y)
Volume (V) = ![]() πR2t =
πR2t = ![]() π(10)230 = 1000π
π(10)230 = 1000π
Vx = V.x = 1000π x 0 = 0
Vy = V.y = 1000π x 47,5 = 47.500π
Menentukan x dan y benda
ΣVx = Vx I + Vx II = 0 + 0 = 0
ΣVy = Vy I + Vy II = 80.000π + 47.500π = 127.500π![]()
![]()
Jawaban : B
Semoga Bermanfaat