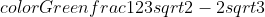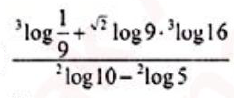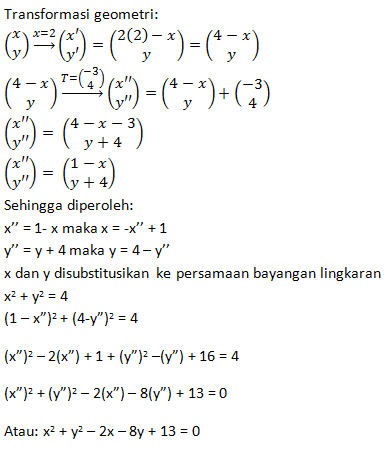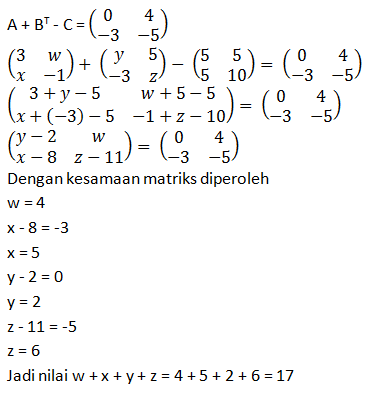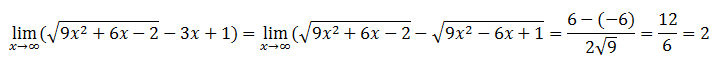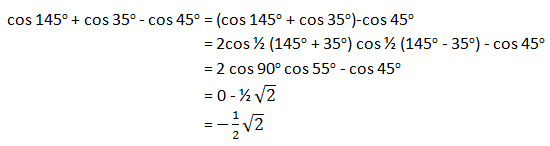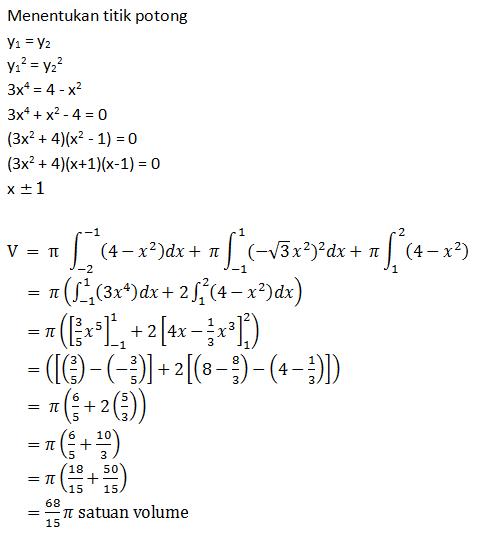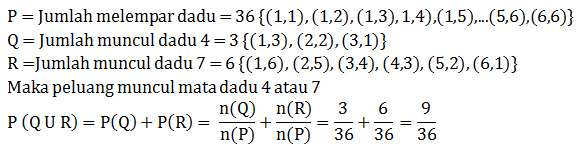Untuk Pembelajaran selanjutnya…
Soal No.1
PEMBAHASAN :
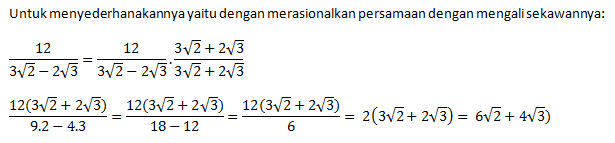
JAWABAN C
Soal No.2
PEMBAHASAN :
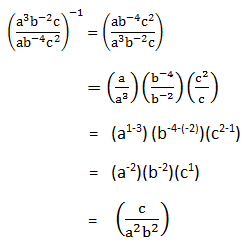
JAWABAN E
LIHAT JUGA : Try Out Online UN
Soal No.3
- 2
- 6
- 10
- 14
- 16
PEMBAHASAN :
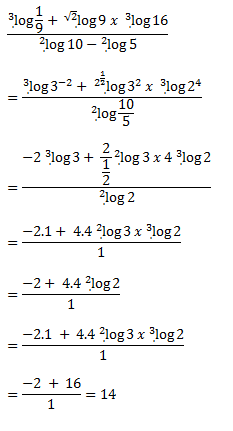
JAWABAN D
LIHAT JUGA : Try Out UN Matematika
Soal No.4
Himpunan penyelesaian dari 32x – 6.3x < 27 adalah….
- {x|x< -3, x E R}
- {x|x< -2, x E R}
- {x|x< 2, x E R}
- {x|x>2, x E R}
- {x|x> 3, x E R}
PEMBAHASAN :
Jika dimisalkan, a = 3x
32x – 6.3x < 27
(3x)2 – 6.3x < 27
a2 – 6a < 27
a2 – 6a – 27 < 0
(a-9)(a+3) < 0
a = 9
a = -3 (tidak memenuhi)
yang memenuhi yaitu a = 9
3x < 32
x < 2
JAWABAN C
Soal No.5
Akar-akar persamaan x2 + (p+1)x – 18 = 0 adalah α dan β, Jika α + 2 β = 0 dan p ≥ 0, nilai p = ….
PEMBAHASAN :
diketahui : a = 1, b = (p+1), c = -18, disubstitusikan ke α + 2β = 0
α2– 36 = 0
α2 = 36
α = ± 6
Menentukan β
Substitusikan ke α.β = -18
Untuk α = + 6
+6.β = -18
β = -3
Untuk α = – 6
-6.β = -18
β = +3
Menentukan p
Substitusikan ke α + β = -(p+1)
untuk Untuk α = + 6, β = -3
6 + (-3) = -(p+1)
3 = -p – 1
p = -4
untuk Untuk α = – 6, β = +3
-6 + 3 = -(p+1)
-3 = -p – 1
p = 2
Karena p ≥ 0, maka yang memenuhi yaitu p = 2
JAWABAN C
Soal No.6
Dina, Ety, dan Feby belanja di loko yang sama. Dina membeli 5 bungkus mie dan 2 kaleng susu kental seharga Rp 25.500,00. Ety membeli 10 bungkus mie dan 3 kaleng susu kental seharga Rp 42.000,00. Jika Feby membeli 1 bungkus mie dan 1 kaleng susu kental. Feby harus membayar sebesar….
- Rp 13.000,00
- Rp 12.000,00
- Rp 10.500,00
- Rp 11.000,00
- Rp 12.500,00
PEMBAHASAN :
misalkan
1 bungkus mie = a
1 kaleng susu = b
maka:
Dina : 5a + 2b = 25.500
Ety: 10a + 3b = 42.000
Feby: a + b = ?
eliminasi a
5a + 2b = 25.500 |x2| 10a + 4b = 51.000
10a + 3b = 42.000 |x1| 10a + 3b = 42.000 ,-
b = 9.000
substitusikan b ke persamaan 5a + 2b = 25.200
5a + 2(9.000) = 25.500
5a + 18.000 = 25.500
5a = 7.500
a = 1.500
maka harga yang harus feby bayar adalah
a + b = 1.500 + 9.000 = 10.500
JAWABAN C
Soal No.7
Persamaan garis singgung pada lingkaran 2x2 +2y2 – 4x +8y – 8 = 0 yang sejajar dengan garis 5x + 12y-15 = 0 adalah….
- 5x + 12y – 20 = 0 dan 5x + 12y+58 = 0
- 5x + 12y – 20 = 0 dan 5x + 12y+20 = 0
- 12x + 5y – 20 = 0 dan 12x + 5y+20 = 0
- 12x + 5y = -20 = 0 dan 5x + 12y = 58
- 5x + 12y = – 20 dan 5x + 12y = 58
PEMBAHASAN :
Menentukan titik pusat lingkaran:
2x2 + 2y2 – 4x + 8y – 8 = 0 (dibagi 2)
menjadi:
x2 + y2 – 2x + 4y – 4 = 0
A = -2, B = 4
Jika bentuk umum: x2 + y2 + Ax + By + C = 0
maka menentukan pusat lingkaran = =
= (1, -2)
Menentukan jari-jari lingkaran:
Menentukan gradien garis 5x + 12y – 15 = 0
5x + 12y – 15 = 0
12y = -5x + 15
maka:
Persamaan Garis Singgung jika lingkaran pusat (x1, y1) dengan jari-jari r dan sejajar ax + by + c = 0 ditentukan dengan rumusan:
5x + 12y = 5(1) + 12(-2) ± 3
5x + 12y + 19 ± 39 = 0
maka dua persamaan garis singgungnya adalah
5x + 12y + 58 = 0 dan 5x + 12y – 20 = 0
JAWABAN A
Soal No.8
PEMBAHASAN :
f(x) = 3x + 4
g(x) = , x ≠ – 1/2
Menentukan invers caranya
, maka
JAWABAN D
Soal No.9
Diketahui premis-premis berikut:
Premis 1 : Jika harga BBM naik, maka harga bahan pokok naik
Premis 2 : Jika harga bahan pokok naik, maka beberapa orang tidak senang
Premis 3 : Semua orang senang
Kesimpulan yang sah dari ketiga premis tersebut adalah….
- Harga BBM naik
- Harga BBM tidak naik
- Harga BBM tidak naik atau beberapa orang tidak senang
- Harga bahan pokok naik dan beberapa orang tidak senang
- Jika harga BBM naik maka beberapa orang tidak senang
PEMBAHASAN :
Jika dimisalkan:
p : harga BBM naik
q : harga bahan pokok naik
r : beberapa orang tidak senang
maka
premis I : p → q
premis II : ∼r
menurut modus tollens
p ⇒ q
∼q
∴ ∼p
maka kesimpulan yang tepat dari harga ketiga premis tersebut adalah harga BBM tidak naik
JAWABAN B
Soal No.10
Suku banyak berderajat 3. jika dibagi (x2 + 2x – 3) bersisa (3x – 4), jika dibagi (x2 – x – 2) bersisa (2x + 3). Suku banyak tersebut adalah….
- x3 – x2 – 2x – 1
- x3 + x2 – 2x – 1
- x3 + x2 + 2x – 1
- x3 + 2x2 – x – 1
- x3 + 2x2 + x + 1
PEMBAHASAN :
Misal: f(x) suku banyak berderajat 3
1. Jika f(x) dibagi (x2 + 2x – 3) bersisa 93x – 4), maka:
f(x) = (x2 + 2x – 3)(ax +b) + (3x – 4)
f(x) = (x+3)(x-1)(ax + b) + (3x – 4)
x = -3 dan x = 1
f(-3) = 3(-3) – 4 = -13
f(1) = 3(1) – 4 = -1
2. Jika f(x) dibagi (X2 – x – 2) bersisa (2x + 3),maka:
f(x) = (x2 – x – 2)(ax +b) + (2x + 3)
f(x) = (x-2)(x+1)(ax + b) + (2x + 3)
untuk f(1) = -1
(-1)(2)(a+b)+(2+3) = -1
-2a – 2b = -6
a+b = 3…(1)
untuk f(-3) = -13
(-5)(-2)(-3a+b)+(2(-3)+3) = -13
-30a + 10b = -10
-3a + b = -1….(2)
Persamaan 1 dan 2 di eliminasi sehingga diperoleh a = 1 dan b = 1
Maka suku banyak tersebut adalah
f(x) = (x2 – x – 2)(ax + b) + (2x + 3)
f(x) = (x2 – x – 2)(x + 2) + (2x + 3)
f(x) = x3 + x2 – 2x – 1
JAWABAN B
Soal No.11
Pernyataan yang ekuivalen dengan pernyataan “Jika semua siswa hadir, maka beberapa guru tidak hadir” adalah….
- Beberapa siswa tidak hadir atau beberapa guru hadir.
- Semua siswa tidak hadir atau beberapa guru tidak hadir.
- Beberapa siswa tidak hadir dan semua guru tidak hadir.
- Beberapa siswa tidak hadir atau beberapa guru tidak hadir.
- Semua siswa hadir dan beberapa guru hadir.
PEMBAHASAN :
Misalkan:
p = semua siswa hadir
q = beberapa guru tidak hadir
Pernyataan tersebut dapat ditulis:
p ⇒ q ≡∼ p v q
Jadi, pernyataan yang setara asalah Beberapa siswa tidak hasir atau beberapa guru tidak hadir
JAWABAN D
DOWNLOAD CONTOH SOAL & PEMBAHASAN SOAL UN MATEMATIKA 2014 DALAM BENTUK PDF Klik Disini
Soal No.12
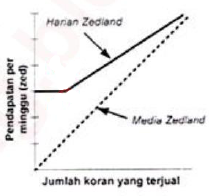
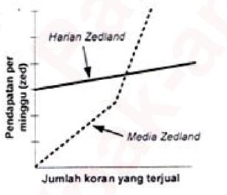
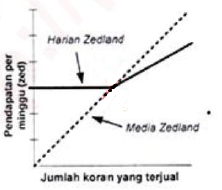
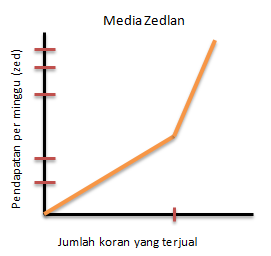
Di Zedland ada dua media massa koran yang sedang mencari orang unluk bekerja sebagai penjual koran. Iklan di bawah ini menunjukkan bagaimana mereka membayar gaji penjual koran.
Joko memutuskan untuk melamar menjadi penjual koran. Ia perlu memilih bekerja pada Media Zedland atau Harian Zedland. Grafik manakah di bawah ini yang menggambarkan bagaimana koran membayar penjual-penjualnya?
PEMBAHASAN :
Jika dimisalkan:
x = banyaknya koran yang terjual per minggu
y = penghasilan per minggu
1. Media Zedland
b. Untuk penjualan di atas 240, persamaannya : y = (0,2 + 0,4)x = 0,6x
Maka grafiknya:
2. Harian Zedland
Maka grafiknya:
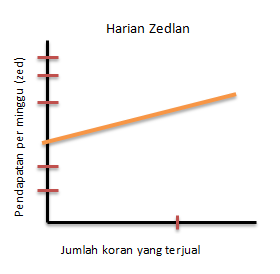
Maka jika digabungkan grafiknya menjadi:
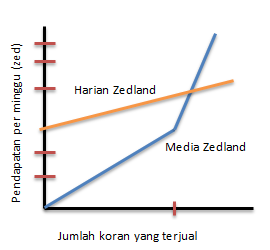
JAWABAN C
Soal No.13
PEMBAHASAN :
Karena vektor a dan b saling tegak lurus maka:
(1)(-1) + (p)(2) + (3)(-3) = 0
-1 + 2p – 9 = 0
2p = 10
p = 5
Sehingga:
JAWABAN C
Soal No.14
- 2
- 4
PEMBAHASAN :
merupakan proyeksi
pada
sehingga
pada
kolinear
p = n.v
- 4 = na
- -bn = -2
- n = n
2b = a
karena a = 2b
Maka:
JAWABAN C
Soal No.15
- -2
- -1
- 1
- 2
PEMBAHASAN :
8 = 6x + 14
6x = -6
x = -1
JAWABAN B
Soal No.16
Penyelesaian pertidaksamaan 3log x.1-2x log 9 > 2 – 1-2xlog 9 adalah….
- 0 < x < 1/5
- 0 < x < 1/2
- 0 < x < 2/5
- 1/5 < x < 1/2
- 2/5 < x < 1/2
Soal No.17
Persamaan bayangan Iingkaran x2 + y2 = 4 bila dicerminkan terhadap garis x = 2 dan dilanjutkan dengan translasi adalah….
- x2 +y2 -2x – 8y + 13 =0
- x2 +y2 +2x – 8y + 13 =0
- x2 +y2 -2x + 8y + 13 =0
- x2 +y2 +2x + 8y + 13 =0
- x2 +y2 +8x – 2y + 13 =0
JAWABAN A
Soal No.18
Himpunan penyelesaian dari 9x – 3x+1 > 54 adalah….
- {x|x> 2, x E R}
- {x|x< -6, x E R}
- {x|x> 4, x E R}
- {x|x< -3, x E R}
- {x|x > 9, x E R}
PEMBAHASAN :
JAWABAN A
Soal No.19
Seutas tali dipotong menjadi 5 bagian sehingga panjang potongan-potongan tali tersebut membentuk barisan geometri. Jika panjang tali terpendek 6 cm dan potongan tali terpanjang 96 cm, maka panjang tali semula adalah…
- 96 cm
- 185 cm
- 186 cm
- 191 cm
- 192 cm
PEMBAHASAN :
JAWABAN C
Soal No.20
Tempat duduk gedung pertunjukan film diatur mulai dari baris depan ke belakang dengan banyak baris di belakang lebih 4 kursi dari baris di depannya. Bila dalam gedung pertunjukan terdapat 15 baris kursi dan baris terdepan ada 20 kursi. kapasitas gedung pertunjukan tersebut adalah….
- 1200 kursi
- 800 kursi
- 720 kursi
- 600 kursi
- 300 kursi
Soal No.21
PEMBAHASAN :
JAWABAN C
Soal No.22
Diketahui matriks . Jika BT adalah transpose dari matriks B, A + BT – C =
, maka nilai w + x + y + z adalah….
- 8
- 9
- 11
- 14
- 17
Soal No.23
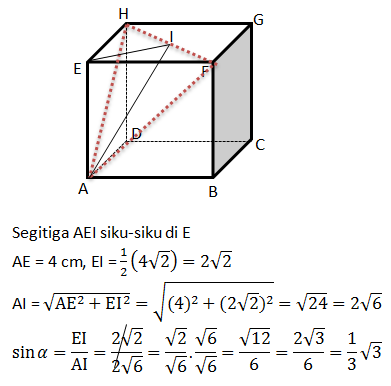
Diketahui kubus ABCD.EFGH dengan rusuk 9 cm, Jika titik T terletak pada pertengahan garis HF, Jarak titik A ke garis CT adalah….
Soal No.24
Nilai adalah….
- 5
- 4
- 3
- 2
- 1
PEMBAHASAN :
JAWABAN D
Soal No.25
- 16
- 12
- 8
- 4
- 2
Soal No.26
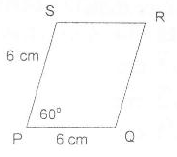
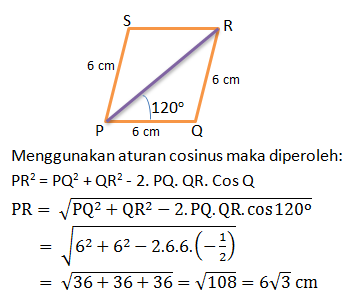
Diketahui jajargenjang PQRS seperti gambar.
cm
cm
cm
cm
- 8 cm
Soal No.27
Nilai dari cos 145o + cos 35o – cos 45o =
PEMBAHASAN :
JAWABAN E
Soal No.28
Himpunan penyelesaian dari persamaan 2 cos 3xo = 1. untuk 0 ≤ x ≤ 180, adalah…
- {0, 20, 60}
- {0, 20, 100}
- {20, 60, 100}
- {20, 100, 140}
- {100, 140, 180}
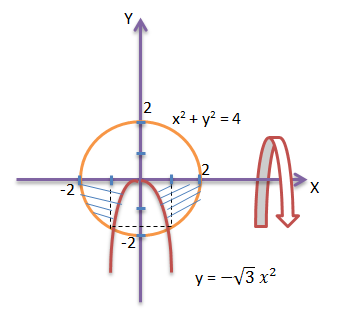
Soal No.29
Soal No.30
Soal No.31
Soal No.32
Soal No.33
Diketahui g(x) = 1/3 x3 – A 2x + 1; f(x) = g(2x-1), A suatu konstanta. Jika f naik pada x ≤ 0 atau x ≥ 1, nilai maksimum relatif g adalah….
Soal No.34
satuan volume
satuan volume
satuan volume
satuan volume
satuan volume
Soal No.35
PEMBAHASAN :
JAWABAN E
Soal No.36
Dua dadu dilempar undi bersama satu kali. Peluang muncul jumlah kedua mata dadu 4 atau 7 adalah…
PEMBAHASAN :
JAWABAN E
Soal No.37
Pada suatu tes penerimaan pegawai, seorang pelamar wajib mengerjakan 6 soal diantara 14 soal. Soal nomor 1 sampai 3 harus dikerjakan. Banyak pilihan soal yang dapal dilakukan adalah….
- 2.002 cara
- 990 cara
- 336 cara
- 165 cara
- 120 cara
Soal No.38
- 49.25
- 48,75
- 48,25
- 47,75
- 47,25
Soal No.39
- 23,25
- 23,75
- 24,00
- 25,75
- 26,25
Soal No.40
Joni mempunyai koleksi 3 pasang sepatu dengan merk yang berbeda, 4 baju berlainan coraknya, dan 3 celana yang berbeda warna. Banyak cara berpakaian Joni dengan penampilan yang berbeda adalah….
- 36
- 24
- 21
- 12
- 10
PEMBAHASAN :
Banyak cara berpakaian joni yaitu mengalikan ke semua variasi merk sepatu, corak baju dan warna celana
banyak cara = 3 x 4 x 3 = 36 cara
JAWABAN A
BINGUNG ADA YANG BELUM JELAS?
ADA YANG MAU DITANYAKAN?
MASUK KESINI : TEMPAT NANYA
UNTUK BERTANYA DAN BERBAGI ILMU BERSAMA
Semoga Bermanfaat