Pembahasan Matematika SMP UN 2018 No. 6

Pembahasan soal Matematika SMP Ujian Nasional (UN) tahun 2018 nomor 6 sampai dengan nomor 10 tentang:

• bentuk akar, 
• pola bilangan, 
• suku ke-n barisan aritmetika, 
• jumlah n suku barisan aritmetika, dan 
• aritmetika sosial [untung-rugi].

Soal No. 6 tentang Bentuk Akar

Bentuk sederhana dari

adalah ….

A.   2√12
B.   5√4
C.   6√10
D.   2√3

Pembahasan

Kita sederhanakan bilangan-bilangan yang diakar.

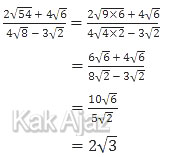
Jadi, bentuk sederhana dari bentuk akar tersebut adalah 2√3 (D).

Perdalam materi ini di Operasi Bilangan Bentuk Akar [Soal UN dan Pembahasan].

Soal No. 7 tentang Pola Bilangan

Pembahasan

Barisan di atas mempunyai selisih yang selalu bertambah secara tetap.

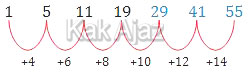
Jadi, tiga suku berikutnya dari barisan tersebut adalah 29, 41, 55 (B).

Soal No. 8 tentang Suku ke-n Barisan Aritmetika

Perhatikan pola berikut ini!

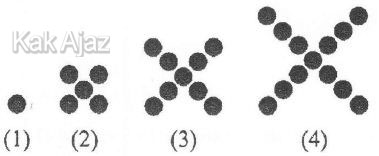
Jika pola di atas dilanjutkan, banyak bulatan pada pola ke-61 adalah ….

A.   249
B.   241
C.   66
D.   64

Pembahasan

Banyak bulatan pada setiap pola di atas adalah:

1, 5, 9, 13, …

Ternyata pola di atas membentuk barisan aritmetika dengan:

a = 1
b = 4

Suku ke-n barisan aritmetika dirumuskan:

 U_n = a + (n − 1)b
U₆₁ = 1 + (61 − 1)×4
       = 1 + 60×4
       = 1 + 240
       = 241

Jadi, banyak bulatan pada pola ke-61 adalah 241 (B).

Soal No. 9 tentang Jumlah n Suku Barisan Aritmetika

Pembahasan

Yang merupakan kelipatan 3 dan 4 adalah kelipatan 12. Bilangan kelipatan 12 antara 200 dan 450 adalah:

204, 216, 228, …, 444.

Bilangan-bilangan tersebut membentuk barisan aritmetika dengan:

  a = 204
  b = 12
U_n = 444

Suku terakhirnya U_n = 444. Mari kita cari, ada berapa banyak suku barisan tersebut.

                      U_n = 444
        a + (n − 1)b = 444
204 + (n − 1)×12 = 444
   204 + 12n − 12 = 444
           12n + 192 = 444
                      12n = 252
                          n = 21

Jumlah semua suku barisan tersebut dapat dicari dengan rumus:

 S_n = 1/2 n(a + U_n)
S₂₁ = 1/2 ×21(204 + 444)
      = 21/2 × 648
      = 6804

Jadi, jumlah semua bilangan kelipatan 3 dan 4 antara 200 dan 450 adalah 6.804 (B).

Soal No. 10 tentang Aritmetika Sosial [untung-rugi]

Pembahasan

Untung 25% berarti harga jualnya (100+25)%.

Jadi, harga jual televisi tersebut adalah Rp4.500.000,00 (D).

Simak Pembahasan Soal Matematika SMP UN 2018 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih