pembahasan selanjutnya adalah

Pembahasan soal Matematika SMP Ujian Nasional (UN) tahun 2018 nomor 16 sampai dengan nomor 20 tentang:
- persamaan linear,
- penerapan persamaan linear,
- himpunan bagian,
- operasi himpunan, dan
- diagram Venn.
Soal No. 16 tentang Persamaan Linear
2(3x − 5) + 3 = 3(4x + 2) − 1
maka nilai 3k + 5 sama dengan ….
A. 2
B. 1
C. −1
D. −2
Pembahasan
Kita buka dulu kurungnya kemudian yang mengandung variabel x diletakkan di sebelah kiri.
| 2(3x − 5) + 3 | = | 3(4x + 2) − 1 |
| 6x − 10 + 3 | = | 12x + 6 − 1 |
| 6x − 7 | = | 12x + 5 |
| 6x − 12x | = | 5 + 7 |
| −6x | = | 12 |
| x | = | −2 |
Nilai x = −2 ini sama dengan nilai k sehingga
3k + 5 = 3×(−2) + 5
= −6 + 5
= −1
Jadi, nilai 3k + 5 sama dengan −1 (C).
Soal No. 17 tentang Penerapan Persamaan Linear
A. p > 50
B. p ≥ 50
C. p > 90
D. p ≥ 90
Pembahasan
Keliling taman tidak kurang dari 140 meter.
| K | ≥ | 140 |
| 2(p + l) | ≥ | 140 |
| p + l | ≥ | 70 |
| 8x + 2 + 6x − 16 | ≥ | 70 |
| 14x − 14 | ≥ | 70 |
| 14x | ≥ | 84 |
| x | ≥ | 6 |
Dengan demikian, panjang taman tersebut adalah:
p = 8x + 2
p ≥ 8×6 + 2
p ≥ 48 + 2
p ≥ 50
Jadi, panjang taman tersebut adalah p ≥ 50 (B).
Soal No. 18 tentang Himpunan Bagian
K = {1 < x ≤ 11, x bilangan ganjil}.
Banyak himpunan bagian dari himpunan K yang mempunyai 3 anggota adalah ….
A. 4
B. 10
C. 20
D. 35

Pembahasan
Himpunan K himpunan bilangan ganjil antara 1 sampai dengan 11.
Himpunan bagian dari K yang mempunyai 3 anggota dapat ditentukan dengan segitiga pascal sebagai berikut:
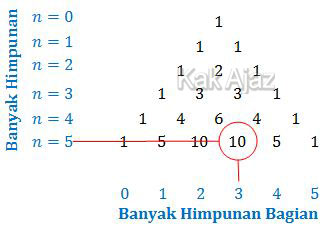
Jadi, banyak himpunan bagian dari himpunan K yang mempunyai 3 anggota adalah 10 (B).
Soal No. 19 tentang Operasi Himpunan
A adalah himpunan bilangan prima antara 3 dan 20.
B adalah himpunan bilangan asli antara 2 dan 15.
Komplemen A ∩ B adalah ….
| A. | {0, 1, 2, 5, 7, 11. 13. 15, 16, 18} |
| B. | {3, 4, 6, 8, 9, 10, 12, 14, 17, 19} |
| C. | {3, 4, 6, 8, 9, 10, 12, 14, 15, 17, 19} |
| D. | {0, 1, 2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 17, 18, 19} |
Pembahasan
Anggota himpunan S, A, dan B adalah:
| S | = | {0, 1, 2, 3, …, 20} |
| A | = | {5, 7, 11, 13, 17, 19} |
| B | = | {3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} |
A ∩ B (baca: himpunan A irisan B) adalah anggota himpunan A yang juga anggota himpunan B.
A ∩ B = {5, 7, 11, 13}
Komplemen A ∩ B adalah selain anggota himpunan A ∩ B tetapi masih dalam himpunan semesta.
| (A ∩ B)c | = | {0, 1, 2, 3, 4, 6, 8, 9, 10, 12, 14, 15, 16, 17, 18, 19} |
Jadi, komplemen A ∩ B adalah opsi (D).
Soal No. 20 tentang Diagram Venn
A. 8 orang
B. 10 orang
C. 12 orang
D. 14 orang
Pembahasan
Soal di atas lebih efektif dikerjakan dengan diagram Venn. Pengisiannya harus dimulai dari irisan.
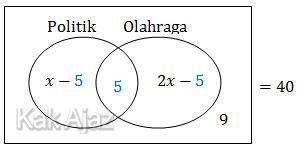
Misal yang menyukai makalah politik adalah x maka yang menyukai majalah olahraga adalah 2x. Masing-masing dikurangi 5 karena 5 orang sudah masuk dalam irisan.
Ok, mari kita hitung!
| x − 5 + 5 + 2x − 5 + 9 | = | 40 |
| 3x + 4 | = | 40 |
| 3x | = | 36 |
| x | = | 12 |
Jadi, banyak pembaca yang menyukai majalah politik adalah 12 orang (C).
Simak Pembahasan Soal Matematika SMP UN 2018 selengkapnya.
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat