Pembahasan Matematika SMP UN 2016 No. 21

• grafik fungsi kuadrat, 
• sistem persamaan linear, 
• garis dan sudut, serta 
• sifat segitiga.

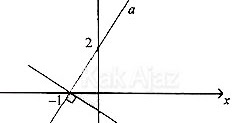
Soal No. 21 tentang Grafik Fungsi Garis Lurus

Persamaan garis b seperti tampak pada gambar adalah ….

A.   2y = x − 1
B.   2y = −x − 1
C.   2y = x + 1
D.   2y = −x + 1

Pembahasan

Garis a melalui titik (−1, 0) dan (0, 2). Gradien garis a adalah:

m_a = ∆y/∆x
      = (2 − 0)/(0 − (−1))
      = 2

Garis b tegak lurus garis a. Dua garis yang saling tegak lurus, perkalian gradiennya sama dengan −1.

m_a × m_b = −1
   2 × m_b = −1
         m_b = −1/2

Garis b melalui titik (−1,0) dengan gradien −1/2 adalah:

y − y₁ = m(x − y₁)
 y − 0 = −1/2 (x + 1)

Masing-masing suku kalikan dengan 2, diperoleh:

2y = −x − 1

Jadi, persamaan garis b adalah 2y = −x − 1 (B).

Soal No 22 tentang Sistem Persamaan Linear

Pembahasan

Kita misalkan terlebih dahulu.

x : mobil
y : motor

Model matematika untuk soal di atas adalah:

3x + 5y = 17.000 … (1)

4x + 2y = 18.000
2x + y = 9.000     … (2)

Sekarang kita eliminasi 2 persamaan tersebut.

  2x + y = 9.000   |×5| 10x + 5y = 45.000
3x + 5y = 17.000 |×1|   3x + 5y = 17.000
                                 ⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  −
                                             7x = 28.000
                                               x = 4.000

Substitusi x = 4.000 ke persamaan (2).

         2x + y = 9.000
2×4.000 + y = 9.000
    8.000 + y = 9.000
                 y = 1.000

Jika terdapat 20 mobil dan 30 motor, banyak uang parkir yang ia peroleh adalah:

20x + 30y = 20×4.000 + 30×1.000
                 = 80.000 + 30.000
                 = 110.000

Jadi, banyak uang parkir yang ia peroleh adalah Rp110.000,00 (C).

Soal No. 23 tentang Garis dan Sudut

Perhatikan gambar berikut!

Besar pelurus sudut KLN adalah ….

A.   31°
B.   72°
C.   85°
D.   155°

Pembahasan

Hati-hati dengan soal di atas, yang ditanyakan bukan sudut KLN, tetapi pelurus sudut KLN, yaitu sudut MLN.

Karena kedua sudut saling berpelurus maka jumlah keduanya adalah 180°.

          ∠KLN + ∠MLN = 180°
(3x + 15)° + (2x + 10)° = 180°
                       5x + 25° = 180°
                                 5x = 155°
                                   x = 31°

Dengan demikian, pelurus ∠KLN adalah:

pelurus ∠KLN = ∠MLN
                        = 2x + 10°
                        = 2×31° + 10°
                        = 62° + 10°
                        = 72°

Jadi, pelurus sudut KLM adalah 72° (B).

Soal No. 24 tentang Garis dan Sudut

Perhatikan gambar!

Besar sudut BAC adalah ….

A.   30°
B.   40°
C.   50°
D.   90°

Pembahasan

Sudut ABC berpelurus dengan sudut CBD sehingga:

∠ABC + ∠CBD = 180°
   ∠ABC + 140° = 180°
               ∠ABC = 40°

Sementara itu, jumlah sudut-sudut segitiga sama dengan 180°.

             ∠A + ∠B + ∠C = 180°
y + 10° + 40° + 2y +10° = 180°
                         3y + 60° = 180°
                                   3y = 120°
                                     y = 40°

Nah, sekarang masuk ke pertanyaan.

∠BAC = y + 10°
            = 40° + 10°
            = 50°

Jadi, Besar sudut BAC adalah 50° (C).

Soal No. 25 tentang Sifat Segitiga

Pembahasan

Syarat terbentuknya segitiga adalah sisi terpanjang harus lebih kecil dari jumlah dua sisi lainnya.

Jika panjang sisi-sisi sebuah segitiga adalah p, q, dan r, dengan p > q > r (p sisi terpanjang) maka berlaku:

q + r > p

Bentuk di atas tidak terdapat pada opsi jawaban. Mari kita pindah ruas!

q − p > −r

Masih tidak ada. Sekarang masing-masing suku dikalikan negatif (tanda pertidaksamaan akan berubah)

−q + p < r
  p − q < r
 
Nah, ada kan?

Jadi, pernyataan yang benar untuk segitiga tersebut adalah opsi (C).

Simak Pembahasan Soal Matematika SMP UN 2016 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih