Pembahasan Matematika SMP UN 2015 No. 21

By Posted on

pembahasan selanjutnya adalah

Pembahasan soal Matematika SMP Ujian Nasional tahun 2015 nomor 21 sampai dengan nomor 25 tentang:
  • teorema Pythagoras, 
  • luas bangun datar, 
  • penerapan luas bangun datar, 
  • penerapan keliling bangun datar, serta 
  • kesebangunan.

Soal No. 21 tentang Teorema Pythagoras

Sebuah tiang tingginya 12 m berdiri tegak di atas tanah datar. Dari ujung atas tiang ditarik seutas tali ke sebuah patok pada tanah. Jika panjang tali 15 m, jarak patok dengan pangkal tiang bagian bawah adalah ….

A.   13,5 m
B.   10 m
C.   9 m
D.   3 m



Pembahasan

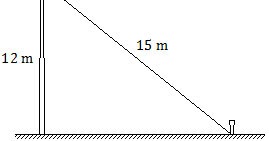
Soal di atas dapat digambarkan sebagai berikut:

Tiang yang ditarik dengan tali membentuk segitiga pythagoras

Ilustrasi gambar di atas membentuk segitiga siku-siku sehingga berlaku teorema Pythagoras.


   
    = √81
    = 9

Jadi, jarak antara patok dengan kaki tiang adalah 9 m (C).

Soal No. 22 tentang Luas Bangun Datar

Perhatikan gambar!
Luas belah ketupat dan jajargenjang

Jika panjang OE = 6 cm maka luas ABCDEF adalah ….

A.   232 cm2
B.   256 cm2
C.   304 cm2
D.   400 cm2

Pembahasan

Bangun di atas terdiri dari belah ketupat dan jajargenjang. Mari kita tinjau satu per satu.

Diagonal belah ketupat:

OE = 6 cm 
d1 = AE
     = 2 × OE
     = 2 × 6 cm
     = 12 cm

BE = CD = 10 cm

       
        = √64
        = 8 cm 

d2 = BF
     = 2 × OB
     = 2 × 8 cm
     = 16 cm

Luas belah ketupat: 

LI = ½ × d1 × d2
    = ½ × 12 × 16 cm2
    = 96 cm2

Jajargenjang

alas jajargenjang    : a = BC = ED = 20 cm
tinggi jajargenjang : t = OB = 8 cm

Luas jajargenjang: 

LII = a × t
      = 20 × 8 cm2
      = 160 cm2

Dengan demikian, luas seluruh bangun tersebut adalah: 

L= LI + LII
   = (96 + 160) cm2
   = 256 cm2

Artkel Terkait  Pembahasan Matematika IPS UN 2014 No. 16

Jadi, luas bangun ABCDEF adalah 256 cm2 (B).

Soal No. 23 tentang Penerapan Luas Bangun Datar

Sebuah kolam renang berbentuk persegi panjang berukuran panjang 15 m dan lebar 10 m. Di sekeliling kolam akan dibuat jalan dengan lebar 2 m dan dipasang keramik. Luas keramik untuk jalan tersebut adalah ….

A.   116 m2
B.   100 m2
C.   58 m2
D.   50 m2



Pembahasan

Perhatikan gambar ilustrasi soal di atas berikut ini!

Keramik di sekeliling kolam

Berdasarkan gambar di atas, luas keramik di sekeliling kolam merupakan luas tepi luar kolam dikurangi luas kolam.

Luas keramik = 19 × 14 − 15 × 10
                      = 266 − 150
                      = 116

Jadi, luas keramik untuk jalan di sekeliling kolam adalah 116 m2 (A).

Soal No. 24 tentang Penerapan Keliling Bangun Datar 

Sebuah taman berbentuk persegi panjang berukuran panjang 32 m dan lebar 24 m. Di sekeliling taman akan dipasang lampu dengan jarak antarlampu 4 m. Jumlah lampu yang diperlukan sebanyak ….

A.   14 lampu
B.   28 lampu
C.   52 lampu
D.   112 lampu

Pembahasan

Keliling taman tersebut adalah: 

K = 2(p + l)
    = 2 × (32 + 24)
    = 2 × 56
    = 112

Di sepanjang 112 m tersebut akan dipasang lampu dengan jarak antarlampu 4 m. Banyak lampu yang diperlukan adalah:

Banyak lampu = 112 : 4
                       = 28

Jadi, jumlah lampu yang diperlukan di sekeliling taman tersebut adalah 28 lampu (B).

Soal No. 25 tentang Kesebangunan

Perhatikan gambar!
Trapesium sebangun

Trapesium ABFE sebangun dengan trapesium EFCD. Jika CF : FB = 2 : 3 maka panjang CD adalah ….

A.   6 cm
B.   9 cm
C.   12 cm
D.   15 cm

Pembahasan

Agar lebih mudah dipahami, dua trapesium sebangun tersebut kita pisahkan.

Artkel Terkait  Try Out (TO) SBMPTN SAINTEK Tahun 2014 Dengan Jawaban

Dua trapesium sebangun

Berdasarkan gambar di atas, diperoleh perbandingan antara trapesium kecil dan besar sebagai berikut:



3EF = 54
  EF = 18

 
 
3 CD = 36
   CD = 12

Jadi, panjang CD adalah 12 cm (C).

Simak Pembahasan Soal Matematika SMP UN 2015 selengkapnya.

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih

Semoga Bermanfaat

Related posts:

Leave a Reply

Your email address will not be published. Required fields are marked *