Pembahasan Matematika SMP UN 2014 No. 16 My Brain

pembahasan selanjutnya adalah

Pembahasan soal Matematika SMP Ujian Nasional 2014 nomor 16 sampai dengan nomor 20 tentang:

grafik fungsi linear,
persamaan garis lurus,
gradien garis lurus,
sistem persamaan linear dua variabel, serta
aplikasi sistem persamaan linear dua variabel.

Soal No. 16 tentang Grafik Fungsi Linear

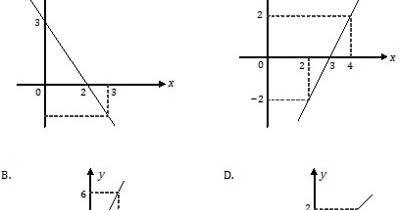
Grafik fungsi f(x) = 2x + 2 dengan x ∈ R adalah ….

Grafik fungsi f(x) = 2x + 2, linear, garis

Pembahasan

Bentuk umum persamaan garis pada soal di atas adalah

y = mx + c

dengan m adalah gradien (kemiringan) dan c adalah ordinat titik potong pada sumbu y.

Ketentuan untuk nilai m adalah sebagai berikut:

m = ⊕ : garis miring ke kanan ( / )
m = ⊖ : garis miring ke kiri ( \ )

Mari kita padukan persamaan garis di atas dengan bentuk umumnya.

f(x) = 2x + 2
y = mx + c

Berdasarkan bentuk umum tersebut diperoleh m = 2 (positif) berarti garisnya miring ke kanan serta c = 2 berarti memotong sumbu y di (0, 2).

Jadi, grafik fungsi tersebut yang sesuai adalah opsi (B).

Soal No. 16 dari Paket Soal yang Lain

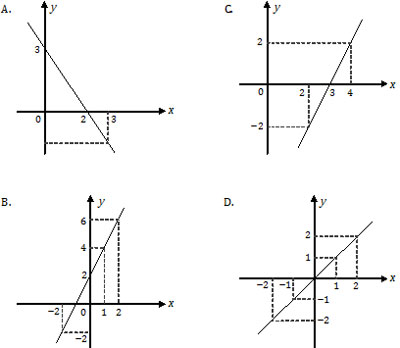
Grafik fungsi yang menyatakan f(x) = 3x − 2, x ∈ R adalah ….

Jawab:

c = −2 : memotong sumbu y di (0, −2)
m = +3 : garis miring ke kanan (A).

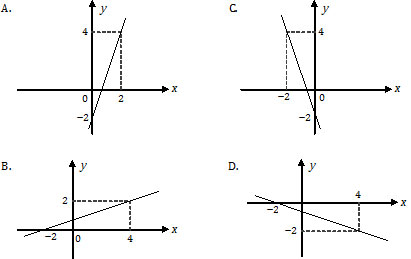
Grafik fungsi yang tepat untuk f(x) = 5 − 3x, untuk x ∈ Real adalah ….

Jawab:

c = 5 : memotong sumbu y di (0, 5)
m = −3 : garis miring ke kiri (B).

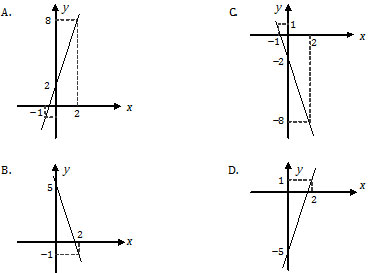
Grafik fungsi dari f(x) = 6 − 2x dengan x ∈ R adalah ….

Jawab:

c = 6 : memotong sumbu y di (0, 6)
m = −2 : garis miring ke kiri (A).

Grafik fungsi dari f(x) = x − 1 dengan x ∈ R adalah ….

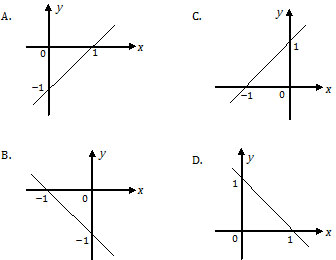
Jawab:

c = −1 : memotong sumbu y di (0, −1)
m = +1 : garis miring ke kanan (A).

Gambar grafik Kartesius yang menyatakan f(x) = 2x − 1, x ∈ R adalah ….

Jawab:

c = −1 : memotong sumbu y di (0, −1)
m = +2 : garis miring ke kanan (A).

Grafik fungsi dari f(x) = −2x dengan domain dan kodomainnya bilangan real adalah ….

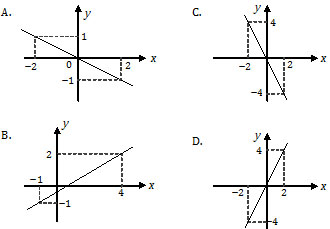
Jawab:

c = 0 : memotong sumbu y di (0, 0) atau melalui pangkal koordinat
m = −2 : garis miring ke kiri.

Ada dua opsi yang memotong pangkal koordinat dan miring ke kiri, yaitu (A) dan (C). Mari kita uji dengan memasukkan x = 2 pada f(x).

f(x) = −2x
f(2) = −2×2
y = −4

Jadi, grafik fungsi tersebut juga melalui titik (2, −4) (C).

Soal No. 17 tentang Persamaan Garis Lurus

Persamaan garis berikut yang tegak lurus dengan garis yang melalui titik (−1, 7) dan (0, 2) adalah ….

A. 5x − y = −23
B. x − 5y = 37
C. x + 5y = −37
D. 5x + y = 11

Pembahasan

Gradien garis yang melalui titik (−1, 7) dan (0, 2) adalah

$m_{1}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$
$=\frac{2-7}{0-(-1)}$
= −5

Karena kedua garis saling tegak lurus, berlaku

m₁ . m₂ = −1
−5 . m₂ = −1
m₂ = 1/5

m₂ adalah gradien garis pada opsi jawaban.

Persamaan garis pada opsi jawaban berbentuk ax + by = c. Rumus gradien untuk bentuk tersebut adalah

$m_{2}=-\frac{a}{b}$

Nah, dengan menggunakan rumus tersebut, mari kita periksa setiap opsi jawaban, mana yang mempunyai gradien 1/5.

A.   5x − y = −23     m₂ = 5
B. x − 5y = 37       m₂ = 1/5
C. x + 5y = −37     m₂ = −1/5
D. 5x + y = 11       m₂ = −5

Jadi, persamaan garis yang dimaksud adalah opsi (B).

Soal No. 17 dari Paket Soal yang Lain

Persamaan garis di bawah yang tegak lurus dengan garis yang melalui titik P(−3, 8) dan Q(2, 5) adalah ….

A. 3x − 5y − 14 = 0
B. 3x + 5y + 14 = 0
C. 5x + 3y − 42 = 0
D. 5x − 3y − 42 = 0

Jawab:

$m_{1}=\frac{5-8}{2-(-3)}=-\frac{3}{5}$

⊥ : m₁ . m₂ = −1
−3/5 . m₂ = −1
m₂ = 5/3

Dengan menggunakan rumus m₂ = −a/b, opsi jawaban yang mempunyai m₂ = 5/3 adalah opsi (D).

Persamaan garis yang tegak lurus dengan garis yang melalui titik A(2, −2) dan B(−4, 1) adalah ….

A. y = 2x − 3
B. y = 1/2 x − 6
C. y = −1/2 x + 6
D. y = −2x + 6

Jawab:

$m_{1}=\frac{1-(-2)}{-4-2}=-\frac{1}{2}$

⊥ : m₁ . m₂ = −1
−1/2 . m₂ = −1
m₂ = 2

Persamaan garis pada opsi jawaban bentuknya y = mx + c. Nilai m = 2 terlihat jelas pada opsi (A).

Persamaan garis yang tegak lurus dengan garis yang melalui titik (3, 2) dan (−1, 4) adalah ….

Artkel Terkait Allah Swt. sendirilah yang mengetahui kapan terjadinya hari kiamat, mengetahui apa yang terkandung di dalam rahim, mengetahui kapan akan turun hujan. Allah Swt. Maha Mengetahui merupakan makna dari

A.   y = 2x − 1
B.   y = −2x + 7
C.   y = 1/2 x + 2
D.   y = −1/2 x + 4

Jawab:

$m_{1}=\frac{4-2}{-1-3}=-\frac{1}{2}$

⊥ : m₁ . m₂ = −1
−1/2 . m₂ = −1
m₂ = 2

Nilai m = 2 terdapat pada opsi (A).

Persamaan garis yang sejajar dengan garis yang melalui titik A(2, 2) dan B(4, 8) adalah ….

A. y − 3x = −12
B. y + 3x = 18
C. 3x + y = 12
D. x − 3y = 18

Jawab:

$m_{1}=\frac{8-2}{4-2}=3$

Karena kedua garis sejajar maka m₁ = m₂ = 3.

Dengan menggunakan rumus m₂ = −a/b, opsi jawaban yang mempunyai m₂ = 3 adalah opsi (A).

Persamaan garis yang sejajar dengan garis yang melalui titik (−6, 0) dan (3, 3) adalah ….

A.   y = 3x − 13
B.   y = 1/3 x + 2
C.   y = −1/3 x + 7
D.   y = −3x + 23

Jawab:

$m_{1}=\frac{3-0}{3-(-6))}=\frac{1}{3}$

// : m₁ = m₂ = 1/3.

Persamaan garis pada opsi jawaban bentuknya y = mx + c. Nilai m = 1/3 terlihat jelas pada opsi (B).

Persamaan garis yang sejajar dengan garis yang melalui titik (2, 5) dan (−1, −4) adalah ….

A. y = −3x + 4
B. y = −1/3 x + 6
C. y = 1/3 x + 4
D. y = 3x − 4

Jawab:

$m_{1}=\frac{-4-5}{-1-2}=3$

// : m₁ = m₂ = 3.

Nilai m = 3 terdapat pada opsi (D).

Soal No. 18 tentang Gradien Garis Lurus

Titik A(10, p) terletak pada garis yang melalui titik B(3, 1) dan C(−4, −13). Nilai p adalah ….

A. 35
B. 15
C. −5
D. −15

Pembahasan

Karena titik A terletak pada garis yang melalui titik B dan C, berarti ketiga titik tersebut terletak pada satu garis sehingga garis AB dan BC mempunyai gradien yang sama.

m_AB = m_BC
$\frac{1-p}{3-10}=\frac{-13-1}{-4-3}$
$\frac{1-p}{-7}=\frac{-14}{-7}$
1 − p = −14
−p = −15
p = 15

Jadi, nilai p adalah 15 (B).

Soal No. 18 dari Paket Soal yang Lain

Diketahui titik P(1, 5), Q(−2, −1), dan R(3, a). Jika titik P, Q, dan R terletak pada satu garis lurus maka nilai a adalah ….

A. −9
B. −8
C. 8
D. 9

Jawab:

m_PQ = m_QR
$\frac{-1-5}{-2-1}=\frac{a-(-1)}{3-(-2)}$
    $\frac{-6}{-3}=\frac{a+1}{5}$
     10 = a + 1
       a = 9 (D)

Diketahui titik A(1, 2), B(2, 0), dan C(3, p) terletak pada satu garis lurus. Nilai p adalah ….

A. −2
B. −1
C. 1
D. 2

Jawab:

m_AB = m_BC
$\frac{0-2}{2-1}=\frac{p-0}{3-2}$
$\frac{-2}{1}=\frac{p}{1}$
p = −2 (A).

Titik R(−3, k) terletak pada garis yang melalui titik S(4, 7) dan T(2, −1). Nilai k adalah ….

A. −21
B. −19
C. −18
D. 3

Jawab:

     m_RS = m_ST
$\frac{7-k}{4-(-3)}=\frac{-1-7}{2-4}$
     $\frac{7-k}{7}=\frac{-8}{-2}$
    7 − k = 28
        −k = 21
          k = −21 (A).

Sebuah titik P(3, d) terletak pada garis yang melalui titik Q(−2, 10) dan R(1, 1) jika nilai d adalah ….

A. 13
B. 7
C. −5
D. −13

Jawab:

   m_PQ = m_QR
$\frac{10-d}{-2-3}=\frac{1-10}{1-(-2)}$
$\frac{10-d}{-5}=\frac{-9}{3}$
10 − d = 15
      −d = 5
        d = −5 (C).

Diketahui titik A(2, 7), B(−3, −3), dan C(3, a). Jika titik A, B, dan C terletak pada satu garis lurus maka nilai a adalah ….

A.   8
B.   9
C.   11
D.   12

Jawab:

m_AB = m_BC
$\frac{-3-7}{-3-2}=\frac{a-(-3)}{3-(-3)}$
   $\frac{-10}{-5}=\frac{a+3}{6}$
      12 = a + 3
        a = 9 (B).

Diketahui titik K(−2, 3), L(1, −3), dan M(4, a). Jika titik K, L, dan M terletak pada satu garis lurus maka nilai a adalah ….

A. −7
B. −8
C. −9
D. −10

Jawab:

     m_KL = m_LM
$\frac{-3-3}{1-(-2)}=\frac{a-(-3)}{4-1}$
       $\frac{-6}{3}=\frac{a+3}{3}$
        −6 = a + 3
          a = −9 (C).

Soal No. 19 tentang Sistem Persamaan Linear Dua Variabel

Diketahui sistem persamaan x − 3y − 5 = 0 dan 2x − 5y = 9. Nilai dari 3x + 2y adalah ….

A. −1
B. 1
C. 3
D. 4

Pembahasan

Sistem persamaan tersebut dapat diselesaikan dengan cara mengeliminasi kedua persamaan.

x − 3y = 5 |×2|   2x − 6y = 10
2x − 5y = 9 |×1|   2x − 5y =   9
                            —————— −
                                       −y = 1
                                         y = −1

Kemudian substitusi y = −1 ke salah satu persamaan, misal persamaan pertama.

       x − 3y = 5
x − 3×(−1) = 5
         x + 3 = 5
                x = 2

Nah, sekarang substitusi x = 2 dan y = −1 pada pertanyaan.

3x + 2y = 3×2 + 2×(−1)
= 6 − 2
= 4

Jadi, nilai 3x + 2y adalah 4 (D).

Soal No. 19 dari Paket Soal yang Lain

Penyelesaian dari sistem persamaan 2x − 5y = 18 dan 5x − 3y = 26 adalah x dan y. Nilai 4x − 7y adalah ….

Artkel Terkait Pembahasan Matematika IPA UN 2016 No. 11

A. −36
B. −2
C. 2
D. 30

Jawab:

2x − 5y = 18 |×5|   10x − 25y = 90
5x − 3y = 26 |×2|   10x −   6y = 52
                            ——————— −
                                       −19y = 38
                                           y = −2

y = −2 → 2x − 5y = 18
                2x − 5×(−2) = 18
                2x + 10 = 18
                2x = 8
                x = 4

∴ 4x − 7y = 4×4 − 7×(−2)
= 16 + 14 = 30 (D).

Diketahui sistem persamaan linear 3x + 4y = 17 dan 4x − 2y = 8. Nilai dari 2x + 3y adalah ….

A. 13
B. 12
C. 10
D. 8

Jawab:

3x + 4y = 17 |×1|   3x + 4y = 17
4x − 2y =   8 |×2|   8x − 4y = 16
                            ——————— +
                                     11x = 33
                                           x = 3

x = 3 → 4x − 2y = 8
          4×3 − 2y = 8
              12 − 2y = 8
              −2y = −4
              y = 2

∴ 2x + 3y = 2×3 + 3×2
= 6 + 6 = 12 (B).

Diketahui sistem persamaan 4x − 3y = 1 dan 2x − y = −3. Nilai dari 3x − 2y adalah ….

A. −2
B. −1
C. 1
D. 2

Jawab:

4x − 3y =   1 |×1|   4x − 3y =   1
2x −   y = −3 |×2|   4x − 2y = −6
                            —————— −
                                       −y = 7
                                           y = −7

y = −7 → 2x − y = −3
                2x − (−7) = −3
                2x + 7 = −3
                2x = −10
                x = −5

∴ 3x − 2y = 3×(−5) − 2×(−7)
= −15 + 14 = −1 (B).

Diketahui sistem persamaan 4x + 3y = 23 dan 5x − 7y = −25. Nilai dari −3x + 6y adalah ….

A. −24
B. −23
C. 24
D. 36

Jawab:

4x + 3y =   23    |×5|   20x + 15y =   115
5x − 7y = −25 |×4|   20x − 28y = −100
                         ————————— −
                                              43y = 215
                                          y = 5

y = 5 → 4x + 3y = 23
              4x + 3×5 = 23
              4x + 15 = 23
              4x = 8
                x = 2

∴ −3x + 6y = −3×2 + 6×5
= −6 + 30 = 24 (C).

Penyelesaian dari sistem persamaan 2x − 5y = −16 dan 5x + 2y = −11 adalah x dan y. Nilai 7x − 8y adalah ….

A. −37
B. −5
C. 5
D. 37

Jawab:

2x − 5y = −16    |×5|   10x − 25y = −80
5x + 2y = −11 |×2|   10x +   4y = −22
                            ———————— −
                                           −29y = −58
                                           y = 2

y = 2 → 2x − 5y = −16
              2x − 5×2 = −16
              2x − 10 = −16
              2x = −6
                x = −3

∴ 7x − 8y = 7×(−3) − 8×2
= −21 − 16 = −37 (A).

Diketahui sistem persamaan linear 3x + y = −10 dan 2x + 3y = −16. Nilai dari 3x − 2y adalah ….

A. 4
B. 2
C. −2
D. −4

Jawab:

3x +   y = −10    |×3|   9x + 3y = −30
2x + 3y = −16 |×1|   2x + 3y = −16
                            ——————— −
                                           7x = −14
                                           x = −2

x = −2 → 3x + y = −10
                 3×(−2) + y = −10
             −6 + y = −10
                 y = −4

∴ 3x − 2y = 3×(−2) − 2×(−4)
= −6 + 8 = 2 (B).

Soal No. 20 tentang Aplikasi Sistem Persamaan Linear Dua Variabel

Diketahui harga 5 kg apel dan 3 kg jeruk Rp79.000,00, sedangkan harga 3 kg apel dan 2 kg jeruk Rp49.000,00. Harga 1 kg apel adalah ….

A. Rp11.000,00
B. Rp10.000,00
C. Rp9.000,00
D. Rp8.000,00

Pembahasan

Kita buat permisalan terlebih dahulu.

x : apel
y : jeruk

Selanjutnya kita buat model matematikanya dan kita selesaikan dengan cara eliminasi.

5x + 3y = 79.000    |×2|   10x + 6y = 158.000
3x + 2y = 49.000 |×3|     9x + 6y = 147.000
                            ————————— −
                                        x = 11.000

Jadi, harga 1 kg apel adalah Rp11.000,00 (A).

Soal No. 20 dari Paket dari Paket Soal yang Lain

Andik membeli 2 kelereng dan 4 gasing seharga Rp7.000,00. Kakak membeli 5 kelereng dan 7 gasing dengan harga Rp13.000,00. Harga 1 lusin kelereng adalah ….

A. Rp6.000,00
B. Rp10.000,00
C. Rp12.000,00
D. Rp1800,00

Jawab:

2x + 4y =   7.000    |×7|   14x + 28y = 49.000
5x + 7y = 13.000 |×4|   20x + 28y = 52.000
                            ————————— −
                                        6x = 3.000 (bawah − atas)
                                                        x = 500

Artkel Terkait Analisislah pentingnya unsur manajemen man

∴ 1 lusin → 12x = 12×500 = 6000 (A)

Diketahui harga 4 buah buku tulis dan 2 buah pensil Rp13.000,00. Harga 3 buah buku tulis dan sebuah pensil Rp9.000,00. Harga 5 buah buku tulis dan 2 buah pensil adalah ….

A. Rp12.500,00
B. Rp14.000,00
C. Rp15.000,00
D. Rp15.500,00

Jawab:

4x + 2y = 13.000    |×½|   2x + y = 6.500
3x +   y =   9.000 |× 1|   3x + y = 9.000
                            ——————— −
                                           x = 2.500    (bawah − atas)

x = 2.500 → 3x + y = 9.000
                   3×2.500 + y = 9.000
                   7.500 + y = 9.000
                y = 1.500

∴ 5x + 2y = 5×2.500 + 2×1.500
= 12.500 + 3.000 = 15.500 (D).

Harga 4 buku tulis dan 3 pensil adalah Rp13.500,00. Harga 3 buku tulis dan 2 pensil adalah Rp9.750,00. Harga 2 buku tulis dan 3 pensil adalah ….

A. Rp11.250,00
B. Rp10.000,00
C. Rp9.500,00
D. Rp9.000,00

Jawab:

4x + 3y = 13.500    |×2|   8x + 6y = 27.000
3x + 2y =   9.750 |×3|   9x + 6y = 29.250
                            ———————— −
                                          x = 2.250    (bawah − atas)

x = 2.250 → 3x + 2y =   9.750
                   3×2.250 + 2y = 9.750
                   6.750 + 2y = 9.750
               2y = 3.000
                       y = 1.500

∴ 2x + 3y = 2×2.250 + 3×1.500
= 4.500 + 4.500 = 9.000 (D).

Harga 3 kg mangga dan 4 kg jeruk Rp81.000,00, sedangkan harga 2 kg mangga dan 6 kg jeruk adalah Rp104.000,00. Harga 5 kg mangga dan 5 kg jeruk adalah ….

A. Rp35.000,00
B. Rp75.000,00
C. Rp110.000,00
D. Rp220.000,00

Jawab:

3x + 4y =   81.000    |×2|   6x + 8y = 162.000
2x + 6y = 104.000 |×3|   6x + 18y = 312.000
                            ————————— −
                                          10y = 150.000    (bawah − atas)
                                                      y = 15.000

y = 15.000 → 3x + 4y =   81.000
                     3x + 4×15.000 = 81.000
                     3x + 60.000 = 81.000
               3x = 21.000
                         x = 7.000

∴ 5x + 5y = 5×7.000 + 5×15.000
= 35.000 + 75.000 = 110.000 (C).

Karan membeli 3 buah gayung dan 4 buah ember seharga Rp95.000,00,sedangkan Galuh membeli 5 buah gayung dan 2 buah ember dengan harga Rp65.000,00. Harga 4 buah gayung dan 5 buah ember adalah ….

A. Rp105.000,00
B. Rp120.000,00
C. Rp125.000,00
D. Rp150.000,00

Jawab:

3x + 4y = 95.000    |×1|    3x + 4y =   95.000
5x + 2y = 65.000 |×2|   10x + 4y = 130.000
                            ————————— −
                                       7y = 35.000    (bawah − atas)
                                                     y = 5.000

y = 5.000 → 3x + 4y = 95.000
                   3x + 4×5.000 = 95.000
                     3x + 20.000 = 95.000
                   3x = 75.000
                       x = 25.000

∴ 4x + 5y = 4×25.000 + 5×5.000
= 100.000 + 25.000 = 125.000 (C).

Asri membeli 3 buah roti A dan 5 buah roti B dengan harga Rp39.000,00. Sedangkan Barkah juga membeli 1 buah roti A dan 1 buah roti B dengan harga Rp11.000,00. Jika Cantik ingin membeli 4 buah roti A dan 2 buah roti B maka jumlah uang yang harus ia bayar adalah ….

A. Rp28.000,00
B. Rp36.000,00
C. Rp38.000,00
D. Rp62.000,00

Jawab:

3x + 5y = 39.000    |×1|   3x + 5y = 39.000
x +   y = 11.000 |×3|   3x + 3y = 33.000
                            ———————— −
                                          2y = 6.000
                                                  y = 3.000

y = 3.000 → x +   y = 11.000
                   x + 3.000 = 11.000
                     x = 8.000

∴ 4x + 2y = 4×8.000 + 2×3.000
= 32.000 + 6.000 = 38.000 (C).

Simak Pembahasan Soal Matematika SMP UN 2014 selengkapnya.

Dapatkan pembahasan soal dalam file pdf di sini.

Terimakasih

Semoga Bermanfaat

Soal No. 16 tentang Grafik Fungsi Linear

Pembahasan

Soal No. 16 dari Paket Soal yang Lain

Soal No. 17 tentang Persamaan Garis Lurus

Pembahasan

Soal No. 17 dari Paket Soal yang Lain

Soal No. 18 tentang Gradien Garis Lurus

Pembahasan

Soal No. 18 dari Paket Soal yang Lain

Soal No. 19 tentang Sistem Persamaan Linear Dua Variabel

Pembahasan

Soal No. 19 dari Paket Soal yang Lain

Soal No. 20 tentang Aplikasi Sistem Persamaan Linear Dua Variabel

Pembahasan

Soal No. 20 dari Paket dari Paket Soal yang Lain

Share this:

Related posts: