pembahasan selanjutnya adalah

Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2017 Kode Naskah 157 nomor 6 sampai dengan nomor 10 tentang:
- irisan kerucut,
- suku banyak,
- geometri,
- integral, dan
- limit fungsi trigonometri.
Soal No. 6 tentang Irisan Kerucut
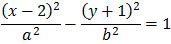
Jika asimtot hiperbola tersebut mempunyai gradien 2 maka nila b2 − a2 = ….
A. 3
B. 6
C. 9
D. 12
E. 27
Pembahasan
Kita perhatikan persamaan lingkaran dan bentuk umumnya terlebih dahulu.
x2 + y2 − 4x + 2y − 4 = 0
x2 + y2 + Ax + By + C = 0
Dengan membandingkan bentuk umumnya, diperoleh:
A = −4
B = 2
C = −4
Pusat dan jari-jari lingkaran tersebut adalah:
pusat = (−½ A, −½ B)
= (2, −1)
Jari-jari = √[¼ (A2 + B2) − C]
= √(¼ [(−4)2 + 22] − (−4))
= √9
= 3
Sekarang kita perhatikan persamaan hiperbola dan bentuk bakunya.

Berdasarkan persamaan baku tersebut, diperoleh:
Pusat = (h, k)
= (2, −1)
Ternyata lingkaran dan hiperbola mempunyai titik pusat yang sama, yaitu (2, −1). Keadaan ini dapat digambarkan sebagai berikut:

Karena hiperbola menyinggung lingkaran maka puncak hiperbola tersebut adalah (−1, −1) dan (5, −1) (lihat gambar).
Mari kita substitusikan salah satu puncak tersebut ke persamaan hiperbola, ambil saja puncak (−1, −1).

Diketahui bahwa gradien asimtot hiperbola adalah 2, sehingga:
b/a = 2
b2/a2 = 4
b2/9 = 4
b2 = 36
Dengan demikian,
b2 − a2 = 36 − 9
= 27
Jadi, nila dari b2 − a2 adalah 27 (E).
Soal No. 7 tentang Suku Banyak
A. 2x − 1
B. 3x − 2
C. 5x − 4
D. −3x + 4
E. −5x + 6

Pembahasan
Untuk menyelesaikan soal di atas, kita pahami kembali teorema sisa berikut ini:
Jika f(x) dibagi x − a maka sisanya adalah f(a)
Karena yang ditanyakan sisa pembagian p(x) oleh (x − 1)(x − 3) maka kita tentukan dulu sisa pembagian oleh (x − 1) dan (x − 3), yaitu p(1) dan p(3).
p(x) = (x − 1)q(x) + 1
p(1) = (1 − 1)q(1) + 1
= 0 + 1
= 1
p(3) = (3 − 1)q(3) + 1
= 2×5 + 1 [ingat q(3) = 5]
= 11
Misalkan sisa pembagian p(x) oleh (x − 1)(x − 3) adalah p(x) = ax + b, maka:
p(1) = a + b = 1 … (1)
p(3) = 3a + b =11 … (2)
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯ − [bawah dikurangi atas]
2a = 10
a = 5
Substitusi a = 5 ke persamaan (1).
5 + b = 1
b = 4
Dengan demikian sisa pembagian tersebut adalah:
ax + b = 5x − 4
Jadi, sisa pembagian p(x) oleh (x − 1)(x − 3) adalah 5x − 4 (C).
Soal No. 8 tentang Geometri

Luas daerah irisan kedua lingkaran adalah ….
A. 18π + 18
B. 18π − 18
C. 14π + 14
D. 14π − 15
E. 10π + 10
Pembahasan
Perhatikan daerah irisan kedua lingkaran tersebut!

Daerah irisan kedua lingkaran tersebut terdiri dari dua daerah, yaitu daerah I dan II.
Daerah I merupakan luas setengah lingkaran kecil yang berjari-jari rI = 3√2.
LI = ½ × πrI2
= ½ × π × (3√2)2
= 9π
Sedangkan daerah II merupakan tembereng dari lingkaran besar.

Tali busur AB merupakan diameter lingkaran kecil sehingga ∠AOB = 90°.
Luas daerah II merupakan pengurangan dari luas juring AOB dengan luas segitiga AOB.
LII = Lj.AOB − L.∆AOB
= (90°/360°) × πrII2 − 1/2 × rII2
= 1/4 × π × 62 − 1/2 × 62
= 9π − 18
Dengan demikian, luas daerah irisan kedua lingkaran tersebut adalah:
L = LI + LII
= 9π + 9π − 18
= 18π − 18
Jadi, luas daerah irisan kedua lingkaran adalah 18π − 18 (B).
Soal No. 9 tentang Integral
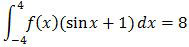
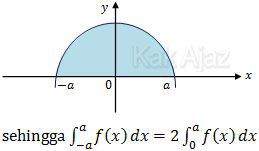
dengan f(x) fungsi genap dan
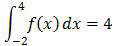
maka
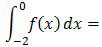
A. 0
B. 1
C. 2
D. 3
E. 4
Pembahasan
Mari kita pahami terlebih dahulu perbedaan antara fungsi genap dan fungsi ganjil!
Fungsi Genap
Jika f(x) fungsi genap maka berlaku:
- f(−a) = f(a)
- grafik f(x) dalam interval −a ≤ x ≤ a berbentuk simetris
Fungsi Ganjil
Jika f(x) fungsi ganjil maka berlaku:
- f(−a) = −f(a)
- grafik f(x) dalam interval –a ≤ x ≤ a berlawanan tanda
Nah, mari kita selesaikan soal di atas!

f(x) adalah fungsi genap dan sin x adalah fungsi ganjil sehingga f(x) sin x adalah fungsi ganjil.
Dengan demikian diperoleh:
Selanjutnya kita tuntaskan integral berikut ini.

Jadi, nilai dari integral fungsi f(x) dengan batas −2 sampai dengan 0 adalah 0 (A).
Soal No. 10 tentang Limit Fungsi Trigonometri
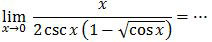
A. −2
B. −1
C. 0
D. 1
E. 2
Pembahasan
Langkah pertama kita ubah csc x menjadi 1/sin x.

Kemudian kita kalikan dengan bilangan sekawan dari 1 − √(cos x), yaitu 1 + √(cos x).

Analogi dari rumus cos 2x = 1 − 2 sin2x, diperoleh cos x = 1 − 2 sin2 ½x sehingga 1 − cos x = 2 sin2 ½x.

Limit trigonometri mendekati nol berlaku sin x = x sehingga:
Nah, sekarang tinggal memasukkan x = 0.
= 1 + √(cos 0 )
= 1 + 1
= 2
Jadi, nilai limit fungsi trigonometri tersebut adalah 2 (E).
Simak Pembahasan Soal TKD Saintek SBMPTN 2017 selengkapnya.
Nantikan, Pembahasan Matematika No. 11 – 15 TKD Saintek SBMPTN 2017 Kode Naskah 157
Dapatkan pembahasan soal dalam file pdf di sini.
Terimakasih
Semoga Bermanfaat