Pembahasan Matematika No. 11 – 15 TKD Saintek SBMPTN 2018 Kode Naskah 466

Pembahasan soal Matematika Tes Kemampuan Dasar Sains dan Teknologi (TKD Saintek) Seleksi Bersama Masuk Perguruan Tinggi Negeri (SBMPTN) tahun 2018 Kode Naskah 466 nomor 11 sampai dengan nomor 15 tentang:

• integral, 
• barisan dan deret, 
• pertidaksamaan trigonometri, 
• fungsi eksponen, serta 
• garis singgung lingkaran.

Soal No. 11 tentang Integral

Nilai

adalah ….

A.   19
B.   38
C.   57
D.   76
E.   95

Pembahasan

Bentuk integral di atas adalah integral substitusi. Cirinya, terdiri dari dua fungsi yang mana bila salah satu fungsi diturunkan akan menghabiskan fungsi yang lain.

Perhatikan bentuk integral berikut!

Fungsi pertama adalah fungsi pangkat −2 sedangkan fungsi yang kedua adalah fungsi pangkat −1. Jika fungsi pangkat −1 diturunkan akan menghabiskan fungsi pangkat −1.

Mari kita kerjakan pelan-pelan!

Integral di atas bentuknya sama dengan integral berikut:

−3∫ a^1/2da = −3 ∙ 2/3 ∙ a^3/2 + C

Ok, mari kita lanjutkan!

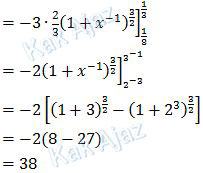
Jadi, nilai dari integral di atas adalah 38 (B).

Soal No. 12 tentang Barisan dan Deret

Pembahasan

Kita tentukan dulu anggota himpunan A dan B. Himpunan A adalah barisan aritmetika dengan suku awal 5 dan beda 3. Suku ke-100 adalah:

   a_n = a₁ + (n − 1)b
a₁₀₀ = 5 + 99 ∙ 3
        = 302

Sehingga himpunan A adalah:

A = {5, 8, 11, 14, 17, 20, 23, …, 302}

Sedangkan anggota himpunan B barisan aritmetika dengan suku awal 3 dan beda 4. Suku ke-100 adalah:

   b_n = b₁ + (n − 1)b
b₁₀₀ = 3 + 99∙4
        = 399

Sehingga himpunan B adalah:

A = {3, 7, 11, 15, 19, 23, 27, …, 399}

Dengan demikian irisan himpunan A dan B adalah:

A∩B = {11, 23, …}

Anggota irisan himpunan tersebut merupakan barisan aritmetika dengan suku awal 11 dan beda 12. Suku terakhirnya pasti kurang dari 302 (bukan 399). Sehingga banyaknya suku adalah:

                      U_n < 302
       a + (n − 1)b < 302
11 + (n − 1) ∙ 12 < 302
    11 + 12n − 12 < 302
                     12n < 303
                         n < 303/12
                         n < 25,25

Karena n adalah bilangan asli maka n = 25.

Jadi, banyaknya anggota A∩B adalah 25 (-).

Soal No. 13 tentang Pertidaksamaan Trigonometri

Pembahasan

Modal utama untuk menyelesaikan soal di atas adalah mengingat kembali dua rumus berikut:

cos⁡(90° − x) = sin ⁡x
cos 2x = 1 − 2 sin²⁡ x ⇔ 1 − cos ⁡2x = 2 sin²⁡ x

Nah, mari kita selesaikan soal di atas!

      2 cos⁡(π/2 − x) cos⁡x ≥ 1 − cos ⁡2x
                 2 sin ⁡x cos ⁡x ≥ 2 sin²⁡ x
2 sin²⁡ x − 2 sin ⁡x cos ⁡x ≤ 0
  2 sin ⁡x (sin⁡ x − cos ⁡x) ≤ 0

Pembuat nol pertidaksamaan di atas adalah:

I.   sin⁡ x = 0
           x = 0°, 180°, 360° atau
           x = 0, π, 2π

II.   sin⁡ x − cos ⁡x = 0
                   sin ⁡x = cos ⁡x
          sin⁡ x/cos ⁡x = 1
                   tan⁡ x = 1
                         x = 45°, 225° atau
                         x = π/4, 5π/4

Garis bilangan untuk pertidaksamaan tersebut adalah:

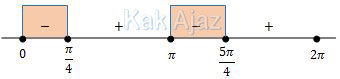
Yang memenuhi interval [π, 2π] adalah π ≤ x ≤ 5π/4 yang lazim dinotasikan dalam bentuk [π, 5π/4]. Dengan demikian diperoleh:

a = π
b = 5π/4

Sehingga

a + b = π + 5π/4
         = 4π/4 + 5π/4
         = 9π/4

Jadi, nilai a + b adalah 9π/4 (A).

Soal No. 14 tentang Fungsi Eksponen

Pembahasan

Grafik y = f(x) berada di bawah grafik y = g(x).

               f(x) < g(x)
    2^{x2 + x − 12} < 4^{2x − 7}
    2^{x2 + x − 12} < (2²)^{2x − 7}
   x² + x − 12 < 4x − 14
   x² − 3x + 2 < 0
(x − 1)(x − 2) < 0

Pembuat nol pertidaksamaannya adalah:

x = 1 atau x = 2

Karena tanda pertidaksamaannya “<” maka hasil dari pertidaksamaan tersebut berada di antara 1 dan 2.

1 < x < 2 atau (1, 2)

Sehingga diperoleh:

a = 1
b = 2

Dengan demikian:

a² + b² = 1² + 2²
             = 5

Jadi, nilai dari a² + b² adalah 5 (B).

Soal No. 15 tentang Garis Singgung Lingkaran

Pembahasan

Garis singgung lingkaran x² + y² = r² di titik (x₁, y₁) dirumuskan:

x₁x + y₁y = r²

Garis l₁ adalah garis singgung lingkaran x² + y² = 2 di titik (1,−1). Persamaan garis l₁ adalah:

1x + (−1)y = 2
         x − y = 2

Gradien garis l₁ adalah:

m₁ = −a/b
      = −1/(−1)
      = 1

Garis l₂ tegak lurus l₁ sehingga perkalian gradiennya sama dengan −1.

m₁ ∙ m₂ = −1
   1 ∙ m₂ = −1
        m₂ = −1

Garis l₂ merupakan garis singgung lingkaran x² + y² = 4 (jari-jari = 2).

      y = m₂x ± r√(m₂² + 1)
      y = −x ± 2√2
y + x = ±2√2

Berarti garis l₂ ada dua, yaitu

y + x = +2√2  dan
y + x = −2√2

Kak Ajaz ambil yang positif saja, kalau tidak ada jawabannya baru kita gunakan yang negatif.

Sekarang kita tentukan titik potong antara garis l₁ dan l₂. Bisa dengan cara eliminasi atau substitusi. Eliminasi saja, ya!

l₁ : x − y = 2
l₂ : x + y = 2√2
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  +
          2x = 2 + 2√2
            x = 1 + √2

l₁ : x − y = 2
l₂ : x + y = 2√2
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯  −
        −2y = 2 − 2√2
            y = −1 + √2
               = √2 − 1

Dengan demikian titik potongnya adalah:

(1 + √2, √2 − 1)

Jadi, titik potong garis l₁ dam l₂ adalah (1 + √2, √2 − 1) (A).

Simak Pembahasan Soal TKD Saintek SBMPTN 2018 selengkapnya.

Simak juga:
Pembahasan Matematika SBMPTN 2014
Pembahasan Matematika SBMPTN 2015
Pembahasan Matematika SBMPTN 2016
Pembahasan Matematika SBMPTN 2017
Pembahasan Matematika UTBK SBMPTN 2019

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih