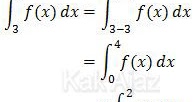Pembahasan Matematika No. 11 – 15 TKD Saintek SBMPTN 2016 Kode Naskah 225

• integral tentu, 
• aplikasi integral: luas daerah, 
• probabilitas, 
• aplikasi turunan: garis singgung kurva, dan 
• fungsi kuadrat.

Soal No. 11 tentang Integral Tentu

Pembahasan

Perhatikan pola fungsi pada soal di atas!

f(x) = f(x + 2)
f(x + 2) = f(x + 2 + 2) = f(x + 4)
f(x + 4) = f(x + 4 + 2) = f(x + 6)
f(x + 6) = f(x + 6 + 2) = f(x + 8)

Sehingga diperoleh:

f(x) = f(x + 2) = f(x + 4) = f(x + 6) = f(x + 8)

Lebih jelasnya,

f(x) = f(x + 8)

Sementara itu, disebutkan dalam soal:

∫²f(x) dx = B

Sekarang kita masuk ke pertanyaan.

₃∫⁷f(x + 8) dx = ₃∫⁷f(x) dx

Selanjutnya kita ubah batas integrasinya agar sesuai dengan data yang diketahui pada soal.

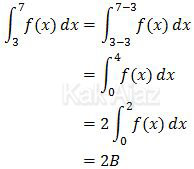
Jadi, nilai integral tentu tersebut adalah 2B (B).

Soal No. 12 tentang Aplikasi Integral: Luas Daerah

Pembahasan

Berikut ini adalah ilustrasi gambar untuk soal di atas!

D₁ adalah daerah yang dibatasi oleh garis g dan kurva f. Sedangkan D₂ adalah daerah yang dibatasi oleh kurva f, sumbu x, dan garis x = 1.

Diketahui perbandingan luas D₁ dan D₂ adalah 1 : 2.

Masukan batas integrasi x = 1 saja. Batas x = 0 tidak perlu dimasukkan karena akan menghasilkan nol. Diperoleh:

Jadi, nilai k adalah 2 (D).

Soal No. 13 tentang Probabilitas

Pembahasan

Suatu bilangan dikatakan genap apabila posisi satuan bilangan tersebut adalah angka genap.

Pada soal di atas, posisi satuan adalah c. Sedangkan c harus lebih besar dari b dan b harus lebih besar dari 3. Sehingga nilai c yang mungkin hanya 6 dan 8.

Untuk c = 6, nilai b yang mungkin adalah 4 dan 5 (ada 2 kemungkinan).

Sedangkan untuk c = 8, nilai b yang mungkin adalah 4, 5, 6, dan 7 (ada 4 kemungkinan).

Sehingga banyak susunan a dan b yang mungkin ada 6 kemungkinan.

Sementara itu, posisi a bisa diisi semua angka kecuali 0 (nol) karena nol di depan akan menghasilkan bilangan 2 digit. Nilai a yang mungkin adalah:

1, 2, 3, 4, 5, 6, 7, 8, 9 (ada 9 kemungkinan)

Dengan demikian, banyak bilangan genap yang dapat disusun adalah:

9 × 6 = 54

Jadi, banyak bilangan genap n adalah 54 (B).

Soal No. 14 tentang Aplikasi Turunan: Garis Singgung Kurva

Pembahasan

Soal di atas dapat diilustrasikan dengan gambar berikut ini!

Agar segitiga PQR sama sisi maka tiap sudutnya harus 60°. Sehingga kemiringan atau gradien garis singgung kurva (garis biru) di titik P adalah:

m = tan⁡ 60°
    =√3

Garis singgung tersebut juga merupakan turunan pertama dari kurva y = 3 − x².

m = y’
    = −2x

Nah, sekarang kita tinggal memasukkan m = √3 dan x = −a    (x di titik P).

 m = −2x
√3 = −2(−a)
2a = √3
  a = 1/2 √3

Jadi, nilai a yang membuat segitiga PQR sama sisi adalah 1/2 √3 (C).

Soal No. 15 tentang Fungsi Kuadrat

Pembahasan

Garis l menyinggung parabola y = x² − 4x + 7 di x = 5. Titik singgungnya dapat dicari dengan memasukkan x = 5 ke persamaan parabola.

y = 5² − 4 . 5 + 7
   = 12

Sehingga titik singgung antara garis l dan parabola tersebut adalah:

(x₁, y₁) = (5, 12)

Sedangkan gradien garis singgungnya merupakan turunan pertama dari fungsi parabola.

m = y’
    = 2x − 4

Dengan memasukkan x = 5 diperoleh:

m = 2∙5 − 4
    = 6

Dengan demikian, persamaan garis l dapat dicari dengan rumus:

y − y₁ = m(x − x₁)
y − 12 = 6(x − 5)
           = 6x − 30
        y = 6x − 18

Garis l juga menyinggung parabola y = p − 3(x + 2)² sehingga garis l disebut garis singgung sekutu.

Jika garis menyinggung parabola maka di titik singgungnya garis dan parabola tersebut bernilai sama dan diskriminannya sama dengan nol.

I.  y_garis = y_parabola
6x − 18 = p − 3(x + 2)²
             = p − 3(x² + 4x + 4)
             = −3x² − 12x − 12 + p
3x² + 18x − 6 − p = 0

II.                      D = 0
               b² − 4ac = 0
18² − 4∙3 (−6 − p) = 0
    324 + 72 + 12p = 0
                       12p = −396
                           p = −33

Jadi, nilai p adalah −33 (B).

Simak Pembahasan Soal TKD Saintek SBMPTN 2016 selengkapnya.

Simak juga:
Pembahasan Matematika SBMPTN 2014
Pembahasan Matematika SBMPTN 2015
Pembahasan Matematika SBMPTN 2017
Pembahasan Matematika SBMPTN 2018
Pembahasan Matematika UTBK SBMPTN 2019

Dapatkan pembahasan soal dalam file pdf  di sini.

Terimakasih